4.1.3　其他半经验模式评述

4.1.3　其他半经验模式评述

和Bagnold模式相比较,Kawamura 模式(1951)考虑了起动摩阻风速对跃移通量的影响,其模式可以表示为式(4-34):

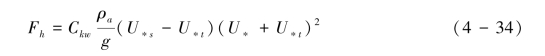
Ckw为经验常数,其最初被设置为2.78,后来的学者根据各自的实验数据对其进行了修正(见Sherman ＆amp; Li, 2011)。和其他模式相比较,Kawamura模式(1951)表现出高估跃移通量的行为(Sherman ＆amp; Li, 2011)。

Zingg (1953) 模式与Bagnold模式结构基本一致,只是粒径比率的幂指数为3/4而非后者的1/2。和其他半经验模式相比较,Zingg (1953) 模式预测结果大约低于观测结果一个数量级(Sherman ＆amp; Li, 2011)。

Owen (1964)模式表示为式(4-35):

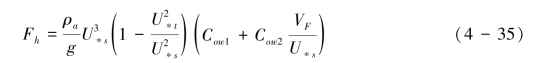
Cow1和Cow2为经验常数,分别为0.25和0.33,VF为颗粒沉降速度。Owen (1964)模式预测结果和Sørensen (2004)接近且低于Bagnold模式的预测结果(Sherman ＆amp; Li,2011)。

Kadib (1965)模式可以表述为式(4-36):

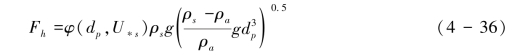
由于φ(dp,U∗s)是个非线性的隐函数,因而Kadib(1965) 模式是不易使用的。当U∗s＆lt;0.5 m·s-1时,Kadib (1965) 模式预测结果高于Bagnold模式;U∗s≥0.5 m·s-1,其预测结果低于Bagnold模式(Sherman ＆amp; Li, 2011)。

Hsu (1971) 模式与Bagnold模式结构相似,它假定跃移通量与摩阻风速的3次方成正比,与沙粒粒径和重力成反比。其预测结果和Bagnold模式相似(Sherman ＆amp; Li, 2011)。

Lettau ＆amp; Lettau (1978) 模式考虑了起动摩阻风速对跃移通量的影响,它提出了差额摩阻风速的概念(excess shear velocity),即摩阻风速与起动摩阻风速的差值。该模式可表述为式(4-37):

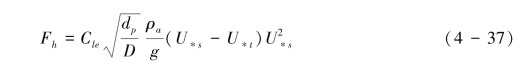
模式中Cle为6.7。按照Bagnold建模思路和Owen(1964)边界层粒载切应力的概念,跃移通量的表达式中宜采用U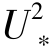∗s(s-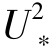t)(Shao, 2000)。Lettau ＆amp; Lettau (1978)模式预测结果与Kawamura 模式(1951)预测结果相似,它们均随摩阻风速增长是最快的(Sherman ＆amp; Li, 2011)。

White(1979)的建模思路和Bagnold(1941)有所不同,他首先假定跃移颗粒的特征距离l可表述为式(4-38):

本书著者认为,式(4-38)可以理解为右边比值与跃移特征轨迹的高度有关(从能量角度来看)而跃移水平距离与跃移高度为线性关系。

按照Owen(1964)的假定,粒载切应力可表示为τp=ρa(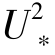s-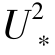t),它是沙粒轨迹形成过程中吸收湍流动量的结果,因而粒载切应力可表示为式(4-39):

式(4-39)中的mF被定义为单位时间、单位面积输送到床面的跃移颗粒的质量,其可表示为式(4-40):

此关系是基于实验观测结果(White, 1979)。

式(4-39)右边的第二项可表述为upi-upl≅Vpl, 此关系可理解为沙粒轨迹形成过程中水平动量的增加与初始垂直动量的大小成正比。这样,Vpl可表示为式(4-41):

根据式(4-38)和式(4-41),可导出式(4-42):

根据跃移通量的定义,可得到式(4-43):

由式(4-40)和式(4-43)可推导出式(4-44):

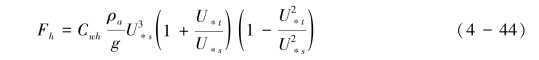
式(4-44)中的经验系数Cwh推荐为2.61(Greely, 1994)。

和Bagnold(1941)模式相比较,White(1979)模式强调了无量纲摩阻风速比对跃移输送的约束作用,但保留了前者关于跃移通量与摩阻风速3次方成正比的关系。

式(4-44)是均匀沙的跃移模式,对多粒径分布的土壤而言,前人发展了一个基于粒径对数正态分布函数的跃移通量计算的数值方案(Marticorena ＆amp; Bergametti, 1995),其可以表示为式(4-45):

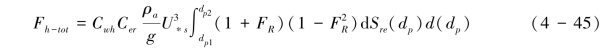
Fh-tot为混合粒径土壤的总跃移通量,Cer为可蚀性组分的覆盖度,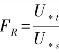,设dS(dp) 是粒径为dp的颗粒在所有颗粒中占有的面积,其可定义为式(4-46):则所有颗粒的总面积为式(4-47):

则式(4-45)中的。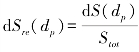

和Bagnold(1941)模式相比较,多粒径跃移通量的数值方案(Marticorena ＆amp; Bergametti, 1995)可以较好模拟多种地表类型的输沙强度(e.g.Mei, et al., 2004, 2006)。

考虑到跃移层摩阻风速计算的困难和不确定性,一个基于风洞自由风速和起动风速的跃移通量模型被提出来(Dong, et al., 2003b),它可以表述为式(4-48):

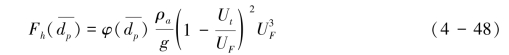
式(4-48)中的UF是指风洞边界层顶部的风速,也叫自由风速,是位于风洞中心轴线上的风速。其中。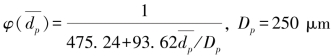

Bagnold(1941)曾建立了基于风廓线焦点风速或对数区间任意高度的风速、起动风速的跃移模式,该模式中跃移通量是风速与起动风速差值的三次方,这与Dong et al.(2003b)模式有所不同。Dong et al.(2003b)模式的优点是可以采用某个高度的风速、表土粒径来预测跃移通量,而不需要其他的复杂计算。

Sørensen(2004)采用了和Owen(1964)相同的物理假定:均一球形沙粒及相同的运动轨迹。跃移层的粒载切应力被定义为式(4-49):

式(4-49)和式(4-39)本质是一样的,m′F是单位时间单位面积跃移的移出率(dislodgement rate),当跃移达到稳恒状态时,m′F=mF,但和White(1979)不同的是,m′F的表达式不同于式(4-40)而是采用了式(4-50):

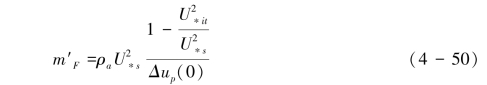
式(4-50)中的U2∗it是指沙粒碰撞起跳对应的摩阻风速的平方,Δup(0)是指在床面处沙粒水平速度增速。

式(4-49)中的Δup(z)是单个沙粒在z高度平均的水平增速,不过和White(1979)不同的是,Δup(z)是从沙粒轨迹方程来求解而非量纲分析获得。当然此轨迹方程求解也采用了一些量纲分析的假定(Sørensen,2004)。

Sørensen(2004)引入参数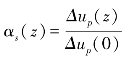,结合式(4-49),则式(4-48)可变形为式(4-51):

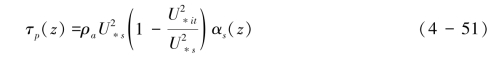
根据湍流涡黏理论的假定,可推导出式(4-52):

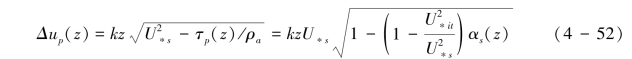
式(4-52)把沙粒水平速度的增加和湍流切应力及风速梯度联系起来,于是跃移层内风速廓线方程可表示为式(4-53):

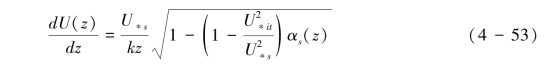
式(4-53)可近似处理为式(4-54):

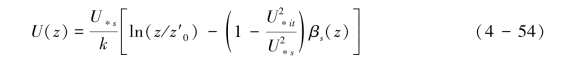
z′0为风速为零的高度,,αs(z)和βs(z)和摩阻风速轻微相关的参数,它们主要反映了沙粒吸收湍流动量的强度。

把式(4-54)插入沙粒运动轨迹方程中,可求解沙粒的平均跃距l , 结合跃移通量的定义 以及式(4-50),可推导出无量纲的跃移通量方程(4-55):

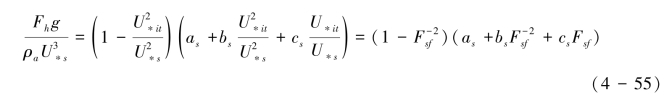
在式(4-55)中,U∗it用Shields-Bagnold公式来计算,无量纲摩阻风速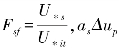(0)意味着沙粒从风廓线k-1[ln(z/z′0)-βs(z)]对应的高度出发的平均跃距,bsΔup(0)可解释为沙粒从风廓线k-1βs(z)对应高度出发的平均跃距; csΔup(0)U∗it/g 代表无气流加速作用下沙粒的平均跃距。

这里假定as,bs, cs是与摩阻风速无关的经验常数,它们与沙粒粒径及其分布特征、形状和床面颗粒堆积结构有关(Sørensen, 2004)。通过分析前人的观测数据(Iversen ＆amp; Rasmussen, 1999),Sørensen(2004)发现上述参数随着均匀沙粒径的变化而变化(见表4-1)。

表4-1　式(4-55)的经验参数随沙粒粒径的变化(根据Sørensen(2004) 数据整理 )

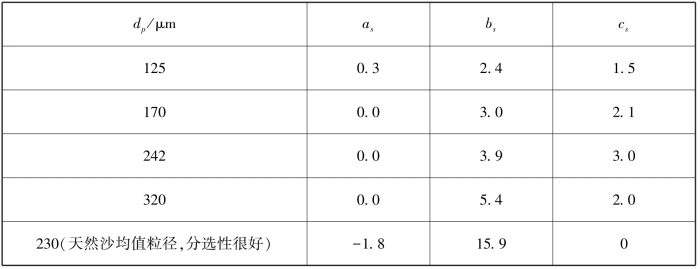
Sørensen(2004)认为as拟合结果有不确定性,它应有一个很小的数值。bs和 cs随着粒径的增加而线性增加。对天然沙跃移通量而言,上述经验参数的变化更大(见表4-1)。

和Bagnold (1941)模式相比较,后续研究(Owen, 1964; Ungar ＆amp; Haff, 1987; Sauermann, et al., 2001; Sørensen, 2004;Kok ＆amp; Renno, 2009)的重要进展是发现了无量纲跃移通量随无量纲摩阻风速变化的峰值行为(peak behaviour),即无量纲跃移通量与无量纲摩阻风速的比值不是一个仅与沙粒粒径分布有关的常数,而是随着无量纲摩阻风速先增后减的变量。新发现为理解跃移通量与摩阻风速非线性关系及发展跃移通量模式提供了新视角。Sørensen(2004)给出了跃移通量模式中经验参数的物理解释,很好地促进了人们对风沙跃移机理的理解。同时可看到,与Sørensen(2004)跃移模式结构相近的模式之间仍存在差异,这与相关假定和推理过程的差异有关。

Sørensen(2004)认为他的模式可能在高摩阻风速下不准确,这是因为在高摩阻风速下,空中碰撞加剧会限制跃移通量。不仅如此,在高摩阻风速下,湍流对沙粒轨迹的影响更加复杂。模式中经验系数as,bs, cs被假定为不依赖于摩阻风速的常数,但此假定与沙粒起跳速度的概率分布有关。若起跳速度概率分布特征与摩阻风速无关,则此假定成立。然而一些学者观点与此相左(Owen, 1964; Anderson ＆amp; Hallet, 1986)。近年来起跳速度的实验观测结果表明(e.g.Dong, et al., 2002a; Huang, et al., 2006; Kang, et al., 2008),摩阻风速虽然不能影响起跳速度概率分布的形式,但会影响概率分布模式中的经验参数,这意味着摩阻风速对起跳速度的概率分布是有明显影响的,因而as,bs,cs必然依赖于摩阻风速的变化。

野外实验观测表明(Sherman ＆amp; Li, 2011),和Bagnold模式相比较,在中等和高摩阻风速下Sørensen(2004)会低估跃移通量。最近的数值研究和观测数据的(Iversen ＆amp; Rasmussen, 1999)分析表明(Kok ＆amp; Renno, 2009),Sørensen(2004)模式和同类的模式均显著地低估了跃移通量。尽管如此,和其他半经验模式相比较,Sørensen(2004)模式具有更丰富的物理机理和可解释性,且能预测跃移通量的峰值行为,尽管峰值现象产生的原因还没有得到很好地解释。

综上所述,半定量跃移通量模式可分为3类:①Bagnold型,该类模型模拟的跃移通量是摩阻风速的3次方,无量刚跃移通量正比于无量刚摩阻风速线性函数;②Sørensen(2004)型,其模拟的无量纲跃移通量是无量纲摩阻风速的非线性函数,当无量纲摩阻风速为2.0时无量纲跃移通量达到峰值,但峰值行为产生的原因还不明确;③基于风速和起动风速的跃移模式(Bagnold,1941; Dong, et al., 2003)。这些形式多样由不同实测数据支撑的跃移通量模式之间的分歧,暗示了目前研究对跃移过程理解还很有限。未来研究应充分地利用室内与野外观测、数值计算等手段从多个角度精细地剖解跃移过程,为发展具有普适化的模型奠定基础。

所有半经验模型遇到最大的挑战是如何理解高时间分辨下跃移强度与湍性风风况的关系,下面对此问题进行简要的讨论和分析。