2.2.4 DPM模型 (Alfaro ＆amp; Gomes, 2001)
DPM粉尘释放模型是对前人粉尘释放模型改进而形成的(Marticorena ＆amp; Bergametti,1995; Marticorena, et al., 1997)。在White (1979) 跃移通量模式的基础上,前人考虑了所有粒级的可蚀性土壤微团聚体对跃移通量的贡献,建立了改进的跃移通量模型(Marticorena ＆amp; Bergametti, 1995; Marticorena, et al., 1997)。根据野外实验观测的冲击作用效率的数据(Gillette,1979)和风洞实验观测的跃移冲击作用实验的结果(Shao, et al.,1993),Marticorena研究小组假定冲击作用效率 (跃移通量与粉尘通量之比) 是土壤黏粒含量的指数函数并依此建立了粉尘通量模式。
Alfaro et al.(1997, 1998) 通过风洞冲击作用实验发现, 随着摩阻风速的增大,释放的粉尘粒度分布呈现变小的趋势;粉尘的粒度分布可表示为3个对数正态群体,对应的中值粒径分别为1.5 μm、6.7 μm和14 μm,随着摩阻风速的增加,细颗粒群体的比例增加;假定跃移颗粒动能全部用来克服粉尘颗粒之间的结合能且结合能随粉尘粒径的减小而增加,据此模拟了3个对数正态分布群体的结合能。这样就可以把粉尘释放通量和粉尘粒度分布及摩阻风速联系起来,建立了基于跃移冲击作用效率(主要取决于跃移颗粒的动能和粉尘颗粒的结合能)的粉尘释放模式即DPM模式(Alfaro ＆amp; Gomes, 2001)。该模式基本上否定Marticorena ＆amp; Bergametti(1995)模式关于粉尘释放强度依赖于土壤黏粒含量的观点。
DPM模型(Alfaro ＆amp; Gomes, 2001) 可表示为式(2-9)~式(2-11):
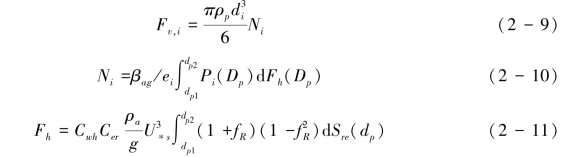
式(2-9)是粉尘释放质量通量方程,di代表了3个对数正态分布群体的粉尘颗粒的中值粒径;式(2-10)是粉尘个数通量方程,其中βag=16300 cm·s-2,为比例系数,ei为3个对数正态分布群体粉尘颗粒的结合能,Pi(Dp)是跃移颗粒动能在3个对数正态分布群体粉尘颗粒之间的分配比例,其获得的动能决定了粉尘颗粒的粒度分布和个数通量;式(2-11) 为跃移通量方程,Fh为混合粒径土壤的跃移通量,Cer为可蚀性组分的覆盖度,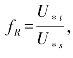
U∗和U∗t分别为摩阻风速和起动摩阻风速,Cwh为经验常数可取2.61,Dp为土壤可蚀性组分的颗粒直径(＆lt;2000 μm),
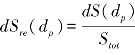,是粒径为Dp的颗粒占整个颗粒表面面积的相对比例,它取决于土壤可蚀性组分的粒度分布特征。
比较邵亚平模型和DPM模型可看出,二者既有共性也存在明显的差异:从共性来看,两模型都模拟了跃移冲击作用对粉尘释放的贡献,都分别由跃移通量模块和冲击作用模块组成,所采用的跃移通量方程、经验参数及输出结果均是相似的。
从差异性来看,土壤颗粒之间结合能是模拟粉尘释放的重要参数,而这2个模型在描述粉尘结合能有着明显的差异,邵亚平模型假定粉尘颗粒结合能与粉尘颗粒直径的平方成正比,而DPM模型假设粉尘颗粒的结合能与颗粒直径成反比;邵亚平模型把结合能表示为粉尘粒度分布的随机变量,而DPM模型把粉尘粒度分布模拟为3个对数正态群体的组合,每个群体分别有相应的中值粒径、标准偏差和结合能,结合能设为3个定值。由于目前还不能完全从理论上推导或者从实验上直接测定粉尘颗粒的结合能,因而很难判断究竟哪一种结合能模式更能反映实际情况。大体来看,邵亚平模型的结合能模式可能适合粗粉尘颗粒,而DPM模型的结合能模式可能更适合＆lt;20 μm的粉尘颗粒。
从描述粉尘释放的物理机制来看,邵亚平模型描述的粉尘释放机制更细致和全面,其是从跃移冲击作用产生的弹坑体积和土壤粒度分布的变化去考虑粉尘释放强度,是一个依据跃移颗粒能量分布的粉尘释放模式。
这两个模型在输入参数上也存在一些差别,特别是土壤粒度分布参数的定义有所差异。邵亚平模型采用了湿分散的分析方法(McTainsh, et al., 1997),并根据测定的最大扩散条件和最小扩散条件下土壤粒度分布参数来表示粉尘释放前后土壤粒度分布的变化;DPM模型采用干筛分析方法,并通过对数正态分布函数拟合观测数据来表征表土微团聚体的粒度分布特征(e.g.Chatenet, et al., 1996)。这两类土壤粒度分布的测试和模拟方法在模拟粉尘释放过程中各有优缺点,邵亚平模型采用的方法能揭示粉尘释放与土壤粒度变化的关系,但采用湿分散方法与风蚀导致的土壤团聚体分散是有差距的;DPM模型采用的干筛分析方法虽然和风蚀过程接近,且能较好反映土壤团聚体粒度分布对起动摩阻风速的影响,但没有考虑风蚀前后土壤团聚体粒度变化对粉尘释放的影响,也是不够完善的。
DPM模型得到了野外原位观测的验证和校正(Rajot, et al, 1996, 2003; Gomes, et al, 2003a, b; Mei, et al., 2006),是目前相对成熟的模型。