3.4 目前应力分解模式比较分析
粗糙元的空气动力学特征对跃移起动的影响机制主要用应力分配理论来说明,即气流在经过粗糙元覆盖地表时风应力会在光滑地表和粗糙元之间的分配,粗糙元通过吸收部分风动量而起到控制跃移起动和提高起动摩阻风速的作用。常用光滑地表与粗糙元覆盖地表的起动摩阻风速之比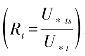
来反映应力分配关系。
自20世纪30年代Schliting提出流体应力分配的基本框架以来, 研究人员开展了一系列实验研究和理论分析,取得了许多重要认识和积累了重要的科学数据。应力分配实验研究主要通过2个途径开展工作:①通过直接测定光滑地表和粗糙元覆盖地表的风剪切应力或阻力大小来研究应力分配与粗糙元密度、结构参数(底面积与迎风面积之比σ,方向比率AR)和单个粗糙元阻力系数或者粗糙元总阻力系数的关系(Marshall,1971; Lee＆amp; Soliman, 1977; Gillette, et al., 1989; Musick,et al., 1996; Wolfe ＆amp; Nickling, 1996;Wyatt ＆amp; Nickling, 1997; Gillies, et al., 2000, 2002; Crawley ＆amp; Nickling, 2003)。②通过测定研究粗糙元和光滑地表的空气动力学粗糙度来研究粗糙元对应力分配和起动摩阻风速的影响(Alfaro ＆amp; Gomes, 1995; Lancaster, 2004; MacKinnon, et al., 2004)。这就形成了2类应力分配的模式,即基于阻力系数的模式(Raupach, 1992; Raupach ＆amp; Gillette, 1993)和基于空气动力学粗糙度的模式(Marticorena ＆amp; Bergrametti, 1995; Marticorena, et al.,1997;Alfaro ＆amp; Gomes, 1995)。前者基于阻力系数及应力直接测定数据+量纲分析而来(简称Raupach模式),后者是从双边界层的空气动力学粗糙度+量纲分析来表征粗糙元来理解应力分配机理,分别称为MB模式(Marticorena ＆amp; Bergrametti, 1995; Marticorena, et al., 1997)、SL模式(Alfaro ＆amp; Gomes, 1995)、Raupach模式和Marticorena模式。Raupach模式可表述为式(3-40),MB模式可表述为式(3-41):
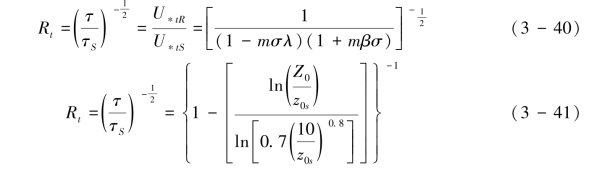
其中,U∗t r是粗糙元覆盖地表的起动摩阻风速;U∗tS是光滑裸露地表的起动摩阻风速;σ是粗糙元的底面积与迎风面积之比;m是经验常数,代表湍流剪切力分布的不均一性;β是分配在单个粗糙元上阻力系数与光滑地表阻力系数之比;λ是粗糙元的密度;Z0是植被覆盖地表的空气动力学粗糙度;Z0S光滑裸露地表的空气动力学粗糙度。
MB模式和SL模式均是在双边界层理论的基础上发展起来的(Arya, 1975)。
根据Arya的应力分配理论(Arya, 1975):气流被地表覆盖的粗糙元分割成4个区域,其中在粗糙元上方和粗糙元之间的一定距离内形成了发育良好内边界层和外边界层,中性条件下内边层和外边界层的风廓线服从对数法则,于是可以把应力分配模式表示为式(3-42):
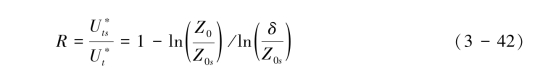
根据Elloit的研究,式(3-42)可变化为式(3-43):
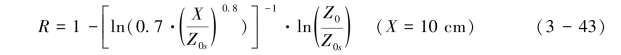
Alfaro ＆amp; Gomes(1995)认为MB模式没有考虑Z0s的影响,根据风洞实验的结果,得到简化的应力分配模式为式(3-44):
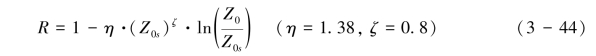
MB模式和SL模式共同特点是应力分配系数仅被表示为光滑地表的空气动力学粗糙度Z0s和粗糙床面空气动力学粗糙度Z0的函数,而相关研究表明应力分配系数不但与粗糙元密度(直接影响空气动力学粗糙度)有关,也受到粗糙元与地表阻力系数比影响。对天然植被而言,由于枝叶之间的孔隙率(porosity)的存在,它们与形状和大小相似的致密粗糙元(如圆柱体、球体和和四面体)的阻力系数显著不同,前者的阻力系数明显地大于后者,而且植被的阻力系数随着雷诺数的增加而增加,这表明在粗糙元密度一定的情况下,具有一定间隙率柔性粗糙元(如天然植被)的应力分配系数大于致密的粗糙元。
尽管考虑孔隙率对空气动力学粗糙度的影响,但不同研究者结论不完全一致。(Minvielle, et al., 2003; 梅凡民等,2012)
同样地,由于目前模型不能反映粗糙元空间分布的不均匀性对空气动力学粗糙度的影响,以空气动力学粗糙度为参数的MB模式和SL模式也不能反映粗糙元空间分布不均对应力分配的影响。
模式的改进可以从2个途径入手:一是利用风洞实验通过改进目前的空气动力学粗糙度模型使其能够反映粗糙元孔隙率和粗糙元空间分布不均对空气动力学粗糙度的影响,进而反映粗糙元孔隙率和粗糙元空间分布不均对应力分配的影响;二是利用风洞实验通过调整应力分配模型中的经验常数来反映粗糙元孔隙率和粗糙元空间分布不均对应力分配的影响,这个思路最近被MacKinnon et al.(2004) 提到,但MB模式和SL分配模式的经验常数如何变化还有待于实验研究的结果。
图3-39表明MB模式和SL模式预测的应力分配系数具有明显差异。在Z0s, Z0 相同情况下,MB模式预测的应力分配系数明显地小于SL模式的预测值;在Z0相同情况下,MB模式预测的应力分配系数随着Z0s的增大而增大,而SL模式呈现完全相反的趋势,从实验结果来看(King, et al., 2005; MacKinnon, et al., 2004),SL模式较符合应力分配机理。
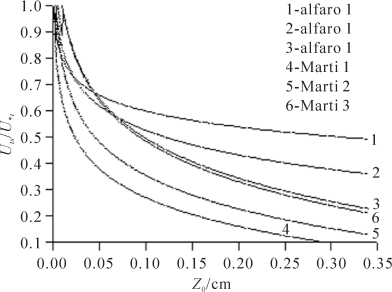
图3-39 MB和 SL模式预测的应力分配系数(alfaro 1和Marti 1对应的Z0s=0.001 cm, alfaro 2和Marti 2对应的Z0s=0.002 cm, alfaro3和Marti3对应的Z0s=0.005 cm.)(梅凡民等,2006)
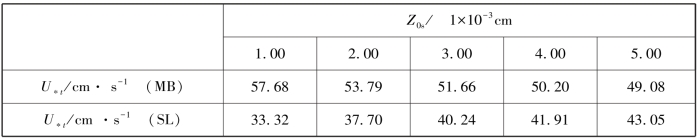
MB模式和SL模式预测的应力分配系数和起动摩阻风速表明(见表3-10),在Z0=0.05 cm, Z0s在0.001~0.005 cm之间的情况下,MB模式预测的起动摩阻风速从57.68 cm·s-1下降到49.08 cm·s-1,SL模式预测的起动摩阻风速从33.32 cm·s-1上升到43.05 cm s-1,它们不但在相同条件下预测的起动摩阻风速差异明显,而且MB模式预测数值随着Z0s增大而减小,这不符合应力分配的机制,需要通过实验重新调整MB模式中起动摩阻风速与Z0s的关系。
表3-10 敏感性试验-模式预测起动摩阻风速U∗
t随Z0s的变化(Z0=0.05 cm)(梅凡民等,2006)
MB模式和SL模式预测结果差异可能与经验常数的取值有关。鉴于应力分配过程是非线性过程,针对不同数量级的Z0,Z0s来选择不同经验常数,这能更好地反映空气动力学粗糙度对应力分配的影响(SL模式中的经验常数为实验观测的平均值),也可能减小这2个模式的差异,使它们从不同方面反映应力分配的规律。目前风洞实验还不能解决这个问题,因而有必要开展系统的风洞实验研究。
针对地表同时存在2类粗糙元的情况下(植被和砾石共存情况下)Marticorena et al.(1997) 提出了双应力分配模式:
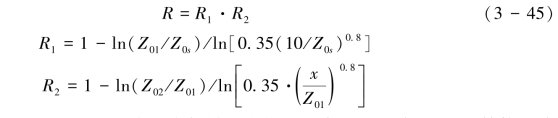
式(3-45)中的x=3/d1-2,d1-2为两个粗糙元之间的距离。鉴于式(3-45)结构和式(3-43)相似,双应力分配模式也需要通过实验进行校正。
Alfaro＆amp; Gomes (1995) 和Marticrena et al(1997)都认为当Z0＆gt;0.1 cm, 起动摩阻风速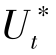
＆gt;100 cm·s-1,从敏感性试验来看(见图3-39),当Z0在0.15~0.35 cm之间能够有效地控制风蚀。风洞和野外的风蚀实验结果对这个限制条件提出了质疑:Buckley(1987),凌裕泉等(2003)的风洞实验表明对10~12 cm的植物模型,在覆盖率37%左右时,细沙输沙率才接近为零,而推测这些实验中的Z0约在0.5~0.6 cm左右(根据MB模式计算),这与前人的风洞实验的结果基本一致(董治宝等,1996);砾质戈壁达到空气动力学稳定状态的Z0约在0.2~0.6 cm,暗示了砾石覆盖的风蚀上限对应的Z0在0.2~0.6 cm(Dong,et al., 2002);高度在0.8~1.2 m的灌丛覆盖的沙质地表风蚀率的观测数据显示(黄富祥等, 2001),植被覆盖率在40%~50%才能有效降低风蚀率(Z0约在4~6 cm),这与Wasson＆amp; Nanninga(1986)的研究结论相似。Lancaster ＆amp; Baas(1998)野外实验测定的Z0分别为0.1,0.3,1,1.5 cm,对应的起动摩阻风速0.42,0.45,0.75,0.80 m·s-1。Lancaster(2004)野外观测表明应力分配系数R在0.2~0.6之间,而Z0在10-3~ 5 cm之间。上述观测实验表明MB模式和SL模式均高估了Z0对应力分配的影响,需要通过系统实验研究来重新校正,以更好地用于模拟粉尘释放强度。
Lancaster(2004)认为MB模式可能适合描述粗糙元密度较小情况下的应力分配(λ＆lt;0.05),对预测粗糙元密度λ＆gt;0.05的应力分配和起动摩阻风速是不合适的;MacKinnonet al.(2004)则提出通过调整MB模式中经验常数X以反映粗糙元密度较大情形下的应力分配。前人这些论述对改进MB模式和SL模式提供了重要的参考。