3.3.2 风廓线的拟合方法对空气动力学粗糙度的影响
3.3.2.1 分段拟合方法及空气动力学粗糙度意义分析
首先,根据风廓线的转折特征来确定风廓线分析的转折段,这里以粗糙元高度为100 mm、侧影盖度为0.126的床面为例,说明确定对数风廓线转折段的方法和拟合效果(见图3-12及表3-4)。从对数高度-风速廓线图确定了10 mm以下为非对数区域,初步确定0.1~0.6 H,0.6~2 H,2~5 H为3个转折段,然后把这几个转折段向上或向下延伸,通过比较拟合的相关系数和残差的变化最终确定风廓线转折段(见表3-4)。如0.1~0.6 H转折段向上延伸到0.1~2 H,发现后者相关系数下降到0.89,残差增大到2.4左右,说明前者风廓线更符合对数律,为最佳转折段。同样地0.6~2 H和2~5 H转折段向上或向下延伸,均出现相关系数下降和残差增大趋势,且R2≤0.98,可以认为这两个转折段向上、下延伸后不再符合对数律。
其次,根据风廓线的转折段来确定粗糙床面边界层分区、垂向差异及物理意义。
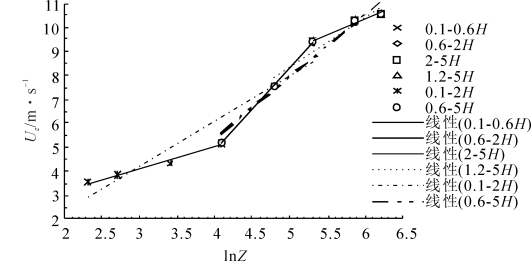
图3-12 22号床面对数风廓线转折段的拟合效果比较(梅凡民等, 2010)
表3-4 22号床面对数风廓线转折段的相关系数(R2)与残差(Q)(梅凡民等, 2010)
1)细高粗糙元风速廓线转折特征
粗糙元高度为20 mm的5组床面风廓线分别在Z=0.15 H(或Z=0.3 H)、Z=0.5 H(或Z=0.75 H)、Z=3 H(Z=6 H或Z=10 H)发生转折并形成3~4个转折段(见图3-13(a),表3-5),其中自床面向上依次为0.15 H≤Z≤0.5 H(或0.3 H≤Z≤0.75 H)、0.3 H≤Z≤3 H(或0.5 H≤Z≤6 H,或0.75 H≤Z≤6 H,或0.5 H≤Z≤10 H)等风廓线转折段符合对数律,中间转折段0.3 H≤Z≤3 H(或0.5 H≤Z≤6 H,或0.75 H≤Z≤6 H,或0.5 H≤Z≤10 H)的风速梯度最大。随着侧影盖度增加风廓线转折点呈现向高处调整的趋势。粗糙元高度为60 mm的5组床面风廓线分别在Z=0.2 H、Z=0.5 H及 Z=2 H(或Z=3.3 H)发生转折并形成4个转折段,其中0.15 H≤Z≤0.5 H(或0.3 H≤Z≤0.75 H)、0.3 H≤Z≤3.3 H和Z＆gt;3.3 H等3个转折段符合对数律,其中转折段0.3 H≤Z≤3.3 H风速梯度最大(见图3-13(b)、表3-5)。粗糙元高度为100 mm的5组床面风廓线均在Z=0.1 H和Z=0.6 H及 Z=2 H(或Z=3.5 H)出现转折并形成4个转折段(见图3-13(c)、表3-5),Z≥0.1 H的3个转折段均符合对数律,其中在0.6 H≤Z≤2 H风速梯度最大。
有趣的是,对所有细高粗糙元而言,符合对数律且风速梯度最大转折段对应的转折点为Z=0.5 H(Z=0.6 H或Z=0.75 H),与Jackson(1981)估计的粗糙床面零平面位移高度D接近(D≅0.7 H),说明该转折点正好位于零平面位移高度附近。
从Lee ＆amp; Soliman(1977)实验数据可以看到风廓线也存在4个转折段,其中0.3 H≤Z≤0.6 H和0.6 H≤Z≤1.5 H转折段风廓线符合对数律,前者较小的风速梯度可能代表了粗糙元之间光滑地表气流特征,而后者加风速梯度主要反映了粗糙元覆盖地表之上的内边界层的特征,本文关于细高粗糙元的风廓线转折特征与Lee ＆amp; Soliman有相似的趋势,但本文风廓线转折特征更加复杂,如风速梯度最大的转折段(0.6 H≤Z≤3.5 H)随着粗糙元高度和密度的增加向高处上移。相似条件下风洞观测的砾石床面和直立植被模型床面的风廓线特征也存在3~4转折段(Dong, et al., 2001),与本文风廓线转折特征有相似趋势,特别是植被覆盖床面风廓线转折特征,与本文数据有明显相似性。本文细高粗糙元风廓线的转折特征与Lee ＆amp; Soliman(1977)研究相似,而与O′Loughlin ＆amp; Annambhotla(1969)、Raupach(1980)、Raupach et al.(1996)以及Brunet et al.(1994)等研究结果有明显区别,后者均发现速度廓线大致在Z=H处形成2个转折段。上述差异可能与粗糙元的形状、高度、密度、粗糙元排列方式等因素有关。
2)粗矮粗糙元和孔隙粗糙元风速廓线转折特征
高度为10 mm的粗矮粗糙元覆盖床面的风廓线转折特征很复杂,仅在1.5 H≤Z≤35 H转折段风廓线符合对数律(见图3-13d、表3-5)。随着粗糙元高度、侧影盖度和方向比率的增加,床面风廓线中符合对数律的转折段约在1.2 H≤Z≤6 H之间。与细高粗糙元不同,粗矮粗糙元覆盖床面的风廓线虽然也存在多个转折段,但是仅在粗糙元顶端以上的风廓线才符合对数律。对比粗糙元高度、侧影高度、高度与间距比和方向比率等参数来看,粗矮与细高粗糙元覆盖床面最显著差异在于方向比率,前者方向比率在0.4~1.25之间,而后者在4~20之间,可能因为粗矮形状单个粗糙元背后的尾涡厚度比细高粗糙元大,而使得仅在粗糙元高度以上的风廓线遵循对数律。本文中粗矮粗糙元与Raupach(1980)实验所用粗糙元的方向比率接近,风廓线转折特征相似。较强尾涡发育使得粗矮粗糙元高度以下平均风速低于细高粗糙元。
孔隙粗糙元的风廓线转折特征与细高粗糙元相似,也存在3~4个转折段,风廓线符合对数律的转折段有2~3个,0.5 H≤Z≤4 H(或0.6 H≤Z≤2.4 H)之间的风速梯度最大(见图3-13e、表3-5)。高度为30 mm的3组床面与高度50 mm的3组粗糙元床面的风廓线转折特征有一定差异,但高度相同而孔隙度不同的3组床面风廓线转折特征相似,说明粗糙元高度比孔隙度能更明显地影响风廓线的转折特征。和密实粗矮粗糙元相比较,孔隙粗糙元的透风效应在一定程度上抑制了粗糙元背后的尾涡发育,使得粗糙元高度以下还存在对数风廓线区间。
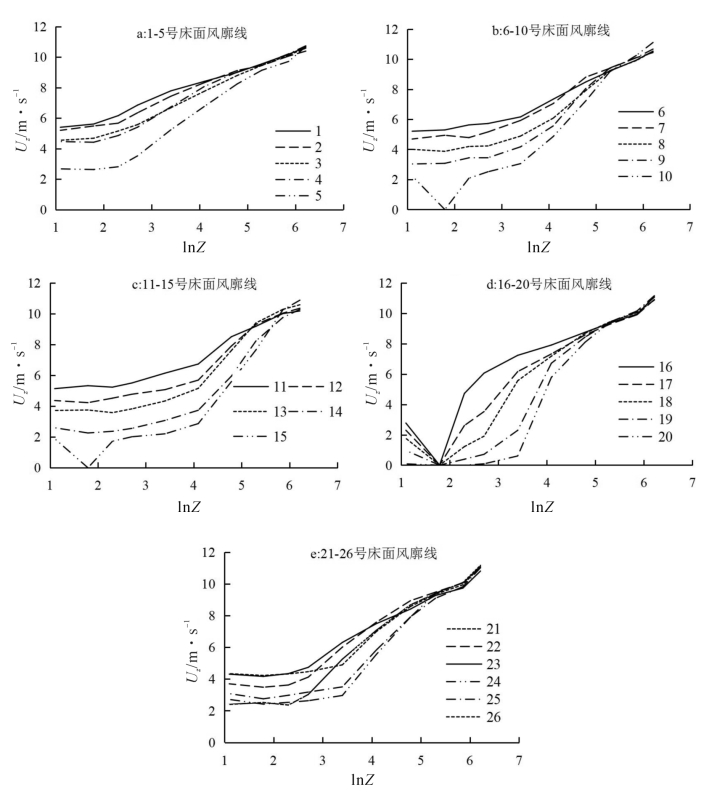
图3-13 不同粗糙床面的风廓线转折特征(梅凡民等, 2010)
总之,细高粗糙元和孔隙粗糙元覆盖床面的风廓线均有3~4个转折段,其中符合对数律有2~3个转折段,而0.5 H≤Z≤4 H的风速梯度最大,粗矮粗糙元的风廓线受单个粗糙元背后尾涡的影响,风廓线转折复杂,Z≥1.2 H风廓线符合对数律。风廓线转折特征主要受到粗糙元方向比率、高度、密度和孔隙度等因素的综合影响,但前3个因素所起作用更大。
3)粗糙床面湍流边界层垂直分化与空气动力学粗糙度的关系
根据粗糙床面风廓线转折特征、对数风廓线转折段风速梯度与床面粗糙元的形状参数和分布参数之间关系,并结合粗糙床面湍流边界层的理论,本文所研究床面湍流边界层可以分为以下几个区域:
近壁区-尾涡区:近壁区受流体黏性力的影响风速廓线偏离对数律,尾涡区受单个粗糙元背后尾涡发育的影响,风廓线也偏离对数律,由于该区域观测点很少,因此把它们放在一起讨论。对15组细高粗糙元覆盖床面而言,近壁区与尾涡区的厚度约为距地表3~10 mm左右,随着粗糙元高度和侧影盖度关系增大该区域厚度略有增加(见表3-5)。6组孔隙粗糙元覆盖床面,其近壁区-尾涡区厚度分别为10 mm 和15 mm,其中粗糙元高度为50 mm的3组床面由于存在明显过渡区域(见后讨论)它们的厚度减小为10 mm。5组粗矮粗糙元的近壁区与尾涡区,其厚度约15~60 mm之间,尾涡区厚度随粗糙元高度和侧影盖度增加而显著地增加。总体看来,近壁区-尾涡区厚度受粗糙元方向比率显著,且密实粗糙元和孔隙粗糙元差异明显。本文与Raupach(1980)及Raupach et al.(1996)数据均表明,粗矮粗糙元尾涡区厚度较大,且尾涡区厚度与粗糙元高度相当。细高粗糙元尾涡区约在粗糙元高度以下的1/10~1/2H之间。孔隙粗糙元的孔隙度增加会显著减小尾涡区的厚度。
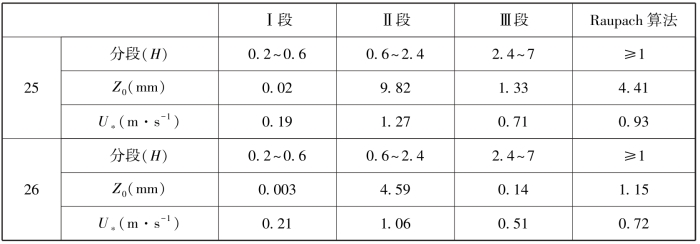
表3-5 符合对数律的风廓线转折段对应的Z0、U∗
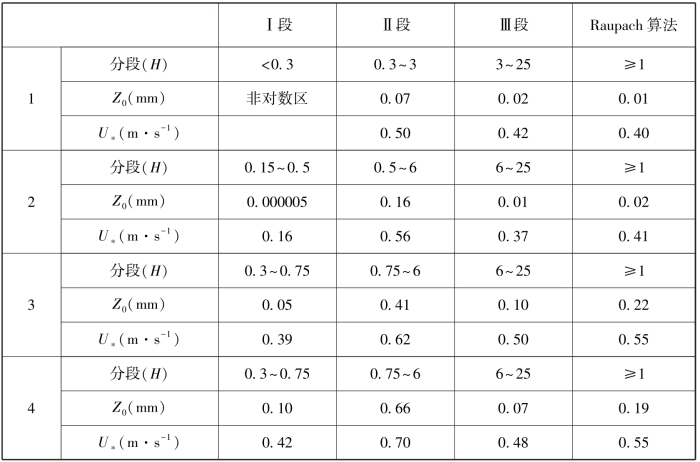
续表
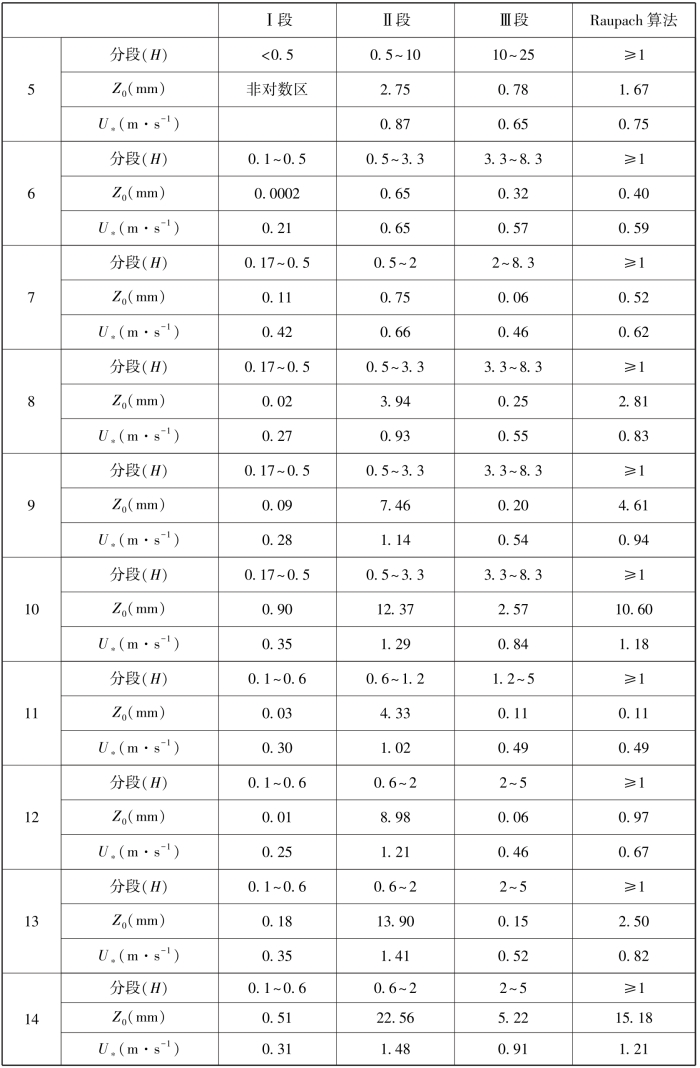
续表
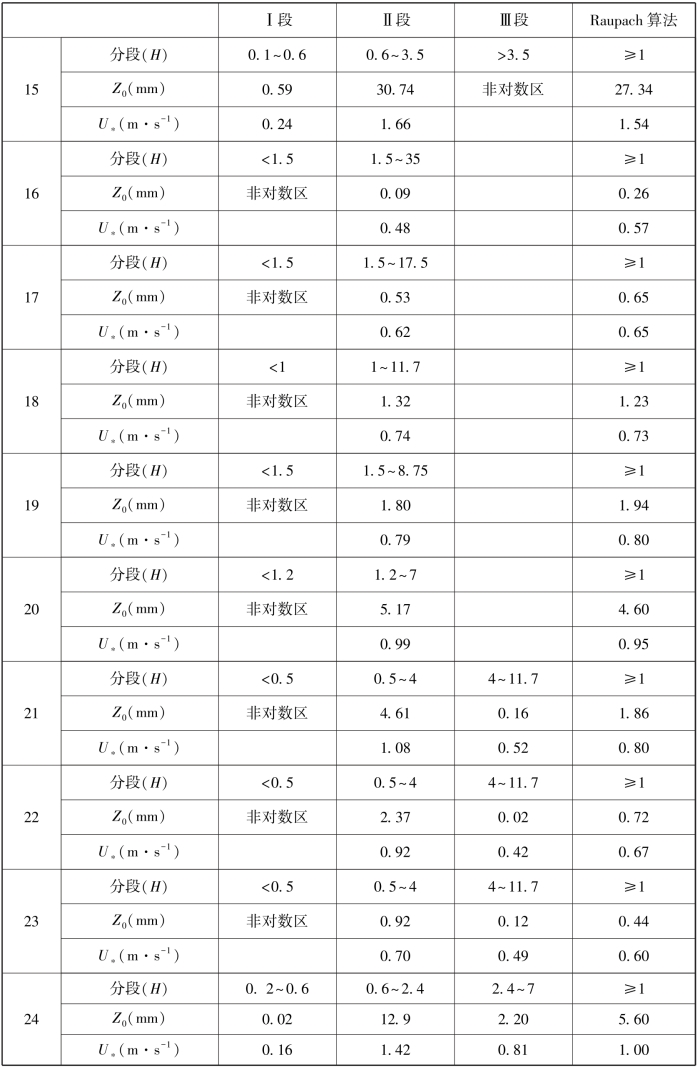
续表
内边界层:按照Eillot (1958)、Rao (1974) 等分析,当气流从空气动力学粗糙度为Z′0的光滑床面流经空气动力学粗糙度为Z0的粗糙床面时,上风向气流与Z0床面相互作用并逐渐分化为内边界层和外边界层,且内外边界层风廓线均符合对数律,前者风廓线特征与Z0有关(反映了所有粗糙元对气流阻力特征),而后者风廓线特征主要与Z′0有关。细高粗糙元和孔隙粗糙元的风廓线符合对数律的转折段有2~3个,其中风速梯度最大的对数廓线转折段代表了内边界层的空气动力学特征,反映了床面所有粗糙元对气流的阻力特征。而该区域以上风速梯度减小说明整个粗糙元对气流影响程度减弱。从内边层的发育过程来看,当气流从上风向光滑床面流经粗糙床面,内边界层风速梯度必然高于外边界层并在垂直方向上分化为内外边界层。15组细高粗糙元和6组孔隙粗糙元覆盖床面的内边界层约在1/2至几倍粗糙元高度,且随着高度和侧影盖度增加内边界层范围有向上延伸趋势,说明粗糙元对气流影响范围增大,内边界层范围似乎与粗糙元孔隙度关系不大。细高粗糙元和孔隙粗糙元内边层的范围与Lee ＆amp; Soliman(1977)研究一致。粗矮粗糙元的内边界层约在1~6倍粗糙元高度,与Raupach(1980)及Raupach et al.(1996)的研究结论相似,且没有出现过渡区域。
过渡区域:内边界层以下或以上对数风廓线转折段可以看作是内边界层与近壁-尾涡区、内边界层与外边界层的过渡区域,从正则化空气动力学粗糙度(Z0/h)随侧影盖度的变化趋势可以反映粗糙床面湍流内边界层与过渡区空气动力学性质的差异(见图3-14)。对λ＆lt;0.1时细高粗糙元床面而言,湍流内边界层的正则化空气动力学粗糙度随着侧影盖度的增加而急剧增加(在10-3~10-1之间),而当λ＆gt;0.1时,正则化空气动力学粗糙度随着侧影盖度增加的幅度减小。内边界层以下的对数区,其正则化的空气动力学粗糙度虽然也存在随侧影盖度增加而增加趋势,但同时还存在非常大波动(在10-6~10-2之间),说明该区域气流同时受到单个粗糙元尾涡和整个粗糙元的影响,其空气动力学性质既不同于粗糙床面也不同于尾涡区而介于二者之间具有过渡特征;相似地,内边界层以上对数区,其正则化空气动力学粗糙度随着侧影盖度的增加也存在显著地波动变化,说明该层气流性质同时受整个床面粗糙元和上风向气流空气动力学性质的影响,气流性质也具有过渡特征。细高粗糙元在高度和侧影盖度很大情况下,内边界层与其以上过渡区域及内边界层合并(如NO15)。同样地,孔隙粗糙元内边界层以下或以上也存在过渡区域。粗矮粗糙元覆盖床面的湍流边界层没有出现过渡区域。
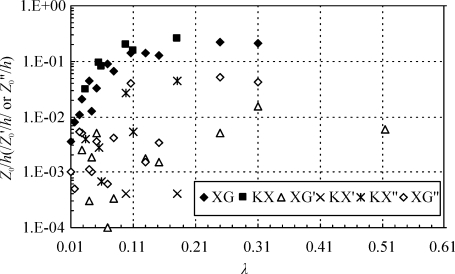
图3-14 粗糙床面湍流边界层正则化空气动力学粗糙度(Z0/h)随侧影高度(λ)变化
XG, XG′, XG″, 分别代表细高粗糙元内边界层、内边界层以下对数区、内边界层以上对数区的数据。KX, KX′,KX″,分别代表孔隙粗糙元内边界层、内边界层以下对数区、内边界层以上对数区数据(梅凡民等,2010)。
细高粗糙元覆盖床面内边界层空气动力学粗糙度比内边层以上或以下对数区域的空气动力学粗糙度高几倍到1个数量级(见表3-5)。高度为20 mm的5组粗糙床面,随着侧影盖度从0.007增加到0.1,内边界层的空气动力学粗糙度从0.07 mm增加到2.35 mm;内边界层以上过渡层的空气动力学粗糙度在0.01mm波动增加到0.78 mm,而内边界层以下过渡区域的空气动力学粗糙度在10-6~0.1 mm之间波动。高度为60 mm和100 mm的10组床面,湍流内边界层空气动力学粗糙度从0.65 mm逐渐增加到30.75 mm,而在此层以上或以下空气动力学粗糙度在0.0002~5.22 mm之间波动。6组孔隙粗糙元覆盖床面(NO21~26),随着侧影盖度增加和孔隙度减少,湍流内边界层的空气动力学粗糙度从0.7 mm增加到12.9 mm;内边界层与近壁区-尾涡区的过渡区,其空气动力学粗糙度约在0.003~0.02 mm之间波动;内边界层以上过渡区的空气动力学粗糙度在0.02~2.20 mm之间波动。内边界层风廓线特征反映整个粗糙元与边界层湍流相互作用,据此推测的空气动力学粗糙度能更好地反映粗糙床面的空气动力学性质,而风廓线符合对数律的过渡区域,由于受到单个粗糙元尾涡或者受上风向气流性质的影响,它们的空气动力学粗糙度很难反映整个床面的空气动力学性质。如果忽视粗糙床面风廓线转折特征和湍流边界层垂直差异,而仅从粗糙元顶端以上风廓线来推测空气动力学粗糙度,则可能低估粗糙床面地空气动力学性质。从表3-5可以看到,根据内边界层风速廓线计算的空气动力学粗糙度比Raupach(1980)算法高几倍甚或一个数量级。因而根据对数廓线推测粗糙床面的空气动力学粗糙度时,需要系统分析风廓线转折特征和确定内边界层范围,才可能获得物理意义明确的真正反映整个粗糙床面的空气动力学粗糙度数据。
由于受粗糙元高度、高度与间距比、方向比率、孔隙度和侧影盖度等因素的综合影响,不同粗糙床面的湍流内边界层范围有所不同。本文确定的细高粗糙元和孔隙粗糙元覆盖床面内边界层范围与Lee ＆amp; Soliman(1977)研究相似,而粗矮粗糙元床面的内边界层范围与类似几何形状的粗糙床面的研究基本一致(Raupach, 1980; Raupach, et al., 1996),这预示在确定内边界层范围和推测粗糙床面的空气动力学粗糙度时,不能简单地以粗糙元顶端作为分界点,而应仔细地考虑风廓线转折特征并以此作为确定依据。
前人对内边界层以上或以下的过渡区域气流性质很少讨论,从本文结果来看,大多数细高粗糙元和孔隙粗糙元的内边界层之上或之下都存在过渡区域,反映了单个粗糙元尾涡、上风向气流性质与整个床面粗糙元之间复杂的相互作用过程。前人强调在粗糙元密度较低(λ＆lt;0.1)或粗糙元间距很大情况下(间距大于10~15 H),粗糙元顶端以下相邻粗糙元之间风廓线符合对数律(Wooding, et al., 1973; Arya, et al., 1975; Alfaro ＆amp; Gomes,1995; Marticorena, et al., 1997),则该风廓线对应的空气动力学粗糙度了反映光滑地表对湍流阻力特征。从本文结果来看,在粗糙元密度较大且相邻粗糙元间距较小情况下(见表3-4),湍流内边界层以下过渡区域的风廓线虽然符合对数律,但其对应空气动力学粗糙度并不反映粗糙元之间光滑床面的性质,而反映了内边界层气流与单个粗糙元背后尾涡层气流的相互作用特征。
4)粗糙床面湍流边界层垂直分化与跃移起动的关系
粗糙床面湍流边界层垂直分化也反映在各层湍流切应力的差异。尾涡层湍流切应力随高度而变化,属于非常应力层,此区域切应力难以从风廓线数据来推测。内边界层及过渡层均属于常应力层,可以用摩阻风速来说明平均切应力。
在自由风速为12 m·s-1情况下,细高粗糙元的近壁区-尾涡层与内边界层的过渡层的摩阻风速约在0.16~0.42 m·s-1之间波动,平均值为0.31 m·s-1,该层平均摩阻风速约为内边界层的15%~64%(见表3-5、图3-15)。孔隙粗糙元近壁区-尾涡层与内边界层过渡层的摩阻风速约在0.16~0.21 m·s-1之间波动(见表3-5、图3-15),约是内边界层摩阻风速的10%~20%。该过渡层的摩阻风速随粗糙床面空气动力学增加而波动特点说明该层气流还受单个粗糙元尾涡等因素的影响。
内边界层摩阻风速约在0.50~1.66 m·s-1之间变化,且随着粗糙床面空气动力学粗糙度增加而增加(见图3-15),细高粗糙元、孔隙粗糙元和粗矮粗糙元覆盖床面的湍流内边界层的摩阻风速随空气动力学粗糙度变化趋势基本一致,当Z0＆gt;14 mm摩阻风速增加趋势减弱。内边界层的平均摩阻风速可看作是整个粗糙床面湍流切应力。
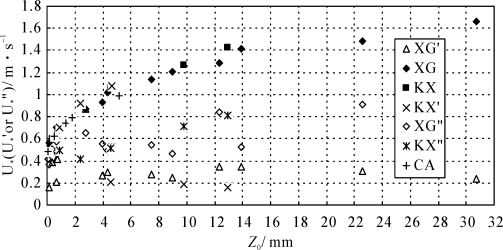
图3-15 粗糙床面湍流边界层摩阻风速(U∗)随床面空气动力学粗糙度(Z0)的变化
XG, XG′, XG″, KX, KX′, KX″含义与图3-14相同。CA为粗矮粗糙元内边界层数据(梅凡民等,2010)。
细高粗糙元覆盖床面的内边界层与外边界层过渡层的摩阻风速约在0.37~0.91 m·s-1之间变化,此层的摩阻风速约为内边界层的36%~87%(见表3-5、图3-15)。孔隙粗糙元内边界层与外边界层过渡层的摩阻风速约在0.42~0.81 m·s-1之间变化,约为内边界层的48%~57%(见表3-5、图3-15)。该过渡层的摩阻风速随床面空气动力学粗糙度增加而波动增加趋势,说明其受上风向气流与粗糙床面空气动力学性质的共同影响。
从近壁区-尾涡区与内边界层过渡层的摩阻风速可以进一步推测的是,近壁区时均雷诺应力可能更小,在此情况下浸没在粗糙床面近壁区的沙粒是如何起动的?
对无粗糙元覆盖的光滑沙质床面而言,湍流边界层可以分为近壁区(黏性底层)和对数区(等雷诺应力层)2个亚层(张兆顺等, 2005),而目前研究沙粒空气动力学起动时,均以对数区的剪切速度(摩阻速度)来表征颗粒起动所受的平均切应力大小,而实际促使颗粒起动的动量可能直接来自黏性底层。早期研究认为黏性底层气流为层流,气流剪切力主要由流体黏性产生,随着对近壁区湍流相干结构的认识,近壁层湍流猝发机制被用来解释沙粒起动。相关研究表明,湍流猝发上抛-下扫循环中的下扫对砾石、沙粒起动起主要作用(Heathershaw ＆amp; Thorne, 1985; Sterk, et al., 1998; Leenders, et al., 2005),这可能说明正是通过下扫过程使得对数层的一部分动量垂直输送到黏性底层而使黏性底层瞬时切应力足以沙粒。最近野外风沙流实验发现(Sterk, et al., 1998; Leenders, et al., 2005),瞬时跃移通量与跃移层以上下扫和注出结构存在明确的对应关系,但瞬时切应力与瞬时跃移通量的相关性很低,这可能由于沙质床面近壁区与对数区(相当于跃移层以上)湍流猝发在强度和相位存在差异而造成的,而沙粒起动可能直接和近壁区的湍流猝发结构相关。因而可以推测的是,借助于湍流猝发对数区的一部分动量被传递到近壁区并使沙粒起动。这暗示了近壁区和对数区湍流猝发存在耦合关系和动量垂直交换机制,而动量垂直交换机制可能是造成近壁区沙粒起动的直接原因。
按照Schlichting的观点(Marshall, 1971),粗糙床面对气流阻力可分解为整个粗糙元和地表对气流阻力之和。相关研究认为(Wooding, et al., 1973; Arya, et al., 1975; Alfaro ＆amp; Gomes, 1995; Marticorena, et al., 1997),在粗糙元密度很低情况下(λ≤0.1)当气流与粗糙元相互作用达到平衡时,粗糙元高度以上和粗糙元高度以下风廓线分别服从对数律,对应的摩阻风速分别代表整个床面湍流切应力、相邻粗糙元之间的光滑地表湍流局部切应力。本文研究表明,内边界层以下过渡层气流的摩阻风速并不能表征粗糙元之间地表对气流阻力或地表从气流所获动量,而近壁区气流切应力可能与粗糙元之间地表所获动量相关,但近壁区平均动量很低。与光滑床面相似,也可以从近壁区湍流猝发角度来理解沙粒起动和粗糙床面动量分配机制,但这可能涉及近壁区湍流上抛运动的诱导与内边界层、过渡层下扫运动等更复杂的耦合机制,通过此耦合机制使一部分内边界层湍流动量依次向下传递到过渡层、尾涡层和近壁层,并使近壁区沙粒起动。
虽然目前研究还不能确定哪些因素如何定量地影响到内边界层动量在近壁区、尾涡区和过渡区分配比例,但从粗糙床面湍流边界层分化特征和湍流猝发角度来探讨粗糙床面内边界层与近壁区瞬时动量传递过程和动量分配关系,可能为研究粗糙床面沙粒起动的力学机制提供了新思路。
综上所述,粗糙床面风廓线具有4个转折段,对应的床面气流分别为近壁区-尾涡区、过渡区、内边界层、内边界层与外边界层的过渡区,其中细高粗糙元和孔隙粗糙元覆盖床面气流垂直分层明显,而粗矮粗糙元等覆盖床面的气流仅有近壁区-尾涡区和内边界层,不存在明显过渡区。
细高粗糙元覆盖床面的内边界层约在0.5H≤Z≤6H之间,而粗矮粗糙元内边界层约在Z≥1~1.5H以上。内边界层风廓线特征反映了粗糙床面对湍流阻力特征,对应的空气动力学粗糙度比其以上或以下的过渡区大几倍甚至一个数量级,比Raupach算法得到的空气动力学粗糙度高几倍到甚或1个数量级。根据对数风廓线来计算空气动力学粗糙度时,以内边界层风廓线推测的床面空气动力学粗糙度能更好地反映粗糙床面的空气动力学性质。
内边界层与近壁区-尾涡区的过渡区风廓线服从对数律,但其空气动力学粗糙度与粗糙元之间光滑地表的空气动力学性质无关,对应的摩阻风速也不能反映光滑地表所受到气流切应力,而近壁区气流切应力虽然直接地反映了粗糙元之间光滑地表所受到气流切应力,但是近壁区气流平均切应力很小,很难直接导致床面沙粒起跳。
这里引出的问题是,气流如何使得沙粒起跳,是壁面附近的气流还是壁面外层气流的冲击?目前研究似乎不能回答此问题。
5) 粗糙副层和惯性副层空气动力学粗糙度随粗糙元高度和密度的变化
正则化的粗糙副层空气动力学粗糙度(Z0r/h)随着粗糙元密度(λ)的增加以对数函数增加。对致密粗糙元而言(CE, 见图3-16),当粗糙元密度从0.02 增加到0.51时,Z0r/h从10-2增加到 10-1,对应的拟合对数函数式为(3-34):
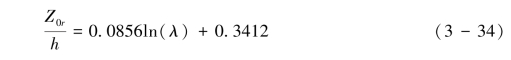
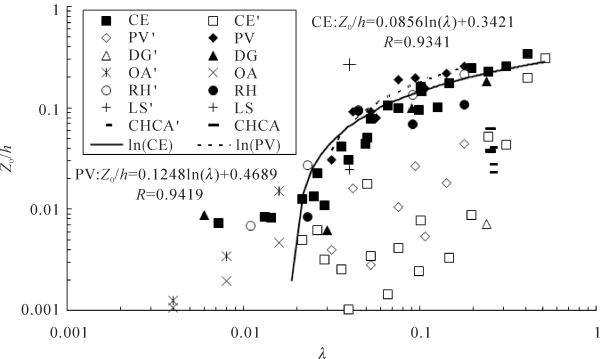
图3-16 正则化空气动力学粗糙度(Z0/h)与粗糙元密度的关系 (λ)
CE为致密粗糙元, PV 孔性粗糙元,DG 为 Dong et al.(2001)数据, OA 为O'Loughlin ＆amp; Annambhotla (1969)数据,RH 为Raupach (1980)数据, LS 为Lee ＆amp; Soliman (1977)数据, CHCA 为Cheng ＆amp; Castro (2002)数据,所有带′为惯性副层数据(梅凡民,2013)。
式(3-34)显示的趋势与前人研究趋势相似,且略高于前人的结果(Loughlin ＆amp; Annambhotla, 1969; Raupach, 1980; Dong, et al., 2001; Cheng ＆amp; Castro, 2002)。作为一个例外,Lee ＆amp; Soliman (1977)的数据显著地超过了著者和以前研究者数据。
孔性粗糙元正则化粗糙副层空气动力学粗糙度也随着粗糙元等效密度增加以对数函数式(3-35)增加:
函数式(3-35)高的相关系数(R=0.94)表明粗糙元几何孔性指数对气流的影响相当于等效粗糙元密度的影响。此正则化空气动力学粗糙度略高于致密粗糙元,可能是由于致密粗糙元围城的丛状孔隙粗糙元促使了粗糙元背后尾涡发展和相互作用并进而提高了床面空气动力学粗糙度。有人发现当几何孔性指数小于30%时,孔性粗糙元空气动力学行为与密实粗糙元相似(Minvielle, et al., 2003)。著者发现当几何孔性指数达到75%时,正则化空气动力学粗糙度也与密实粗糙元有相似的特征,即都可以表示为粗糙元密度或等效密度的对数函数。
就致密和孔性粗糙元惯性副层的空气动力学粗糙度来看(见图3-16中CE′, PV′),当粗糙元密度从10-3增加到10-1时,正则化空气动力学粗糙度Z0i/h是无规则的变化,且比粗糙副层数据低一个数量级。此趋势与前人的研究相似(Dong, et al., 2001)。图3-16显示,Raupach(1980)的结果表明惯性副层正则化空气动力学粗糙度随着粗糙元密度增加而以对数函数增加,且Z0i/h超过Z0r/h 趋势与Loughlin ＆amp; Annambhotla (1969)的数据相似。
粗糙副层和惯性副层空气动力学行为的差异反映了两种不同的情形。第一种情形如的Raupach数据显示那样,惯性副层的正则化空气动力学粗糙度随着粗糙元密度增加而增加,且惯性副层的空气动力学粗糙度高于粗糙副层。第二种情形,如董治宝和著者的结果,粗糙副层正则化空气动力学粗糙度随着粗糙元密度增加而增加,且其数值超过惯性副层的数据。Lee ＆amp; Soliman(1977)和Cheng ＆amp; Castro(2002)的数据都符合第二种情形。
上述两种情形的差异主要与粗糙床面粗糙元高度与边界层厚度比值(h/δ)有关。另外像粗糙元形状、空间分布形式以及粗糙元密度也对粗糙副层和惯性副层的分化产生影响。如表3-6显示,著者和前人研究的最显著的差异在于粗糙元高度与边界层厚度的比值(梅凡民,2013)。Raupach的粗糙床面的h/δ在0.04~0.06之间,其值低于董治宝和著者的数据。较高的h/δ导致了粗糙副层的空气动力学粗糙度能更好地表征粗糙元对气流的阻滞效应。当然,作为一个例外,O'Loughlin ＆amp; Annambhotla(1969) 数据显示在h/δ在0.1情况下,由于粗糙元密度较低,其粗糙副层的空气动力粗糙度特征符合第一种情形。
表3-6 前人和著者研究中采用的粗糙元的形状、空间分布形式、粗糙元密度以及高度与边界层厚度比h/δ等参数的比较(梅凡民,2013)
续表
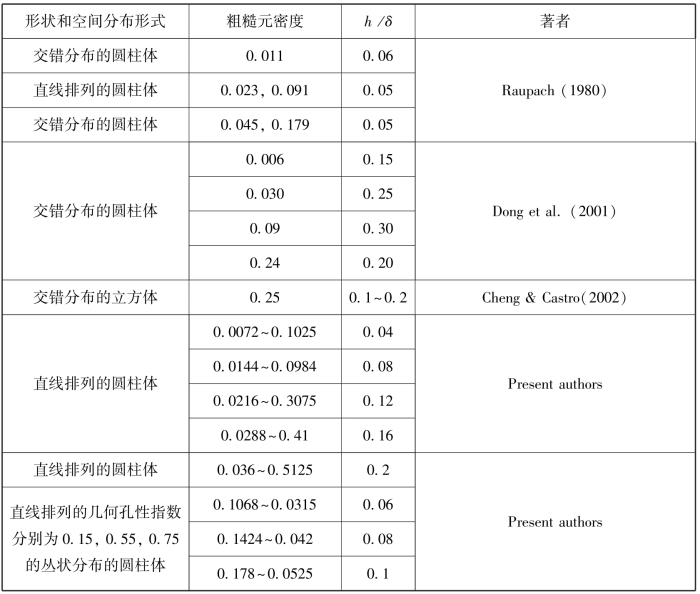
有研究者发现(Cheng ＆amp; Castro, 2002),由于粗糙元的随机分布或者当粗糙元高度超过边界层厚度的4%,则惯性副层会被粗糙副层挤压。著者发现,当粗糙元高度与边界层厚度比超过2%时,粗糙副层得到很好的发育,从而导致惯性副层正则化空气动力学粗糙度随粗糙元密度增加而不规则地变化。
6)粗糙副层空气动力学粗糙度意义及其对跃移起动的影响
粗糙副层正则化空气动力学粗糙度随粗糙元密度增加的趋势表明Z0r代表了整个粗糙元对气流的阻滞效应。以前观点认为,单个粗糙元背后尾涡导致粗糙副层风廓线偏离对数律,因而也就无从谈起惯性副层的空气动力学粗糙度。本文结果表明,在第一种情形下,粗糙副层正则化空气动力学粗糙度随粗糙元密度增加的趋势虽然没有惯性副层的显著,但仍能反映粗糙床面对气流的阻力效应。第二种情形,由于惯性副层的空气动力学性质受到粗糙副层的影响,其正则化空气动力学粗糙度随粗糙元密度增加而呈现不规则的变化,因而在此种情形下,粗糙副层空气动力学粗糙度代表着所有粗糙元对气流的阻滞效应 (见图3-16中的“CE”, “CE′”, “PV”, “PV′”, “DG”, “DG′” )。这些统计结果进一步表明,在第二种情况下,单个粗糙元背后尾涡对粗糙副层风廓线的影响是微不足道的。尾涡的影响范围可能在粗糙副层以下的壁面附近。还有一种可能的情形是,粗糙元密度较大时候单个粗糙元尾涡相互重叠导致了粗糙副层风廓线特征反映了整个粗糙元对气流的阻滞效应。在第二种情形下,和惯性副层相比较,粗糙副层对气流施加了更大的阻滞作用。总之,粗糙副层空气动力学粗糙度反映了粗糙床面对气流的阻力效应。
为了理解粗糙副层空气动力学粗糙度对跃移起动的影响,摩阻风速比值被用来表征空气动力学粗糙度与粗糙床面应力分解和起动摩阻风速的定量关系。该参数被定义为光滑表面起动摩阻风速与粗糙床面起动摩阻风速的比值,其反映了无遮盖区域获得的用于起动沙粒的湍流动量占粗糙床面湍流总动量的比例。粗糙副层和惯性副层的摩阻风速比分别表示如式(3-36)~式(3-37):
其中Rr,Ri分别表示为粗糙副层和惯性副层的摩阻风速比,U∗s, U∗r,U∗i对应着光滑床面的起动摩阻风速、粗糙副层和惯性副层的起动摩阻风速。这里假定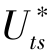
= 0.21 m·s-1。
如图3-17所示,第一种情形下如Raupach数据代表的(见“RH”,“RH′”),粗糙副层和惯性副层的摩阻风速比都随着粗糙元密度增加而降低,且粗糙副层的摩阻风速比低于惯性副层的19%~50%。Gilles et al.(2006) 野外实验表明粗糙副层的摩阻风速比大于惯性副层的数据。Lancaster ＆amp; Baas (1998) 野外实验数据表明粗糙副层摩阻风速比低于惯性副层,这意味着和刚性粗糙元相比较,天然植被由于孔性和柔韧性可吸收了较少的湍流动量。假定大气边界层厚度为200 m,Lancaster ＆amp; Baas (1998)的天然植被数据和Gilles et al.(2006)的刚性植被的粗糙元高度不超过大气边界层厚度的1%,因而惯性副层得以很好地发育。上述两组研究差异主要在于粗糙元形态和空间配置的差异(如方向比率、孔性指数等)。一般而言,在第一种情形下,粗糙元和光滑床面从粗糙副层吸收的动量低于惯性副层。
在第二种情形下,随着粗糙元密度的增加,粗糙副层摩阻风速比从0.7降到0.2而惯性副层摩阻风速比从1.0无规则变化到0.2(见图3-18中的 “CE”, “CE′”, “PV”,“PV′” )。粗糙副层摩阻风速比低于惯性副层的15%~60%,这意味着粗糙元从粗糙副层中吸收了更多的动量,即粗糙副层被粗糙元和床面消耗了更多的动量。有趣的是,著者测定的粗糙副层摩阻风速比与前人惯性副层的数据是一致的(见图3-17)。对此可能合理的解释是,这种一致说明前人数据实际上反映了粗糙副层的摩阻风速比而非惯性副层。事实上,在Marshall(1971)的风洞实验中,粗糙元高度与边界层厚度比(h/δ) 达到 55%,按照Cheng ＆amp; Castro等的观点,这会导致粗糙副层的发育,这意味着此次实验测得数据反映了粗糙副层的空气动力学属性及其对应力分解的影响。同样地,在Musick ＆amp; Trujillo(1996)风洞实验测定的风廓线,其结果反映了粗糙副层的特征,这是因为此次实验中粗糙元高度与边界层厚度比值在5%~16%之间,这也会导致粗糙副层的发育。因而著者有理由相信,前人这些数据实际上反映了粗糙副层的应力分解特征。Lancaster (2004)数据、Marshall(1971)和著者的数据相似,这可能是由于在极端寒冷干燥的沙漠地区砾石的形状和密度在空间分布的不均一性导致了粗糙副层的发育。正如Lancaster(2004)所示,野外沙漠所有实验地点的砾石的底面积与侧面积比值存在着显著地变化(此值在1.8~3.18之间),砾石密度在各个实验点上空间变异系数也很高,其中4个测点的空间变异系数超过0.5。粗糙地表空间异质性可能促进了粗糙副层的发育。具体地说,这次实验风廓线最低测点度高为0.25 m,此位置刚好浸没在粗糙副层内,因而观测的摩阻风速比受粗糙副层的影响更大。Marshall(1971)风洞实验和野外实验间接地证实了在粗糙元高度超过边界层厚度的1%,或者粗糙床面的异质性会导致粗糙副层的摩阻风速比低于惯性副层。
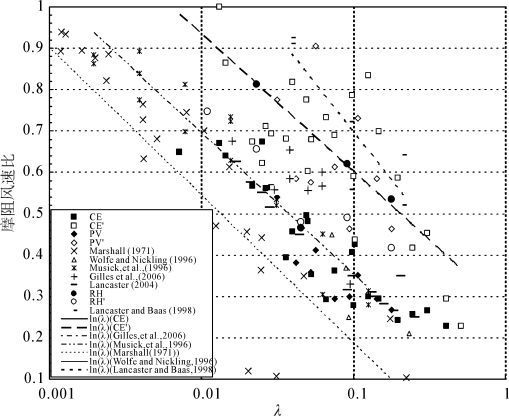
图3-17 前人和著者测定或计算的粗糙副层和惯性副层的摩阻速度比值的比较
图中符号与图3-17相同(梅凡民,2013)。
相应地,粗糙副层起动摩阻风速也能分成2种情形。如图3-18所示,第一种情形如Raupach 数据显示,粗糙副层起动摩阻风速U∗tr在0.2~0.4 m·s-1之间变化,其数值低于惯性副层;第二种情形下,密实粗糙元粗糙副层起动摩阻风速U∗tr在0.4~1.2 m·s-1之间,大于惯性副层的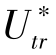
(0.1~0.6 m·s-1之间)。孔性粗糙元其趋势与密实粗糙元相同。由于沙粒更靠近粗糙副层,因而U∗tr代表了用于起动沙粒的动量。也就是说,在一种情况下,U∗ti可能过高地估计了用于起动沙粒真实动量的20%;在第二种情形下,U∗ti过低地估计了用于起动沙粒真实动量的20%~60%。这意味着在两种情况下,Z0r和U∗tr更合适表征空气动力学属性及其对跃移起动影响的参数。
在干旱与半干旱区,一些植物群落高度约在几米之高,其高度常常超过大气边界层中表面层厚度的2%~5%,因而在这些地区大气边界层中粗糙副层容易得到较好的发展。同时较高植物群落叠加在高大沙丘起伏的表面,更进一步促进了粗糙副层的发育。另外,干旱与半干旱地区稀疏植被分布的高度异质性也可能促进粗糙副层的发育。根据邵亚平的综述(2000),在沙丘广布的沙漠地区,沙丘的高度、宽度、长度、间距等特征在小尺度(101~103m)和大尺度(103~105m)上都是高度异质性的,沙丘之间的相对高差在几米到几百米之间,如此大地势差异就像粗糙元一样可能会改变大气边界层的结构,这有利于粗糙副层的发育而限制了惯性副层的发育。同样地,像蒙古高原上广布的,波状起伏的丘陵和山地区域,波峰和波谷相对高差在几百米和千米之差,且波状起伏地形在空间分布上的高度随机性,这些因素可能有利于上述区域粗糙副层的发育。总之,在起伏沙丘区域和波状丘陵地区,粗糙副层得到较好发育的情况下,根据粗糙副层的空气动力学粗糙度来预测起动摩阻风速,可能更符合这些区域的实际情况。也就是说,粗糙副层Z0r和U∗tr是更好表征这些区域风蚀的空气动力学参数。
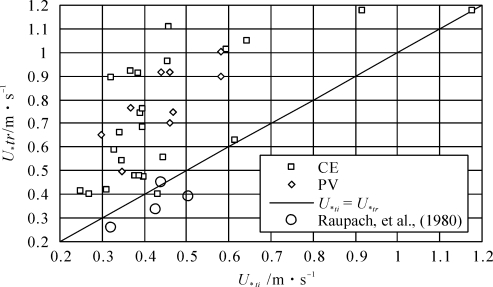
图3-18 计算的粗糙副层和惯性副层的起动摩阻风速(符号与图3-18相同)
3.3.2.2 粗糙元高度以上测点拟合的风廓线及空气动力学粗糙度意义分析
1)粗糙床面风切应力的流向差异和侧向差异
由于粗糙元背后涡旋发育和粗糙元分布方式的影响造成粗糙床面应力分布不均,在来流风速相同情况下摩阻风速和空气动力学粗糙度会有显著的流向差异(图3-19,图3.20),在Uf=10 m·s-1情况下, λ=0.126的NO22床面的摩阻风速从床面前段的0.4 m·s-1逐渐增加到中段的0.5 m·s-1和末段的0.6 m·s-1,在UF=12 m·s-1情况下21号床面的摩阻风速则从0.5 m·s-1依次增加到0.8 m·s-1,说明在下风向末段床面切应力最大,且最大切应力出现在最后2排粗糙元之间。λ=0.066的NO 21床面摩阻风速在流向呈现增加趋势。NO 21 与NO 22相比,随着侧影高度增加湍流应力沿流向增加幅度增大。床面应力流向增加趋势主要与空气动力学粗糙度随流向增加有关,也与粗糙元分布形式有关。本文中所有粗糙元的分布格局为平行式,即各行与流向垂直各列与流向平行而形成风道,在行间形成气流加速区和减速区,而图3-19测定的正好是气流加速区的风廓线。在气流加速区随着流向空气动力学粗糙度增加和气流加速(相对于减速区而言)而导致床面末段切应力最大。在干旱与半干旱区由于稀疏植被空间分布的高度异质性,随着风向不断调整和变化,总会出现这样的风道区,其可能是风蚀剧烈区域,特别是沙漠化草原地区风蚀斑块的出现可能和这样风道区是直接相关的,从这个意义来说,和交错式分布比较,本文粗糙元分布格局可能更有助于理解植被覆盖床面风蚀过程。总体来看粗糙床面末段空气动力学粗糙度和摩阻风速最大,对研究跃移起动而言,此位置观测到的起动能够基本保证整个床面沙粒都有起动。
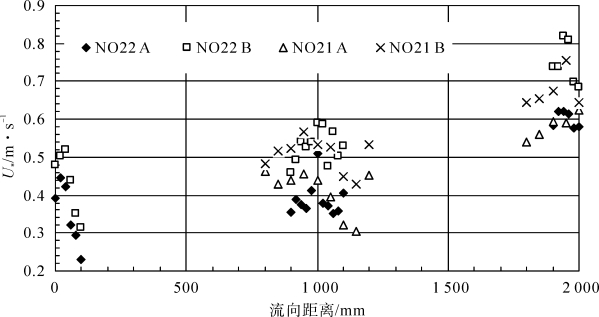
图3-19 摩阻风速流向增加趋势(梅凡民等, 2012)
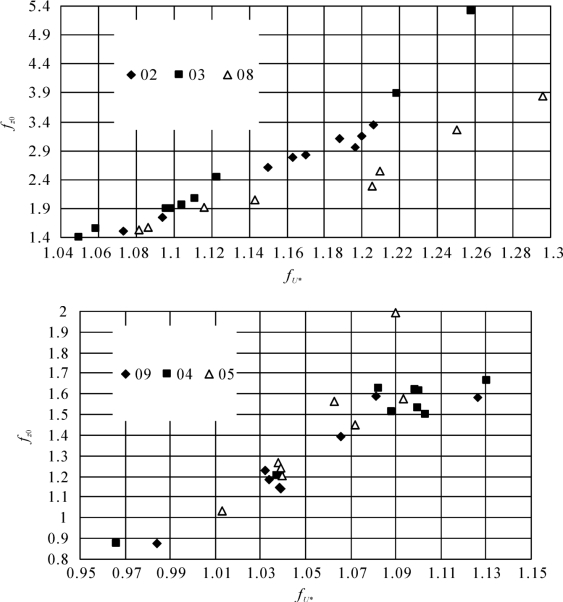
图3-20 U∗和Z0的侧向差异(fU∗,fz0分别为U∗和Z0气流加速区和减速区比值)(梅凡民等, 2012)
由图3-21可以看到粗糙床面气流加速区切应力约为减速区的0.95~1.3倍,而空气动力学粗糙度约为减速区的0.9~5.4倍,总体来看加速区空气动力学粗糙度和摩阻风速高于减速区,且随着侧影盖度的增加气流加速区的空气动力学粗糙度和摩阻风速更大(NO 9, 4, 5的λ在0.04~0.1之间,明显高于NO 2, 3, 8),这可能意味着气流加速区沙粒更易起动(处于涡旋交汇区湍流度高)。
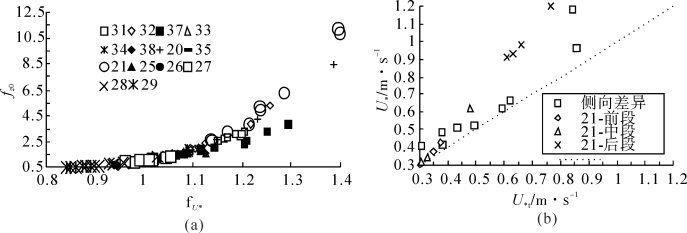
图3-21 (a)高阻力区与低阻力区的摩阻风速和空气动力学粗糙度的比值fU∗和fz0;(b)21号床面的前端、中段和末端的起动摩阻风速(U∗t)和摩阻风速(U∗)以及模拟的粗糙床面低阻力区的起动摩阻风速和摩阻风速(假定前段和高阻力区沙粒处于临界起动状态)(梅凡民等, 2012)
粗糙床面摩阻风速和空气动力学粗糙度流向加速和侧向差异的趋势反映了粗糙床面气流性质的空间异质性本质,其对风沙运动过程有着显著的影响。为了说明粗糙床面空气动力学性质的空间异质性对风沙颗粒起动的影响,利用Marticorena模式来模拟了摩阻风速和空气动力学粗糙度的流向差异和侧向差异对粗糙床面的中段和末段沙粒起动以及低阻力区沙粒起动的影响。根据本文测定的粗糙床面前段、中段和后段的空气动力学粗糙度来计算流向不同位置的起动摩阻风速。假定当粗糙床面的前段的摩阻风速等于起动摩阻风速时(沙粒处于临界起动状态),计算这时床面中段和末段的摩阻风速以说明沙粒起动的流向差异(见图3-21b)。同样地,根据粗糙床面高阻力区和低阻力区的空气动力学粗糙度,计算它们的起动摩阻风速,假定当高阻力区的摩阻风速等于起动摩阻风速时,计算低阻力区的摩阻风速来说明沙粒起动的侧向差异(见图3-21b)。以21号床面为例,当假定该床面的前段风沙颗粒处于临界起动的状态时,中段的摩阻风速在0.23~0.62 m·s-1之间,略高于起动摩阻风速(约在0.25~0.48 m·s-1之间),说明大部分区域的沙粒仍处于临界起动的状态;末段的摩阻风速在0.91~1.25 m·s-1之间,显著地大于起动摩阻风速(在0.61~0.79 m·s-1之间),意味着床面的末段已形成稳定的风沙流。以空气动力学性质侧向差异明显的细高粗糙元(NO 20~21)和丛状分布的粗糙元(NO31~35,37~38)为例,当高阻力区处于临界起动时,低阻力区摩阻风速在0.42~1.19 m·s-1之间,显著地大于起动摩阻风速(起动摩阻风速在0.31~0.81 m·s-1之间),这意味着低阻力区已形成稳定的风沙流。上述的模拟计算表明,粗糙床面的空气动力学异质性对风沙颗粒的起动有显著的影响,在自由风速一定情况下,粗糙床面末端的低阻力区的风沙颗粒最易起动并发展成风沙流,这意味着粗糙床面的风蚀过程具有空间异质性的特征。
本文论述的粗糙床面的低阻力区相当于前人定义的植被覆盖下异质性沙丘地表的街区流(street flow)(即相当于未被植被覆盖的裸露区域)。在干旱与半干旱区由于稀疏植被空间分布的高度异质性,随着风向不断调整和变化,沙漠地表总是会出现低阻力区域,而这些区域正是风蚀剧烈区域。本文研究表明,植被等粗糙元覆盖沙粒地表的风沙输运研究中,更应该关注低阻力区域风蚀过程,而以前研究对此关注还很少,今后需要进一步研究风沙边界层内空气动力学性质的异质性对跃移过程的影响。
由于粗糙床面的低阻力区是最易被风蚀的区域,本文后面仅讨论低阻力区的空气动力学粗糙度。
2)粗糙床面空气动力学粗糙度随摩阻风速的波动
空气动力学粗糙度反映了床面粗糙元对气流的阻滞作用,间接地说明了粗糙元对湍流动量吸收的程度,空气动力学粗糙度随摩阻风速波动说明了在不同湍流应力状况下粗糙元对动量消耗程度的差异。从图3-22可以看到空气动力学粗糙度虽然表现为显著波动,但除密度很高的床面外,U∗约在0.5~0.7 m·s-1之间变化时空气动力学粗糙度达到最大值,然后在小幅度波动中呈现下降趋势。空气动力学粗糙度随摩阻风速波动的特点还与粗糙元形状和密度有关,对细高粗糙元而言(见图3-22a)高度和密度较大床面(如NO21, 22)空气动力学粗糙度随风速波动幅度很大(几个mm级),且不易看到明显下降或上升趋势,随着密度减小Z0波动幅度减小且随U∗增大呈减小趋势。粗矮粗糙元也有类似趋势(见图3-22b)。而对粗矮丛状具有一定孔隙度的粗糙元而言(见图3-20b),Z0随U∗的变化似乎与密度和孔隙度无关。
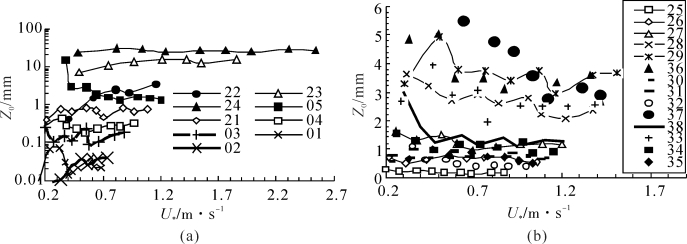
图3-22 空气动力学粗糙度Z0随摩阻风速的波动特征(粗糙床面的编号与表3-2,表3-3同)(梅凡民等, 2012)
大体而言U∗在0.5~0.7 m·s-1之间变化时大多数床面空气动力学粗糙度趋向最大值,而在此范围的摩阻风速与起动摩阻风速接近,这就意味着风速接近颗粒起动阈值时粗糙元耗损的动量最多,此时的粗糙元空气动力学粗糙度实际上最能反映粗糙元空气动力学性质对应力分配和跃移起动的影响,在模拟跃移起动研究时选择此情况下的空气动力学参数可能是最佳的。
对细高粗糙元、粗矮粗糙元和丛状粗糙元覆盖的床面而言,其空气动力学粗糙度均随着自由风速增加具有明显的波动特征,在自由风速大于12 m·s-1时空气动力学粗糙度的波动性减弱而逐渐趋于稳定值。随着粗糙元高度和密度的增加,细高粗糙元空气动力学粗糙度随摩阻风速增加而波动的幅度增大,如1~5号粗糙床面,空气动力学粗糙度在10-2~10-1mm之间波动,而粗糙元高度和密度更高的21~24号床面的空气动力学粗糙度在10-1~101mm之间波动。粗矮粗糙元和丛状粗糙元的空气动力学粗糙度在10-1~100mm之间波动,且在自由风速大于12 m·s-1时逐渐达到稳定。和阻力系数随风速的变化趋势相似,空气动力学粗糙度随着风速先增大而后减小,但具有明显波动性的特征。造成这种波动性的原因可能是风廓线的测定和数据拟合的误差所致。当风速在4~10 m·s-1之间时部分床面的湍流没有得到充分地发育,造成惯性副层的风廓线数据与壁面对数律拟合的数据相关性较低(相关系数低于0.98),对应的空气动力学粗糙度与高风速下获得的数据存在较大差异;同时即使在高风速下拟合的数据具有很好的相关性,但由于空气动力学粗糙度对风廓线拟合误差具有很强的敏感性,也会使该参数具有随机波动的特征,董治宝的研究也表明空气动力学粗糙度是比阻力系数更敏感的空气动力学参数,也随风速明显地波动。
鉴于自由风速超过12 m·s-1空气动力学粗糙度趋于稳定的现象,本文采用自由风速12~20 m·s-1之间对应的空气动力学粗糙度均值来反映粗糙床面对气流平均的阻滞作用。
3)侧影盖度和高度与空气动力学粗糙度的关系
图3-23提到的细高粗糙元指方向比率4＆lt;AR＆lt;20的这类粗糙元,具体指的是NO 1~24,粗矮粗糙元指方向比率AR在0.4~1.25之间的粗糙元,这里具体是NO25~29床面,而丛状粗糙元指以丛状分布的粗糙元,这里指NO 30~38床面,丛状分布和平行分布的细高粗糙元的空气动力学粗糙度约为高度和侧影盖度乘积的1/2(见图3-23),这与Lettau和Marticorena分别提出的空气动力学粗糙度模式接近,有所不同的是,当λ＆gt; 0.1, Z0存在着显著的增加趋势。粗矮粗糙元空气动力学粗糙度与细高粗糙元有所不同,Z0随侧影盖度和高度增加较缓,说明粗糙元方向比率可能对空气动力学粗糙度有明显的影响。本组实验模拟的空气动力学粗糙度模式为(3-38)和式(3-39)(梅凡民等, 2012):
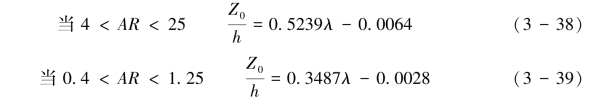
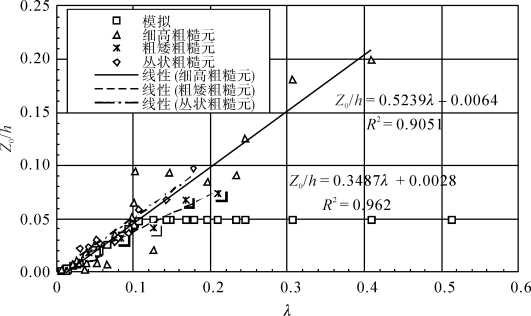
图3-23 侧影盖度(λ)高度(h)与空气动力学粗糙度 (Z0)之间的关系(梅凡民等, 2012)
上述模式表明具有低方向比率的粗糙元,其空气动力学粗糙度比高方向比率粗糙元的空气动力学粗糙度低10%~20%。
目前大多数实验观测的粗糙元排列方式主要是交错式排列,而本实验采用是平行排列方式,存在着气流加速区和减速区,这导致气流加速区空气动力学粗糙度会随着粗糙元侧影盖度增加而增加,直到λ＆gt; 0.4粗糙床面气流由孤立粗糙流演变滑移流,粗糙元阻力系数到稳定,空气动力学粗糙度达到最大。这也说明粗糙元排列方式对气流和空气动力学粗糙度有明显的影响。
4)孔隙度对空气动力学粗糙度的影响
在其他情况相同情况下15%孔隙度引起了空气动力学粗糙度的变化(见图3-24),对h= 50 mm,λ= 0.21的粗糙床面而言,Z0从3.5 mm增加到5 mm,空气动力学粗糙度分别增加了40%;h=40 mm,λ= 0.168粗糙床面的Z0影响不大,h=d=50 mm,λ= 0.21 床面的Z0为1.75 mm,比密实粗糙元空气动力学粗糙度增加了40%左右。当粗糙元孔隙度增加到55%和75%时,空气动力学粗糙度比密实粗糙元大约降低了40%~60%左右,可见孔隙度对空气动力学粗糙度的影响是显著的,这与Minvielle et al.(2008)的研究结果有所不同前人认为植被孔隙度在30%以下才会对空气动力学粗糙度带来显著的影响,从本文结果来看,低孔隙度可增加空气动力学粗糙度,中等和高孔隙度会显著降低空气动力学粗糙度,床面空气动力学粗糙度对粗糙元孔隙度的变化是敏感的,因而在模拟植被空气动力学粗糙度时需要考虑孔隙度的作用。另外可以看到孔隙度对空气动力学粗糙度的影响还与植被高度等因素有关,较高植被的空气动力学粗糙度随孔隙度增加或减小的幅度要明显地大于低矮植被,如h=50 mm粗糙床面Z0的变化幅度明显大于h=30 mm,40 mm的粗糙床面。
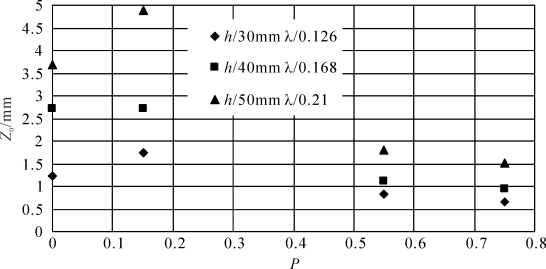
图3-24 孔隙度(P)与空气动力学粗糙度 (Z0)之间的关系(梅凡民等, 2012)
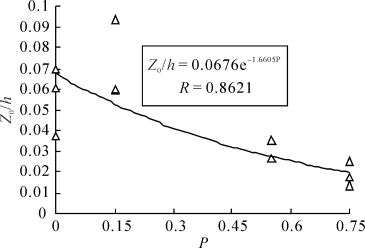
平均地来看,由于丛状粗糙元具有一定的孔隙度和透风效应,减弱了对惯性副层气流的加速效应,导致Z0/h低于细高粗糙元和粗矮粗糙元。然而,Z0/h并不完全是随着孔隙度增加而减小的,在低孔隙度(P=0.15)的情况下,Z0/h大于密实粗糙元,而当P＆gt;0.15时,Z0/h随着孔隙度增加而以负指数函数递减(见图3-25)。孔隙度对气流阻力效应可以从拖曳阻力和肤面阻力的角度来理解。粗糙元对气流的阻力可分为拖曳阻力和肤面阻力两部分(Shao ＆amp; Yang,2009),前者与粗糙元前后的压力损失有关,由于存在透风效应,孔隙粗糙元的拖曳阻力低于密实粗糙元;后者与气流的接触面积有关,而孔隙的存在可能在一定程度上提高气流与粗糙元的接触面积,特别是野外天然植被具有更加复杂的三维表面形态,从而使孔隙粗糙元的肤面阻力高于密实粗糙元,而粗糙元的总阻力效应则取决于拖曳阻力与肤面阻力的共同影响。就本文结果而言,在P≤0.15的情况下, 孔隙粗糙元空气动力学粗糙度高于密实粗糙元,可能是由于拖曳阻力小于密实粗糙元而肤面阻力则明显的大于密实粗糙元且肤面阻力起主导作用的缘故(如表3-3,表3-4中的30号床面与27号床面;33号床面与28号床面以及36号床面与29号床面,孔隙粗糙元的等效密度大于密实粗糙元,见图3-24)。当孔隙度从0.15增加到0.55和0.75后,由于更显著的透风效应和更小的接触面积(更小的等效密度有关),拖曳阻力和肤面阻力均低于密实的粗糙元,因而Z0/h显著地低于密实粗糙元。本文结果与Musick et al.(1996)研究结果相似。Minvielle et al.(2003)认为粗糙元孔隙度P＆gt;0.3,才会对空气动力学粗糙度带来显著的影响。从本文结果来看,当P≤0.15时,空气动力学粗糙度大于密实的粗糙元,而当P＆gt;0.15时,无量纲空气动力学粗糙度随着孔隙度增加而以负指数函数递减(见图3-25)。
图3-25 无量纲空气动力学粗糙度高度Z0/h与粗糙元孔隙度指数(P)的关系(梅凡民等, 2012)
Z0/h与P的相关系数仅为0.86(见图3-25),说明孔隙粗糙元的无量纲空气动力学粗糙度不仅受到孔隙度的影响,还受到粗糙元其他几何参数与孔隙度的交互作用的影响。Z0/h与λeq的相关系数为0.94(见表3-8中的CL),明显高于它和P的相关系数0.86,说明粗糙元的等效密度能更好地表征孔隙度对空气动力学粗糙度的影响。从表3-8可知,丛状粗糙元(孔隙粗糙元)的Z0/h与λeq的线性函数关系与低矮粗糙元的基本一致,这也说明孔隙度对空气动力学粗糙度的影响主要在于粗糙元等效密度(与粗糙元和气流的接触面积有关)的作用。Minvielle等认为只有当P＆lt;0.3情况下,孔隙度对Z0/h的影响相当于λeq对Z0/h的作用,而本文结果显示,在0.15≤P≤0.75情况下,上述结论仍然有效。这就意味着,可以用粗糙元等效密度来代替孔隙度,以建立反映孔隙粗糙元和密实粗糙元空气动力学性质的统一模式。和细高粗糙元与粗矮粗糙元相比较,孔隙粗糙元的无量纲空气动力学粗糙度与有效密度的相关系数较低,这可以解释为Z0/h是在9个水平的有效粗糙度和其他几何参数更复杂交互作用所致。这也意味着在粗糙元几何参数存在着多个水平的交互作用情况下,仅考虑粗糙元密度/有效密度和高度的影响是不够的,还需要同时考虑所有几何参数的交互作用所产生的综合效应。
实际上干旱与半干旱地区天然植被类型各异、冠层形态和结构千差万别,使实际植被冠层孔隙形状、大小、空隙数量等参数复杂多变,本文中植被模型仅是对天然植被孔隙度的近似模拟,可能和实际情况还有很大差距,因而目前实验结果只有相对意义。另外目前对植被孔隙度对空气动力学粗糙度的影响机制了解的还很少,孔隙度对空气动力学粗糙度的影响究竟是通过改变了冠层与气流接触面积而影响空气动力学粗糙度,还是涉及湍流结构作用,这有待于继续深入地研究。
5)粗糙元其他结构参数对空气动力学粗糙度的影响
与细高粗糙元不同,粗矮粗糙元无量纲Z0/h随侧影盖度增加幅度较低,说明了粗糙元方向比率对空气动力学粗糙度的影响(见图3-26)。从图3-26可以看到随着粗糙元方向比率增加,空气动力学粗糙度有增加趋势,如λ=0.04, AR从4增加到20,Z0从0.3 mm增加到1 mm;λ=0.2, AR从1增加到20,Z0从4 mm增加到14 mm;但在观测数据中也出现了随着方向比率增加,空气动力学粗糙度变化不明显甚或出现下降现象。这也在暗示影响粗糙元空气动力学粗糙度的因素不仅仅是高度、侧影盖度、孔隙度和方向比率等结构参数。实际上粗糙元的结构参数都是有联系的,如方向比率变化往往和粗糙元高度和侧影盖度变化是联系在一起的,方向比率对空气动力学粗糙度的影响同时还受到高度和侧影盖度制约。由于高度、侧影盖度、孔隙度和方向比率等结构参数的交互作用而使得AR的变化对空气动力学粗糙度影响变得复杂。
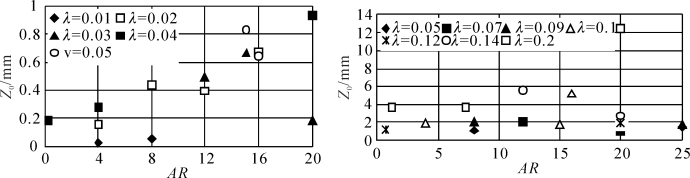
图3-26 植被方向比率(AR)与空气动力学粗糙度 (Z0)之间的关系(梅凡民等, 2012)
研究显示(Musick, et al., 1996),AR的变化对植被与地表的阻力系数之比有显著的影响,在相同的粗糙元密度情况下,AR由0.25变化到0.4,阻力系数比值增加了两倍。Crawley ＆amp; Nickling(2002)的风洞实验研究表明,当AR变化率为50%时阻力系数的变化率为12%,即AR对阻力系数比值的影响作用不大。本文研究表明方向比率对空气动力学粗糙度影响是明显的,与Crawley ＆amp; Nickling(2002) 研究结论相似,AR增加幅度远比粗糙元空气动力学粗糙度增幅大。
一般来说,植被周围形成的涡旋与植被遮盖效应是密切相关的,而涡旋范围受植被高度、AR和孔隙度等结构参数直接相关,因而从这个意义来讲方向比率增大或减小都可能明显影响到植被的遮盖效应,它和植被高度等结构参数具有同等或相近作用。单点空气动力学粗糙度很难反映湍流应力侧向差异,也很难全面反映方向比率变化对风蚀的作用,因而看起来方向比率对空气动力学粗糙度影响不如高度、孔隙度等参数。由于跃移过程是三维的,包括颗粒相和气流相,而目前几乎所有观测和模拟都忽视了这一点,因而AR对植被的遮盖效应和拦截效应的贡献可能被低估了。
空气动力学粗糙度随着高度与间距比增大而增大的趋势是显著的(见图3-27),特别是当0.05＆lt;Sh＆lt;0.4,Z0由10-2mm增加到100mm,增幅达100倍之多;当Sh增大到1.2以后,床面空气动力学粗糙度基本接近到最大值。本文研究结果略高于前人观测结果(Dong, et al., 2001)。上述实验数据差异可能和测定风速廓线的风速系列、粗糙元形状、尺度和侧影盖度等气流和粗糙元结构参数有关。由于空气动力学粗糙度同时还受到侧影盖度和方向比率等因素的影响,在相同高度与间距比情况下,由于侧影盖度或方向比率不同空气动力学粗糙度会有所差异,差异程度取决于这些因素的变化幅度。Lee ＆amp; Soliman(1977)在风洞中研究了侧影盖度和高度与间距比对粗糙元阻力系数的影响。根据λ和Sh把粗糙床面的湍流分为单独粗糙流、尾流相干流和滑移流,在交错排列情况下,当Sh＆lt;0.28时或λ＆lt;0.08为单独粗糙流,0.28＆lt;Sh＆lt;0.44或0.28＆lt;λ＆lt;0.16气流为尾流相干流,本文中粗糙床面气流类型几乎都属于后2种类型,但是没有观测到随着Sh或λ增大空气动力学粗糙度而减小的趋势,实际上反而是增加趋势(阻力系数和空气动力学粗糙度都是反映粗糙元的空气动力学参数,应该有相似趋势)。当然本文中空气动力学粗糙度随Sh增加趋势还可以大体划分为3类型情况,这与Leed ＆amp; Soliman(1977)的分析接近,即Sh＆lt;0.4时Z0随Sh增加最快,对应为单独粗糙流;0.4＆lt;Sh＆lt;1.2之间可能对应着尾流相干流;Sh＆gt;1.2 Z0随Sh增加趋势不明显,湍流涡旋趋于稳定,可能接近滑移流。
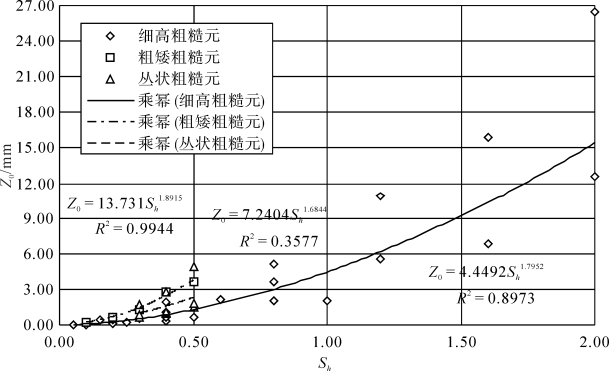
图3-27 植被高度与间距比(Sh)与地表空气动力学粗糙度 (Z0)之间的关系(梅凡民等, 2012)
Z0/h随着粗糙元高度与间距比Sp以幂函数的形式增加(见图3-28),但幂函数的具体形式取决于粗糙元高度与行间距比与其他几何参数的交互作用。粗矮粗糙元的Z0/h与Sp相关性高,是因为随着Sp增大,λ,AR等影响Z0/h的因素也随着增大,这样Z0/h数据离散性降低而与Sp相关性高;细高粗糙元的情形更加复杂,在Sp增加的同时,λ,AR等因素并不是同步地增加的,相同的Sp可能对应着不同的λ和AR,于是Z0/h与Sp的相关性较低。丛状粗糙元的Z0/h与Sp相关性不显著,是因为在Sp相同情况下λeq的显著变化导致Z0/h的显著变化。也就是说,如果在丛状粗糙元的9组数据中,任选一组Sp与λ同步增加的数据,二者必然有较好的相关性。由此可知,Sp与λ/λeq,AR等多因素交互作用的情况不同,相应地Z0/h与Sp幂函数形式亦不同。
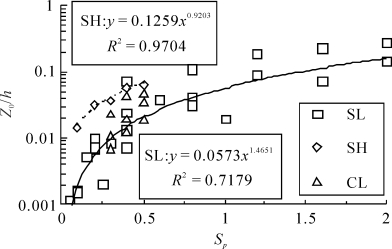
图3-28 Z0/h与粗糙元的高度与行间距比Sp之间的关系(梅凡民等, 2012)
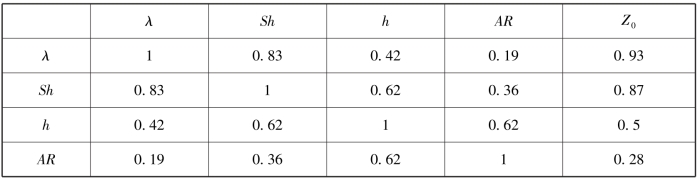
由粗糙元的侧影盖度、高度与间距比和方向比率等结构参数与空气动力学粗糙度相关系数可以看出(见表3-7),侧影盖度对空气动力学粗糙度的影响是第一位的,其次是高度与间距比,方向比率是叠加在前2个因素基础上对空气动力学粗糙度的变化起进一步的“修饰作用”。如前所述,方向比率对气流的影响和风蚀意义还很难完全地从空气动力学粗糙度的变化上得到反映。
表3-7 粗糙元结构参数与空气动力学粗糙度的相关系数(39个样本)(梅凡民等, 2012)
6)粗糙元几何参数的交互作用对空气动力学粗糙度的影响
根据粗糙元几何参数与空气动力学粗糙度的实验数据,可以建立侧影盖度、高度与间距比、方向比率等因素共同作用下无量纲空气动力学粗糙度与侧影盖度的线性关系,见表3-8。
表3-8 粗糙元几何参数交互作用对无量纲空气动力学粗糙度Z0/h的影响(梅凡民等, 2012)
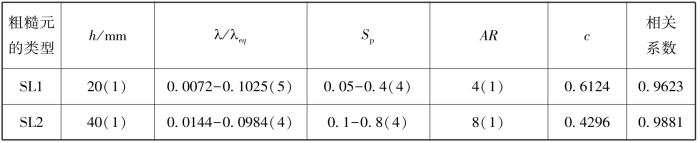
续表
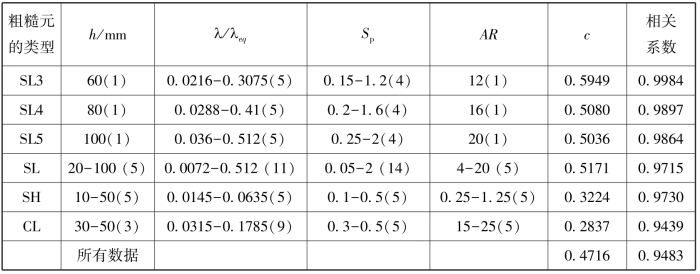
Sp与高度与行间距比,AR-方向比率,拟合方程为Z0/h=cλ,λ为粗糙元密度,λeq为丛状粗糙元的等效密度,c-经验常数,SL-细高粗糙元,SH-粗矮粗糙元,CL-丛状粗糙元,括号内数字表示某个几何参数的处理水平,如(1)表示为1个处理水平。
由表3-8可看到,密实粗糙元无量纲空气动力学粗糙度是粗糙元密度的正比例函数,且比例系数随着粗糙元几何参数的变化而显著地变化(比例系数在0.2837~0.6124之间),该系数的显著变化反映了粗糙元高度、密度和高度与行间距比以及方向比率等多因素交互作用对空气动力学粗糙度的影响。在高度和方向比率一定的情况下,细高粗糙元无量纲空气动力学粗糙度是密度(4~5个不同的密度水平)和高度与行间距比(4个不同的Sp水平下)交互作用下的结果(见表3-4中的SL1-5),对应的比例系数在0.4~0.6之间变化。粗矮粗糙元无量纲空气动力学粗糙度分别是5个不同处理水平粗糙元高度、密度、高度与行间距比和方向比率交互作用的结果,对应的比例系数为0.32。由于交互作用的变量(高度、密度、高度与行间距比和方向比率)多于细高粗糙元,丛状粗糙元无量纲空气动力学粗糙度函数的相关系数较小(0.9439),且比例系数低于细高粗糙元。Letta(1969)认为无量纲空气动力学粗糙度模式的比例系数代表了整个床面阻力系数。本文的比例系数随着粗糙床面几何参数的增加而下降,这可被解释为粗糙元几何参数交互作用的综合效应。
上述实测结果表明,空气动力学粗糙度取决于粗糙元高度、密度/等效密度、高度与间距比等几何参数交互作用的综合效应,这意味着空气动力学粗糙度模式也应反映这一综合效应,而目前的模式主要反映了粗糙元高度和密度的影响。鉴于此,根据本文实测的无量纲空气动力学粗糙度与粗糙元密度、高度与行间距比以及方向比率等参数的交互作用的结果,著者提出一个改进的模式(梅凡民等, 2012):
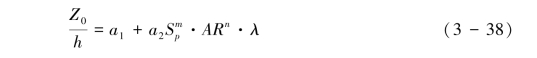
(a1=-0.0028,a2=0.5403, m=0.32, n=-0.07, 相关系数R=0.9732)
确定式(3-38)中Z0/h是Sp的幂函数,是基于本文的实验数据(见图3-29);Z0/h与AR的幂函数关系是根据前人的分析思路(Wooding, et al.,1973)。式(3-38)中经验系数a2,a2,m,n为最小二乘法对所有实测数据拟合所得。
从图3-29可以看到,与Wooding模式和Marticorena模式相比较,式(3-38)显著地减小了风洞实验数据的离散性,实测数据与模拟数据相一致(相关系数达到0.97)。当只考虑Z0/h与粗糙元密度/等效密度的关系,则模拟结果相对于实测数据有明显的离散性(见图3-29中的TD)。Wooding模式考虑了粗糙元高度、密度和方向比率的交互作用对空气动力学粗糙度的影响,但由于所用的Marshall的实验数据中0.2≤AR≤2而本文的0.25≤AR≤25,造成该模式模拟结果与本文实测数据有着显著的差异(见图3-29中的“WD”)。也就是说,当方向比率在更大范围变化的情况下,Wooding模式不能很好地反映粗糙元几何参数交互作用对空气动力学粗糙度的综合影响。当λ＆lt;0.1时,Marticorena模式与本文风洞实验结果有较好的一致性(见图3-29中的“MB”);当λ＆gt;0.1时,Marticorena模式表明空气动力学粗糙度达到了稳定,而实测的Z0/h仍随着粗糙元密度增加而线性增加。造成这种差异主要是由于粗糙元高度对惯性副层及其空气动力学粗糙度的影响。据研究当粗糙元的高度超过边界层厚度的2%(Cheng ＆amp; Castro,2002),粗糙副层的发展会对惯性副层产生挤压效应并影响到惯性副层的空气动力学粗糙度。本文的粗糙元高度约为边界层厚度(本文风洞边界层厚度为500 mm)的2%~20%,因而惯性副层的空气动力学性质必然会受到粗糙副层的影响,而粗糙副层靠近床面对粗糙元密度增加所引起的动量消耗更敏感,于是空气动力学粗糙度具有随着粗糙元密度增加而线性增加的趋势。由此可见,系统地考虑粗糙元密度、高度与间距比和方向比率等因素交互作用的模式(3-38)较好地改进了目前的空气动力学粗糙度模式精度和适用范围。有趣的是,有些学者误认为Wooding的模式强调了高度与间距比的作用(Gilles, et al.,2006),即存在如下的定量关系:
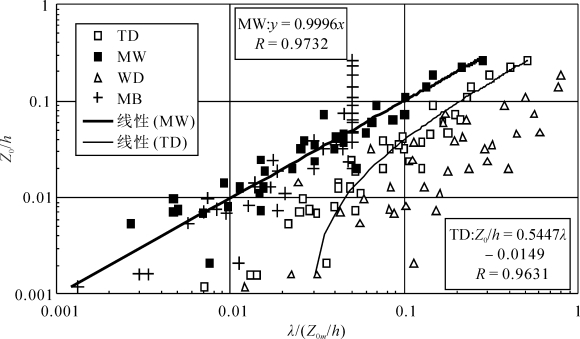
图3-29 TD为本文风洞实测的无量纲空气动力学粗糙度高度(Z0/h)和粗糙元密度(λ)之间的关系
MW是本文模式(3-34)模拟的无量纲空气动力学粗糙度高度(Z0m/h)与实测数据的关系;WD是Wooding模式模拟与本文实测数据的关系;MB是Marticorena模式模拟与实测数据关系(梅凡民等, 2012)。
凑巧的是,本文模式(3-38)看起来与式(3-39)更接近。
3.3.2.3 统一对数区拟合的风廓线及空气动力学粗糙度意义分析
1)确定风廓线统一对数区的方法
当流体流经粗糙元覆盖床面时,边界层被划分为粗糙副层和惯性副层(Raupach,1980)。一般地,粗糙元高度1.5倍以上为惯性副层,其速度廓线服从对数法则,对应的水力学/空气动力学粗糙度可看作整个粗糙元对流体的阻力效应; 惯性副层以下的粗糙副层,由于单个粗糙元尾涡的干扰导致平均流速廓线偏离对数律。因而,一般地,推测粗糙床面的水力学/空气动力学粗糙度均是基于惯性副层的速度廓线。
研究发现粗糙副层风速廓线也符合对数法则且风速梯度明显地高于惯性副层(梅凡民等,2010)。这引申的问题是空气动力学粗糙度的计算究竟是以粗糙副层还是惯性副层为依据。作为对这个问题的探索,笔者曾以粗糙元高度为界拟合风廓线作为床面空气动力学粗糙度(实质是部分粗糙副层和惯性副层叠加平均的结果)(梅凡民等,2012),发现其与粗糙元密度等几何参数有很好的相关性。但这样处理的物理意义及其是否有普适性还需要进一步的讨论。
受流体边界层动量厚度概念的启发(周光坰等, 2001),著者认为,粗糙床面对气流阻力效应的评价应该基于粗糙元对整个边界层风速廓线的影响而不是仅仅考虑惯性副层。若风廓线存在着一个统一对数区(可能包括了以前认为的粗糙副层、惯性副层和近壁-尾涡区),粗糙床面阻力效应就可以表征统一对数区的空气空气动力学粗糙度。直立粗糙元和砾石覆盖床面的风廓线特征的研究结果似乎说明统一对数区存在的可能性(Dong, et al., 2001, 2002; 王晓,张伟民,2014),但是否是真是这样还需要进一步的验证和分析。
研究表明粗糙床面阻力分布具有异质性的特征(Crawley ＆amp; Nickling, 2000),这暗示空气动力学粗糙度不仅受风廓线对数区范围的影响,还与风廓线在床面的观测位置有关,而目前的研究很少关注空气动力学粗糙度的水平变异特征(Cheng ＆amp; Castro,2002),而这对全面理解粗糙床面阻力分解效应显然是不够的。
为了全面理解粗糙床面阻力分解效应,减小空气动力学粗糙度测试的不确定性,本文拟通过测试并分析三类粗糙元覆盖的39组粗糙床面风廓线特征,确定风廓线统一对数区概念和物理意义。在此基础上,揭示风廓线统一对数区内拟合的空气动力粗糙度垂向变化趋势及水平变化趋势,为评估床面阻力效应和预测跃移起动提供合适的空气动力学参数。
在细高粗糙元、粗矮粗糙元和孔隙粗糙元覆盖床面的街流区,风廓线统一对数区下限在0.1~0.3 h之间且此位置随着自由风速和粗糙元几何参数差异而略有差异(见表3-9),这表明街流区风廓线受单个粗糙元下风向尾涡影响不显著。风廓线测定位置2刚好处于周围4个粗糙元的街流中心,受单个尾涡影响是最弱的,可看作是床面对气流阻力最小的位置。
表3-9 街流区和尾涡流区的风廓线统一对数区的范围(自由风速＆gt; 8 m·s-1) (梅凡民等,2018)
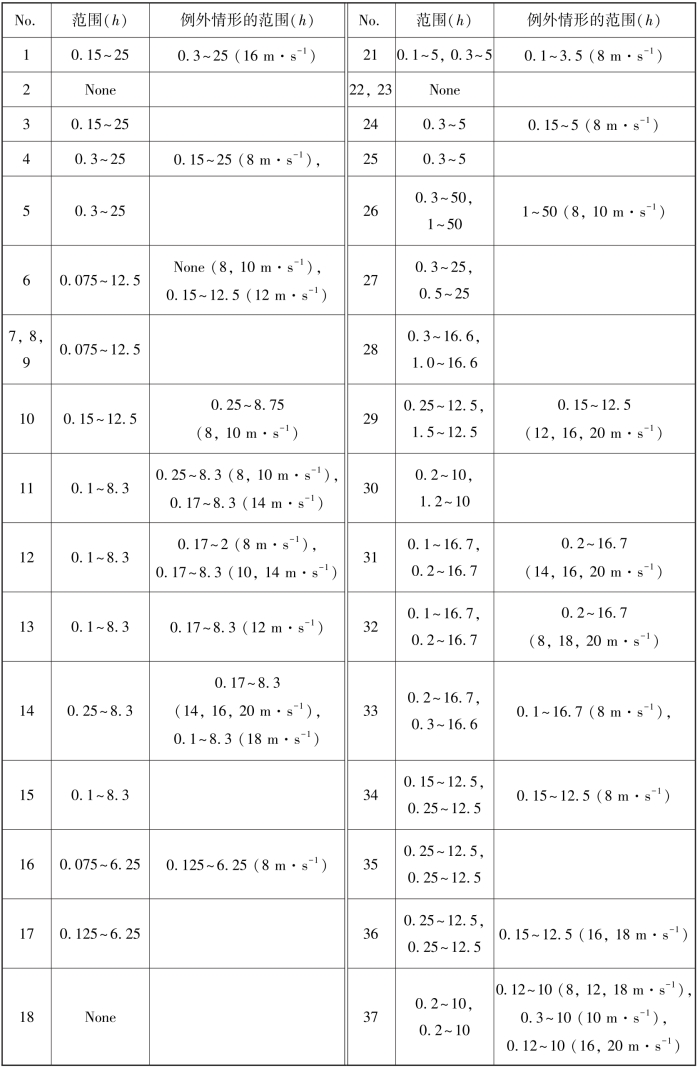
续表
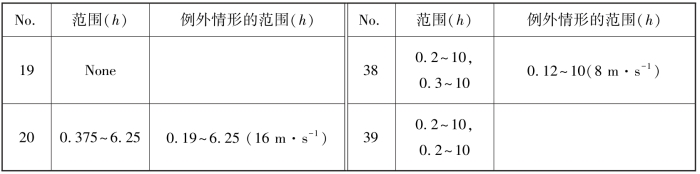
注:正体数字对应街流区,斜体对应尾涡流区,括号里表示对应的自由风速。
除10和21号外,粗糙床面街流区和尾涡流区风廓线的对数区分布上限和实验风洞边界层上限一致(见表3-9),反映了粗糙元整体阻力效应传递到整个边界层。
No.21床面尾涡流区风廓线对数区下限比街流区高0.2 h(见表3-9), 说明尾涡流区的尾涡对风廓线对数律的影响更显著。孔隙粗糙元覆盖床面(表3-3中31~39号床面)也有类似趋势。
除No.27床面外(统一对数区下限为0.3 h),在No.26~30等粗矮粗糙元覆盖床面(方向比率在0.4~1.25)的尾涡流区,风廓线统一对数区下限在1.0~1.5 h之间且随床面差异而略有变化。此下限与Raupach(1980)确定的惯性副层下限基本一致,主要的原因可能是二者床面的粗糙元形状相似:由于同为圆柱体粗糙元且方向比率相近。
应该看到,风廓线测量中还存在未知原因对风速梯度的影响,存在着像2, 18,19,22, 23等床面的风廓线,在其上部或下部某个测点或某几个测点不符合对数律的现象。
总之,细高粗糙元和透风孔隙粗糙元覆盖床面的街流区风廓线统一对数区的下限在0.1~0.3 h之间而尾涡流区与此相似;粗矮粗糙元覆盖床面的街流区风廓线统一对数区的下限0.2~0.3 h之间而尾涡流区则上移到1.0~1.5 h,这意味着方向比率接近1的单个粗糙元背后的尾涡对风廓线统一对数区的下限影响更显著。
前人在风洞中测定直立粗糙元(Dong, et al., 2001)床面和砾石覆盖床面(Dong, et al., 2002)的风廓线转折特点与本文风廓线相似。虽然本文的数据难以和前人数据进行一一比较,但可以推测的是前人的风廓线统一对数区可延伸到粗糙元高度以下(Dong, et al., 2002)。风洞环境下的数值模拟表明砾石覆盖床面的风廓线对数区在0.5~2.5 h之间(王晓,张伟民,2014),与本文风廓线统一对数区的范围有一定的差异。此差异可能与前人模拟的砾石的高度、形状(正三棱锥)和密度等参数与本文粗糙元特征不同有关。
空气动力学粗糙度的空间变异表现在两个方面:一是拟合空气动力学粗糙度随观测高度的垂向变异;二是水平变异,这主要表现在街流区和尾涡流区的差异(见图3-30)。
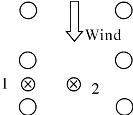
图3-30 粗糙床面尾涡流和街流分布的示意图(○—粗糙元,⊗—测定的风廓线位置)(梅凡民等,2018)
位于相邻两行粗糙元之间受单个粗糙元尾涡的主要影响区(如图3-30的1位置),定义为尾涡流区(wake flow),其中位于该区中点的位置1是尾涡流区受尾涡影响最小的区域;相邻两列粗糙元之间的区域受尾涡流影响很小,定义为街流区(street flow),其中处于前后两排和相邻两列粗糙元中点的位置2可以看作是街流区也是整个粗糙床面阻力最小的。这样,比较位置1和位置2的风廓线特征来表征床面阻力效应的水平变异特征。
2)粗糙床面拟合的Z0随测量高度Z的变化趋势
图3-31表明在No.3, 4, 5 等床面的街流区,风廓线拟合的Z0随着测量高度Z增加呈现先增后减的趋势,约在0.5 h处最大,变化幅度在10-2~100 mm之间且随粗糙元密度和自由风速的变化而变化,此处称为先增后减型。与此趋势不同的是No.1床面, 其拟合的Z0随Z从10-2增加到100mm, 这里称为增加型。在其他细高粗糙元覆盖床面的街流区,No.7~10 (10 m·s-1),No.11~25等床面随测Z变化趋势属于先增后减型(由于篇幅的考虑,这部分数据未在图3-31显示,下同),并在0.3~1.0 h之间Z0最大。与此不同的是,No.10床面Z0随着Z增加而减小(8 m·s-1),此处称为减小型。
在No.21床面尾涡流区,拟合的Z0随Z的变化属于先增后减型。
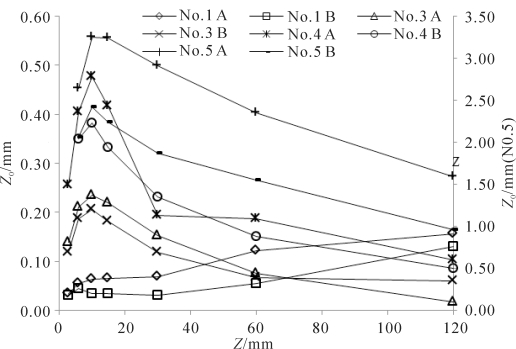
图3-31 No.1, 3, 4, 5等床面的街流区拟合的Z0随测量高度Z变化(A,B分别对应自由风速8,10 m·s-1)(梅凡民等,2018)
在粗矮粗糙元覆盖床面的街流区,No.27~30等床面的Z0随着Z的变化属于先增后减型(见图3-32),且在1.2~2 h之间Z0最大,此特征不同于细高粗糙元覆盖的床面(0.3~1.0 hr之间Z0最大);No.26床面的Z0随着Z的变化属于增加型。
在No.26, 28~30等粗矮粗糙元覆盖床面的尾涡流区,Z0随着Z的变化为减小型,Z0从1 h或2 h处开始减小;No.27床面的尾涡流区Z0呈现先增后减趋势并在0.75 h处Z0最大(见图3-32)。
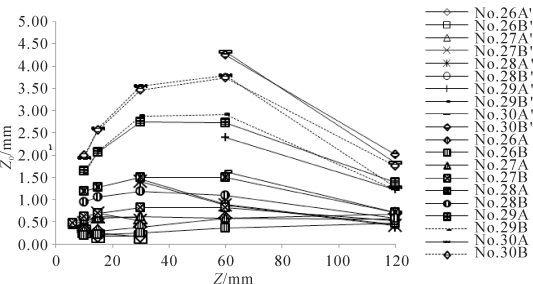
图3-32 No.26~30等床面拟合的空气动力学粗糙度随高度变化(A′与B′系列为尾涡区, A,B分别对应自由风速8, 10 m·s-1)(梅凡民等,2018)
在孔隙粗糙元覆盖床面的街流区,Z0随Z变化趋势也分为三类,先增后减型包括:No.32, 33等床面且在2 h处Z0最大(见图3-33),No.34~38等床面在0.375~1.5 h之间Z0最大,且随着密度和高度增加最大Z0对应的高度低于粗糙元顶部(No.36~38);增加型对应No.31床面;减小型对应No.39床面,Z0从0.2 h处开始减小。
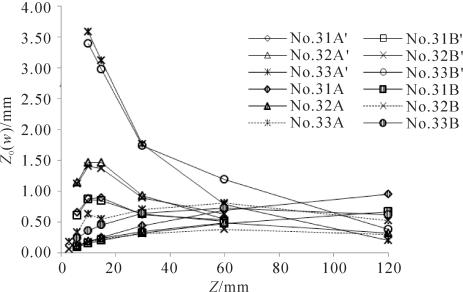
图3-33 No.31~33等床面拟合的空气动力学粗糙度随高度变化(A′与B′系列为尾涡区, A,B分别对应自由风速8, 10 m·s-1)(梅凡民等,2018)
在孔隙粗糙元覆盖床面的尾涡流区,No.31, 32等床面在0.5 h或0.3 h处Z0最大(与自由风速有关),No.34~39等床面在0.6~0.75 h处Z0最大;No.33床面属于减小型,Z0从粗糙元顶部开始减小。
总之,粗糙床面风廓线拟合的Z0随Z的变异趋势可分成三类:先增后减型的概率为71.1%,Z0最大值对应高度与粗糙元类型和流型有关;减小型概率为20.1%,在细高粗糙元、粗矮粗糙元和孔隙粗糙元的街流区或尾涡流区偶有出现;增加型的概率为8.8%,仅出现在稀疏(λ＆lt;0.04)且低矮的(h/δ＆lt;0.06, δ为边界层的厚度)粗糙元覆盖床面的街流区。
本文观测的Z0随Z先增后减的趋势反映了边界层风速梯度的垂向变化。此趋势与前人在风洞观测的砾石覆盖床面风速梯度的垂直变化趋势相似(谭立海等,2012),即在粗糙副层(0.75~1.1 h)之间风速梯度最大而在惯性副层风速梯度逐渐减小。
著者认为,当和粗糙床面相互作用达到稳定状态时,气流将经历床面底层动量急剧消耗-风廓线中部(相当于惯性副层)动量急剧恢复-风廓线上部(相当于惯性副层和外层)平衡-减缓的垂直变化。贴近床面的风廓线底部属于动量急剧消耗区间,其风速梯度较小;风廓线中部某个高度(约在0.5~2 h之间,具体范围因床面特征、自由风速和流型而异)属于动量急剧恢复区间,此对应着传统意义上的粗糙副层及向粗糙元顶部附近的某个高度,其风速梯度、湍流切应力和Z0为整个风廓线最大;风廓线上部气流动量恢复达到平衡状态,风速梯度和湍流切应力不再随高度变化(常应力层),此区间为传统意义上的惯性副层;动量恢复减缓区间为常应力层向外层的过渡,风速梯度和湍流切应力随高度减小。
粗糙床面气流动量垂向消耗-恢复的概念模式可以定性地解释风廓线统一对数区内Z0随Z先增后减的变异特征:统一对数区底部风速梯度较小,动量急剧耗散;统一对数区中部区间风速梯度和湍流切应力最大,气流动量急剧恢复;统一对数区上部是风速梯度、湍流切应力和Z0逐渐减小区间,气流动量缓慢恢复。本文讨论的粗糙床面风廓线统一对数区属于变应力层,其涵盖了传统意义上的近壁-尾涡区、粗糙副层、惯性副层以及外层,其拟合所得的Z0为风廓线统一对数区的垂向平均,反映了粗糙床面对边界层流的阻力效应。对Z0随Z变化的减小型而言,其成因与先增后减相同,只不过由于单个粗糙元尾涡流的影响,在动量急剧消耗区间风廓线偏离了对数律而动量急剧恢复且风速梯度最大的区间刚好位于统一对数区底部所致。至于Z0随Z变化的增加型成因,可以解释为稀疏、矮小粗糙元对气流阻滞效应弱而导致最大风速梯度刚好出现在边界层上部,这与前人在稀疏低矮床面观测到惯性副层风速梯度大于粗糙副层的特征相一致(Raupach,1980)。
传统上以粗糙元高度的1.5倍以上作为惯性副层(Raupach,1980)。本文结果表明惯性副层与粗糙副层以及惯性副层与外层之间的边界可能因床面特征和自由风速而异。由于统一对数区边界的稳定性(见表3-9),在粗糙床面的街流区,风廓线统一对数区的高度稳定在0.1~0.2 h之间,以统一对数区来确定床面的Z0则可以避免传统方法的不确定性。
半经验性的混合长假设是边界层流速廓线对数律的理论依据(周光坰等, 2001),而该假设本身缺乏明确的物理概念。流速廓线对数律是基于常应力层提出的,而本文观测的风廓线统一对数区为变应力层。气流动量耗散-动量恢复的垂向变化模式仅能给予变应力层风廓线对数律的定性的解释,今后工作应该寻求统一对数区常应力层特征的定量的物理解释。
3)粗糙床面街流区和尾涡流区风廓线统一对数区的空气动力学粗糙度
对细高粗糙元覆盖床面而言,尾涡流风廓线统一对数区的Z0比街流区高2~3倍(见图3-34),其具体数值随自由风速略有差异。
平均地看,孔隙粗糙元覆盖床面尾涡流风廓线统一对数区的Z0比街流区高5倍左右(见图3-34),具体数值随床面特征和自由风速略有变化。
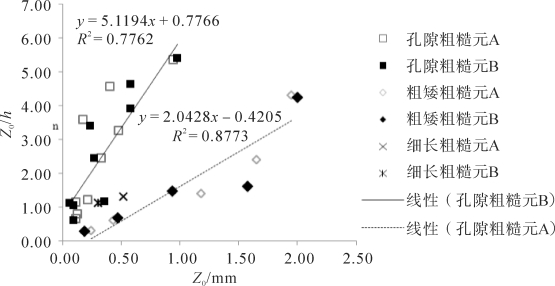
图3-34 尾涡流统一对数区空气动力学粗糙度Z0(W)与街流区Z0的比较(A,B分别对应自由风速8, 10 m·s-1)(梅凡民等,2018)
对粗矮粗糙元覆盖床面而言,其尾涡流风廓线统一对数区的Z0比街流区高2倍左右(见图3-34),具体数值也随自由风速有变化。和前述两类床面不同的是,粗矮粗糙元覆盖床面尾涡流统一对数区仅包括了粗糙副层以上部分的气流特征。
图3-34表明粗糙床面空气动力学阻力效应具有水平异质性,而这会进一步影响到床面沙粒的跃移起动过程及对应的临界湍流切应力。由于推测跃移起动的摩阻风速是基于床面的最小阻力效应,因而以粗糙床面街流区风廓线统一对数区计算的空气动力学粗糙度作为模拟跃移起动参数是最合适的。
4)风廓线统一对数区无量纲空气动力学粗糙度Z0/h随粗糙元密度λ的变化趋势
对细高粗糙元覆盖床面的街流区而言,风廓线统一对数区无量纲空气动力学粗糙度Z0/h随着粗糙元密度λ以幂函数形式增加。粗糙副层及惯性副层与统一对数区Z0/h和λ的关系一致(见图3-35)。统一对数区Z0/h低于粗糙副层和惯性副层,为风廓线垂向平均的结果,即粗糙副层、惯性副层和底层风廓线特征的平均值。
在细高粗糙元中的21号床面的尾流区,风廓线统一对数区Z0/h介于粗糙副层和惯性副层之间(见图3-35)。
在孔隙粗糙元覆盖床面的街流区,风廓线统一对数区Z0/h随λ以幂函数形式增加而粗糙副层和惯性副层Z0/h与λ没有明显的相关关系(见图3-37)。粗糙副层和惯性副层的Z0/h与λ相关性不显著的特征则表明对孔隙粗糙元覆盖床面的街流区而言,用传统惯性副层的Z0/h来表征床面的阻力效应是不合适的。
在孔隙粗糙元覆盖床面的尾涡流区,风廓线统一对数区、粗糙副层以上及惯性副层的Z0/h均随着λ以幂函数增加(见图3-36),统一对数区Z0/h介于粗糙副层和惯性副层之间,其为底层、粗糙副层和惯性副层空气动力学阻力特性的平均。
在粗矮粗糙元覆盖床面的街流区,风廓线统一对数区Z0/h随λ以幂函数形式增加而粗糙副层和惯性副层的Z0/h与λ的相关性低(见图3-37),此特征与孔隙粗糙元覆盖床面的特征相似而与细高粗糙元覆盖床面不同。
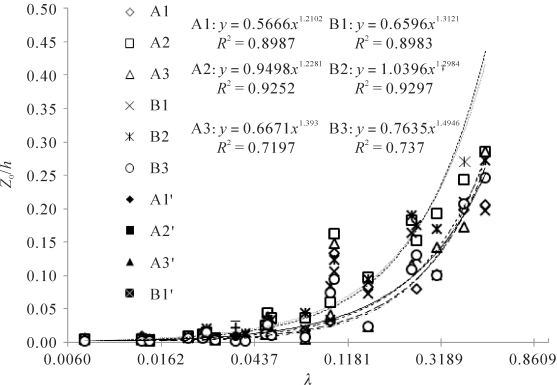
图3-35 细高粗糙元覆盖床面无量纲空气动力学粗糙度(Z0/h)随粗糙元密度(λ)的变化(1-统一对数区、2-粗糙副层以上、3-惯性副层以上;A′与B′系列为尾涡区,A,B分别对应自由风速8, 10 m·s-1)(梅凡民等,2018)
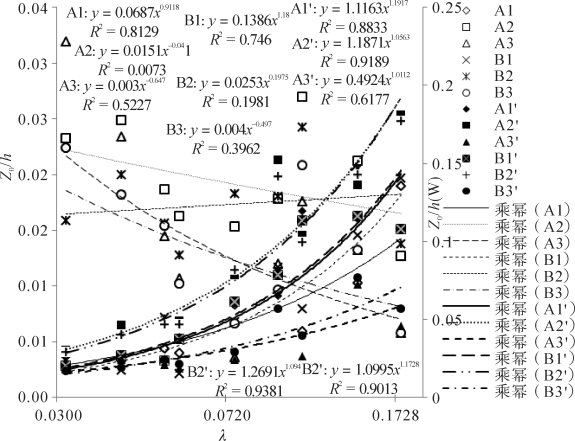
图3-36 孔隙粗糙元覆盖床面无量纲空气动力学粗糙度(Z0/h)随粗糙元密度(λ)的变化(A′与B′系列为尾涡区, A,B分别对应自由风速8, 10 m·s-1)(梅凡民等,2018)
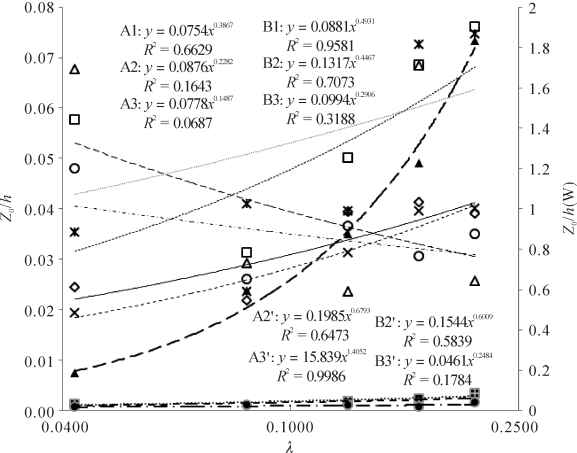
图3-37 粗矮粗糙元覆盖床面无量纲空气动力学粗糙度(Z0/h)随粗糙元密度(λ)变化(A′与B′系列为尾涡区,A,B分别对应自由风速8, 10 m·s-1)(梅凡民等,2018)
在粗矮粗糙元覆盖床面的尾流区,粗糙副层和惯性副层的Z0/h均随λ以幂函数形式增加(见图3-37),但自由风速10 m·s-1情况下,粗糙副层和惯性副层的Z0/h与λ的相关性低,说明空气动力学粗糙度对自由风速的敏感性。
在细高粗糙元、孔隙粗糙元和粗矮粗糙元覆盖床面的街流区,其风廓线统一对数区的Z0/h随λ以幂函数形式增加,但具体数值存在明显差异(见图3-35~图3.37),表明粗糙元形状、类型(密实与孔隙)以及自由风速等因素对床面的空气动力学度有着明显的影响。
在孔隙粗糙元和粗矮粗糙元覆盖床面的尾涡流区,其统一对数区的Z0/h均随λ以幂函数形式增加,而后者统一对数区的Z0/h与λ的相关性略低。
综上所述,和传统的惯性副层空气动力学粗糙度相比较,风廓线统一对数区的空气动力学粗糙度更好地反映了粗糙床面对气流整体阻力效应。
5)有关问题的讨论
最新的空气动力学粗糙度的研究仍是基于边界层为常应力层和风速廓线对数律的认知(高咏晴等, 2014; Sun, et al., 2016; Gilles, et al., 2017),而常应力层和对数律是基于混合长假设。从物理过程来看,混合长假设很难在实际流体中找到真实的物理模型。从这个意义而言,常应力层和风廓线对数律还缺乏清晰、定量的物理解释。
考虑到单个粗糙元背后尾涡流对风廓线的干扰,传统上以惯性副层作为常应力层的范围,而惯性副层受风速、粗糙元形状、密度以及粗糙床面的流型(如街流与尾涡流)等因素的影响,其范围是变动的而非固定的。另外,粗糙床面的边界层上部还存在着惯性副层和外层的过渡区域。本文数据揭示了空气动力学粗糙度的垂向变化和水平变异趋势,既说明了惯性副层范围的不确定性,也说明了空气动力学粗糙度对上述相关影响因素的敏感性。本文提出的风廓线统一对数区的空气动力学粗糙度避免了上述测试结果的不确定性。
本文风廓线数据表明单个粗糙元尾涡流对风廓线的影响仅出现在粗矮粗糙元覆盖床面的尾涡流区,粗糙元顶部以下的区间的风速廓线偏离对数律。而在其他粗糙床面的街流区和尾涡流区,风廓线统一对数区均向下延伸到单个粗糙元内部。前人相关数据虽然不能用来一一对比,但这些数据所反映的趋势也暗示风廓线对数区可延伸到粗糙元高度以下。但目前不清楚的是湍流变应力层内风廓线符合对数律的机理,此问题和湍流常应力层的混合长假设一样,都是未解之谜。
需要说明的是,本文中判断风廓线是否符合对数律是基于对数函数拟合的R2＆gt;0.9600的条件,而此标准的设置带有经验性。图3-38(a)表明当拟合函数对风廓线对数律的分布区间下延到床面附近时,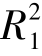
对应的概率为25%,若以R2＆gt;0.97为对数律分布区间的依据,则75%的风廓线对数律的分布区间还能下延至床面附近。图3-38(b)表明当拟合区间从最低点仅上移一个观测点(几个毫米到几十毫米)则
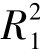的概率降至6.9%而 R2＆gt;0.98的概率则提高至61%。也就是说,虽然拟合风廓线对数律的标准带有经验性,但从统计意义来看,即使再提高相关系数的标准,仍不能改变大多数粗糙床面的风廓线对数律分布区间会下延至床面附近的事实。因而,从统计意义看,粗糙床面风廓线统一对数区是客观存在的,尽管和传统的边界层常应力层的假定不一致。
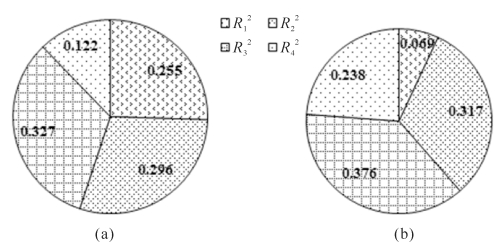
图3-38 风廓线统一对数区拟合的相关系数平方的概率分布((a)为延伸到底层,(b)为最靠近底层点的上部观测点,0.96≤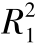
＆lt;0.97, 0.97≤
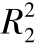＆lt;0.98, 0.98≤
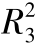＆lt;0.99, 0.99≤
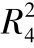)(梅凡民等,2018)
风廓线统一对数区涵盖了风速梯度不同的底层、粗糙副层、惯性副层以及惯性副层和外层的过渡区域,其反映了边界层属于变应力层的特征,其对应的空气动力学粗糙度为床面对边界层阻力效应的均值。风廓线统一对数区无量纲空气动力学粗糙度与粗糙元密度明显的相关性,进一步表明风廓线统一对数区空气动力学粗糙度反映了粗糙床面的整体阻力效应。
本文结果是基于实验观测及数据统计基础上的半定量经验性总结。未来工作需要结合数值模拟工作进一步厘定风廓线统一对数区的物理意义,以阐明其普适性。
6)小结
为了进一步理解粗糙床面阻力效应,减小空气动力学粗糙度测试中的不确定性,依据风沙风洞测试的3类粗糙元(细高粗糙元、孔隙粗糙元和粗矮粗糙元)覆盖的39个粗糙床面在不同自由风速下的风廓线数据,本文提出了风廓线统一对数区的概念并取得以下结论:
除粗矮粗糙元覆盖床面的尾涡流区外(粗糙元高度以上至边界层顶部),风廓线统一对数区从0.1~0.3 h之间延伸到边界层顶部,涵盖了边界层流底部、粗糙副层、惯性副层以及惯性副层和外层过渡区间,其具体范围因床面几何特征和自由风速等因素的变化而略有差异。
粗糙床面风廓线拟合的空气动力学粗糙度垂向变化趋势分为三类:70%的粗糙床面属于先增后减型;21%粗糙床面属于减小型;9%粗糙床面属于增加型。空气动力学粗糙度变化幅度在10-2~100 mm之间,这既反映了空气动力学粗糙度对测量高度的垂向变异,也表明了以风廓线统一对数区空气动力学粗糙度来表征床面阻力效应的可以避免空气动力学粗糙度计算的不确定性。风廓线统一对数区空气动力学粗糙度是变应力层内粗糙床面对气流阻力效应的垂向平均。
风廓线统一对数区无量纲空气动力学粗糙度随粗糙元密度以幂函数形式增加,进一步表明该指标更好地反映了粗糙床面对气流的阻力效应。
平均地,尾涡流区统一对数区空气动力学粗糙度约为街流区的1~5倍(具体数值随粗糙元形状、密度和自由风速等因素的变化而变化),既反映了空气动力学粗糙度的水平变异特征,也表明街流区风廓线统一对数区空气动力学粗糙度是预测跃移起动阈值的更好参数。