4.2 边界层湍流与风沙跃移过程分析
在湍流的视角下如何来理解跃移通量和风况的关系是风沙科学的基本问题。如前所述,半经验跃移通量模式都是假定风场是稳定的,而这个假定在野外是不成立的。从边界层理论来看风蚀过程的气流都是湍流(e.g.Bagnold, 1941),这包括室内风洞的气流也是不稳定的湍流。当然风洞模拟的大气边界层湍流和野外大气边界层湍流在时间和空间尺度上还有很大的差别(胡非,1995;张兆顺等, 2005)。前者利用风洞的蜂窝器等部件把气流中大涡击碎以维持风向的稳定。
图4-1~图4-4显示了毛乌素沙地同步观测的跃移强度(以saltiphone 记录的颗粒数为指标)随摩阻风速(摩阻风速由风廓线数据计算,并考虑了大气稳定度的影响)的变化趋势。结果表明,在1 min时间分辨率下,跃移强度随摩阻风速的变化呈现了随机特征或混沌状况(Baas, 2008),二者缺乏稳定的函数关系,时而一致时而不一致,其对应关系难以捕捉。前人野外观测发现在5 Hz时间分辨率下的跃移强度与摩阻风速呈现更加明显的混沌状况(Baas, 2008)。
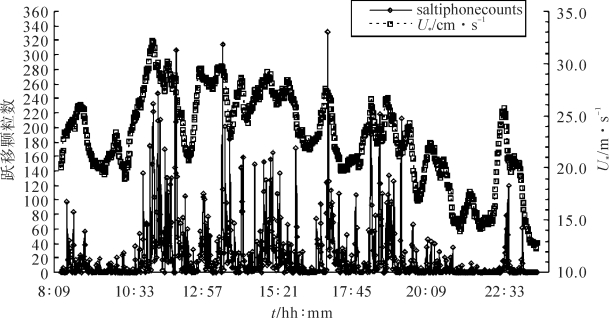
图4-1 2002年4月6日空气动力学粗糙度摩阻风速及输沙率的瞬时变化(梅凡民,2013)
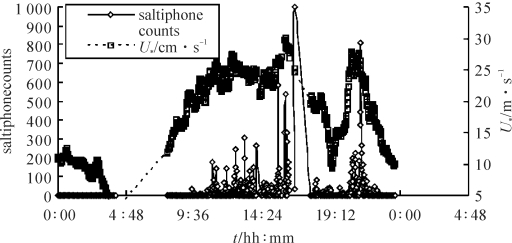
图4-2 2002年4月7日空气动力学粗糙度摩阻风速及输沙率的瞬时变化(梅凡民,2013)
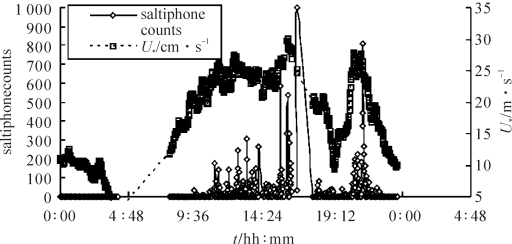
图4-3 2002年4月8日空气动力学粗糙度摩阻风速及输沙率的瞬时变化(梅凡民,2013)
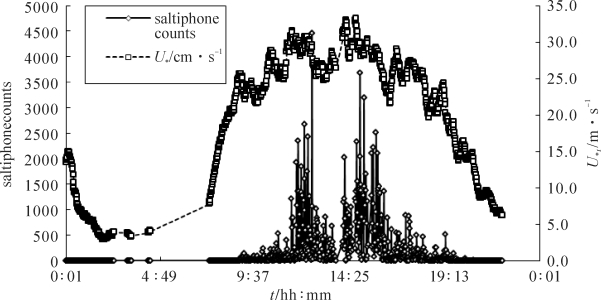
图4-4 2002年4月16日摩阻风速及输沙率的瞬时变化(梅凡民,2013)
表4-2表明无论是统计起动摩阻风速以上的数据,还是统计全部的摩阻风速与跃移强度的关系,跃移强度与摩阻风速在统计上是不相关的,这意味着1min时间分辨率下,跃移输送与摩阻风速的关系是混沌的。
表4-2 瞬时空气动力学粗糙度、摩阻风速和瞬时输沙率的相关系数(梅凡民,2013)
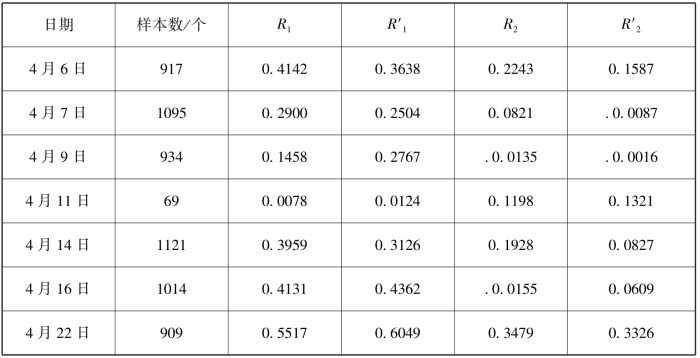
注:R1,R2分别为瞬时摩阻风速、空气动力学粗糙度与瞬时输沙率的相关系数(所有数据);R1′,R2′分别为瞬时摩阻风速、粗糙度与瞬时输沙率的相关系数(仅为输沙率大于零的数据)。
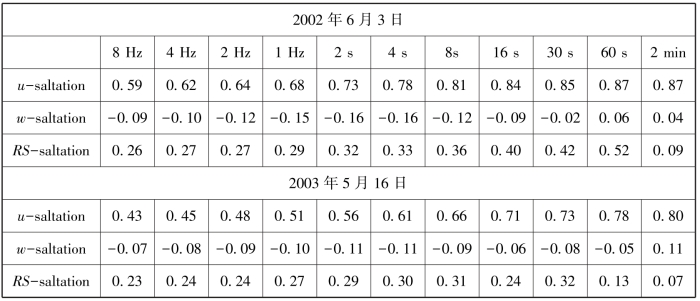
表4-3显示在高时间分辨率下跃移强度与2 m高度风速有较好的相关性(Leenders,et al., 2005),在1~2 min的时间分辨率下二者具有更高的相关系数。然而,跃移通量与垂直风速、运动剪切应力几乎没有相关性。前人的研究结果与本书著者的结果有一致性。有趣的是,Leenders et al (2005)数据在2 min的分辨率下,跃移通量与运动剪切应力的相关系数比1 min还低,其原因不明。
表4-3 跃移强度与2 m高度的水平风速u、垂直风速w及运动剪切应力-u′v′(RS)的相关系数(数据来自Leenders et al (2005)
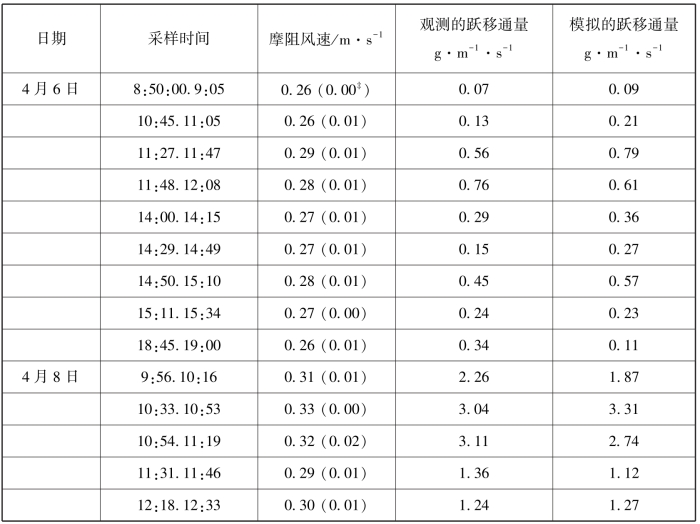
为了进一步理解跃移强度和摩阻风速的关系,这里对毛乌素沙地风蚀数据是进行长时间的平均,得到10~20 min 内跃移通量和摩阻风速的关系(见表4-4)。表4-4显示了跃移通量随摩阻风速的增加而有规律的增加,且二者不再呈现混沌关系。图4-5表明对松散的沙质土壤而言,跃移通量是摩阻风速3次方的函数,这与Bagnold的跃移通量模式和Marticorena & Bergametti (1995)的跃移通量模式基本一致。对有结皮的沙质土壤和壤质土壤而言,跃移通量随摩阻风速的变化会偏离这一趋势。
表4-4 风蚀观测期15~20 min内观测和模拟的跃移通量的比较(梅凡民等,2006)
续表(https://www.daowen.com)
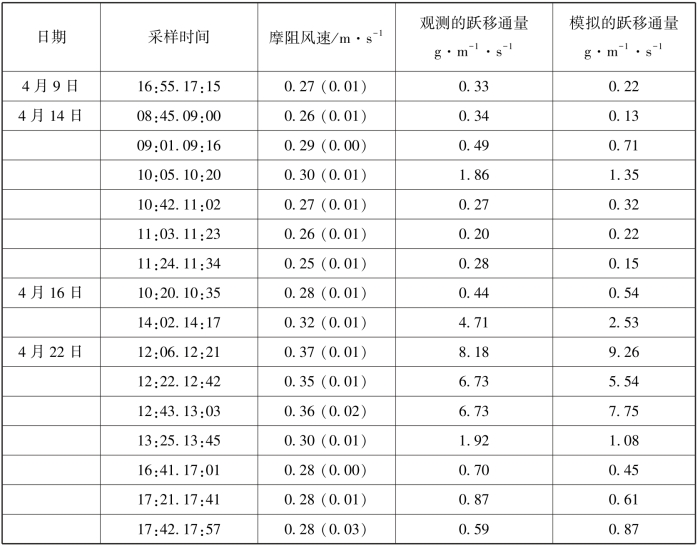
注:括号内数字为平均摩阻风速的标准偏差。
上述的研究案例表明跃移通量与摩阻风速的关系在很大程度上取决于观测及统计的时间分辨率(见表4-5),较长时间分辨率下,二者有明确的函数关系。
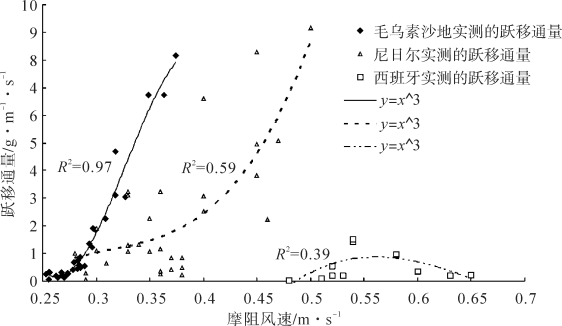
图4-5 不同类型表土风蚀过程中跃移通量定量与摩阻风速关系的比较(毛乌素沙地、尼日尔和西班牙野外实验土壤分别为松散沙质土,有结皮的沙质土和有结皮的壤质土(Gomes, et al, 2003a, b))(Mei, et al., 2006)(梅凡民等,2006)
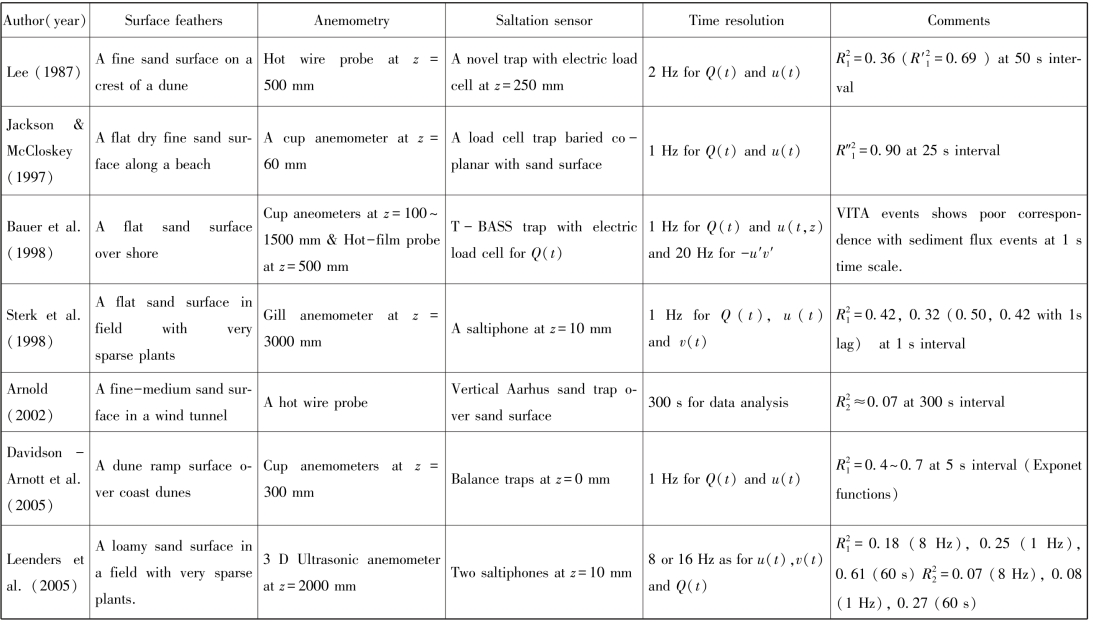
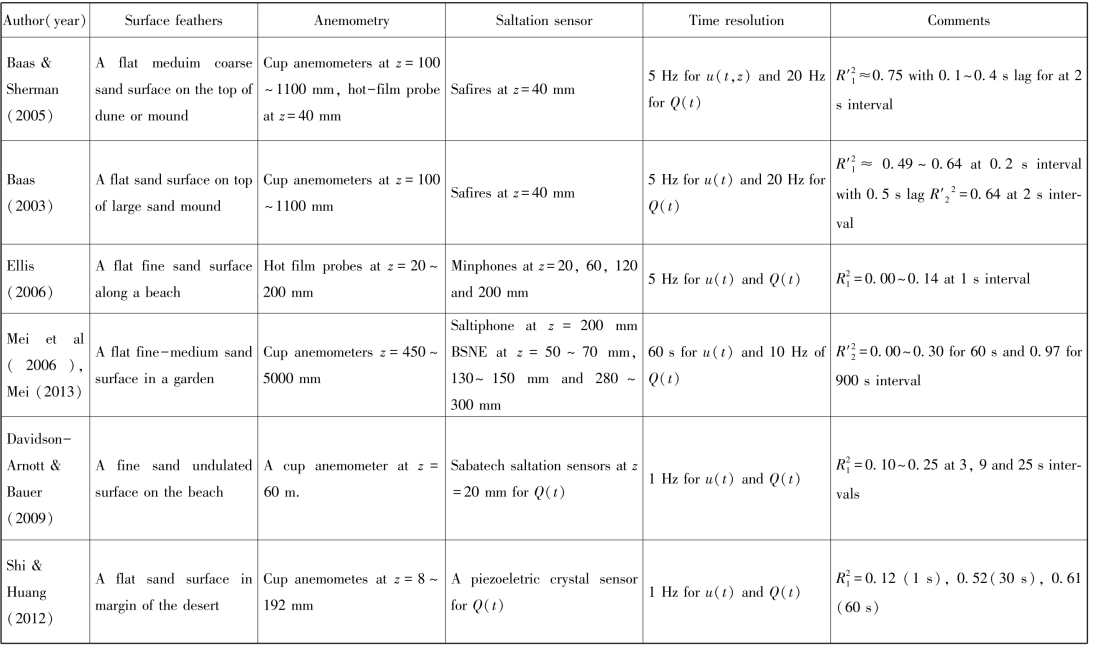
表4-5 前人关于跃移强度Q(t)与边界层湍流参数的关系汇总
续表
续表

表4-6 前人观测的跃移通量对风脉动的响应时间(滞后时间)

续表
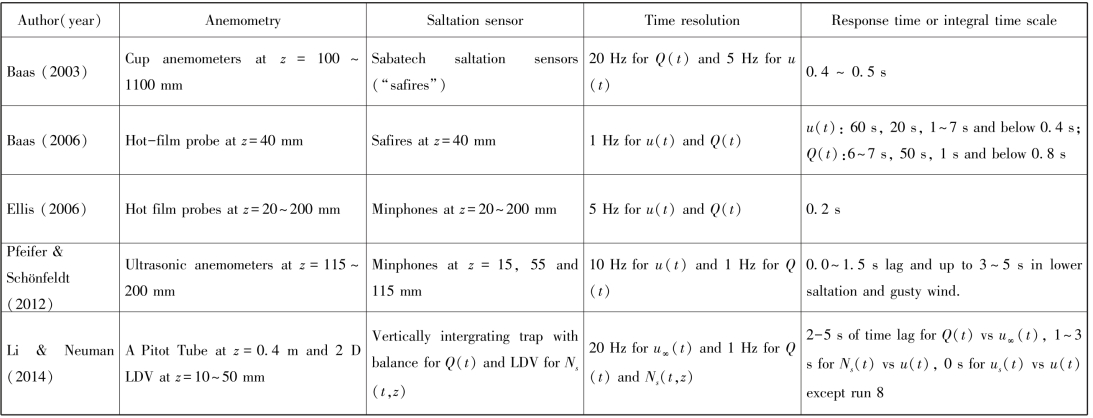
表4-5表明跃移通量和风速之间有较好的一致性,约在1 min时间分辨率下相关系数在0.6以上。不同的观测数据表明跃移通量与风速的关系分别符合线性关系、二次方关系和3次方关系。在更长时尺度上跃移通量与摩阻风速才有显著的相关关系,如统计时间在10 min以上。考虑跃移对湍流响应时间即跃移滞后性后(见表4-6),对跃移通量与风速关系再分析发现在2 s时间分辨率下,二者存在明显的相关性(Baas, 2003),这意味着跃移颗粒群对湍流变化响应的滞后性是影响跃移通量和风速函数关系的重要因素。前人用小波分析的方法分离了不同尺度的湍流结构对跃移输送的影响(Baas, 2006),结果表明存在着4个时间尺度的湍流输送,分别是60 s, 20 s, 1~7 s 和<0.4 s;跃移输送的时间尺度分别为6~7 s, 50 s, 1 s 及<0.8 s。其中1 s反映了风沙颗粒群输送的惯性,1~7 s为边界层上部湍流强迫之下跃移颗粒群对湍流响应的时间尺度,直至在更长时间尺度内形成具有时间和空间异质性的沙流(Aeolian streamers),这意味跃移强度和大尺度流向涡的动量输送有较好的相关性。
从流体力学角度来看,摩阻风速是时均的湍流切应力,其是基于长时间尺度而非短时间尺度的统计,因而在高时间分辨率情境下分析跃移通量与运动剪切应力的关系不符合流体力学的基本假定。湍流结构与跃移强度的研究表明(e.g.Leenders, et al., 2005;Chapman, et al., 2013; Martin, et al., 2013),和水平动量输送的下扫事件/结构、注出事件/结构才对应着显著的跃移输送,而湍流动量输送强度更大的上抛事件/结构对跃移输送的贡献有限, 因而有研究者强调跃移输送过程中湍流水平动量输送起主导作用(Leenders, et al., 2005),半经验模式考虑跃移通量与水平风速的关系是符合微观机理的。
著作认为,沙粒轨迹形成的时间尺度约在10-2~10-1 s之间,近床面附近沙粒轨迹形成时间10-2 s,假定600个沙粒min-1被气流输送,则10 min约有6000颗粒被输送到某个断面。从跃移通量的定义来看,其是长时间尺度跃移输送强度的积分,因而短时间尺度讨论跃移通量缺乏物理意义(短时间尺度属于单个颗粒的输送,它是任意输送断面上不同轨迹沙粒的接力过程,每个沙粒与气流作用时间,吸收气流的动量是千差万别的。从这个意义上说,短时间尺度的输送过程是跃移沙粒的接力过程)。基于跃移沙粒具有相同的运动轨迹假定的半经验模式之所以能在长时间尺度上预测跃移通量(e.g.Bagnold, 1941;Sørensen, 2004),其原因在于长时间尺度下大量沙粒群的轨迹趋向统计平均值。
野外风沙流观测(Baas & Sherman, 2005)表明,风沙流具有时间和空间异质性格局,沙流呈现0.2 m 长、1 m宽的尺度,且此尺度与平均风速无明显关系。以往用单点的跃移通量来描述风沙输送强度的方法显然与实际风蚀过程还存在很大的差距。基于大涡模拟驱动的跃移输送计算能够再现沙流的间歇性、空间异质性及沙流浓度随风速在二维尺度上的演化趋势(Dupont, et al., 2013),是理解风沙跃移的新方法。
对半经验模式和数值模式的验证而言,准确地测定风场和跃移输送强度也是重要的问题。从前人的野外观测来看,风场和跃移输送的观测所采用设备和方法是多样的(见表4-5和表4-6),未来的观测研究需要考虑如何提高测量的精度、改进数据的统计分析方法以及克服样地土壤性质的异质性等问题。例如,风速脉动的计算是否应考虑在只对同一风向的风速进行统计而非对观测时段不同风向的风速数据进行统计,即把不同风向的风速进行统计平均是不符合流体力学要求的。
综上所述,野外风蚀研究表明,跃移受土壤性质如粒径、水分和边界层湍流的控制具有显著的间歇性特征,风沙流具有随湍流结构演化的空间异质性格局,单一跃移通量无法精细地反映风沙流的时空特性,这一发现对传统的风沙跃移观测和模拟带来了新的思考,也为风沙跃移研究提出了新课题。
