3.5.3 结果与分析
3.5.3.1 粗糙元方向比率及空气动力学粗糙度对起动摩阻风速的影响
当Z0从0.02 mm增加到26.5 mm时,U∗t约从0.30 m·s-1以对数函数形式增加到1.45 m·s-1(见图3-41),但U∗t明显的分散性意味着床面的某些结构参数可能对其有着重要的影响。鉴于粗糙元密度、高度对气流的阻滞效应可以通过Z0来表征(Dong, et al.,2002),而粗糙元间距与起动摩阻风速成负相关关系,则意味着方向比率可能是造成摩阻风速数据分散性的主要原因。
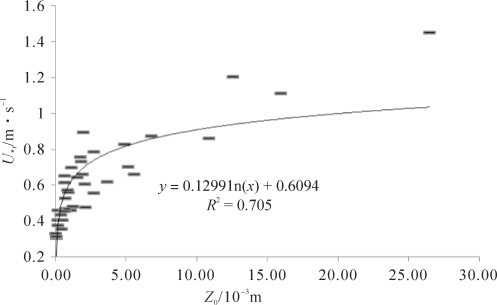
图3-41 风洞实验测量的粗糙床面空气动力学粗糙度Z0和起动摩阻风速U∗
t(梅凡民等, 2020)
图3-42a和图3-42b表明在相近的或相同的AR情况下,U∗t与Z0具有更高的相关系数,则意味着方向比率对起动摩阻风速有重要的影响。图3-42a表明当AR从0.25增加到8时,U∗t均随着Z0以对数函数式(3-48)增加,且经验系数a,b因AR的不同而有轻微的变化。
当AR从12增加到25时,U∗t随着Z0以对数函数(3.48)增加,且对应的经验系数a,b则随着方向比率具有明显的线性增加趋势(图3-42b)。
本文用丛状分布的粗糙元来模拟孔隙粗糙元对U∗t的影响,当孔隙粗糙元对应的Z0与密实粗糙元相近,且在AR相近的情况下,丛状分布的孔隙粗糙元(AR=15,20, 25)与密实粗糙元(AR=16,20)分别服从同一对数函数(图3-42b),这表明孔隙率对跃移起动的影响可归结为Z0的影响。
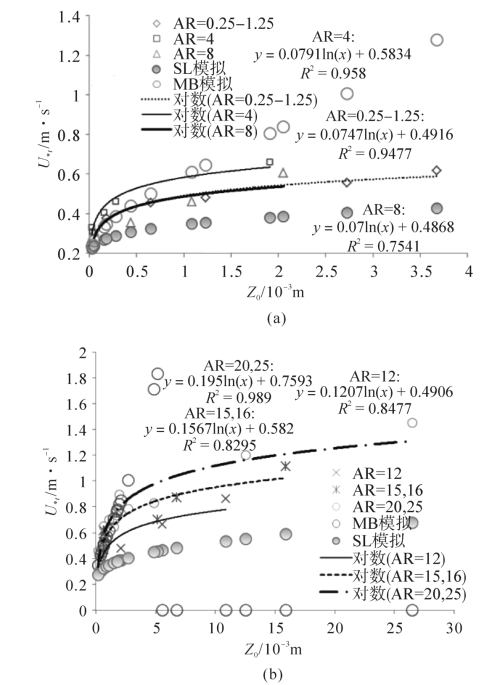
图3-42 不同方向比率AR下起动摩阻风速U∗t与空气动力学粗糙度Z0的关系(梅凡民等, 2020)
3.5.3.2 MB和SL模式的绝对误差及相对误差率的分布
MB模式预测的U∗t分别呈现出与风洞实验结果相对一致、大于实验结果0.2~1.2 m·s-1及预测失效出现零值等3种情形(见图3-42),其分别对应Z0≤1 mm, 1≤Z0≤5 mm,5＆lt;Z0＆lt;30 mm等,这表明MB模式仅适合预测Z0≤1 mm风蚀床面的起动摩阻风速。前人对蒙古高原戈壁草原地区沙尘天气的漏报(Zhou, et al., 2019),与所用的MB模式对U∗t的过高估计有关。
当Z0从10-2 mm增加到26.5 mm时,SL模式预测的U∗t从0.30 m·s-1增加到0.68 m·s-1(见图3-42),其明显低于风洞实验观测结果,特别是在Z0＆gt;1 mm的情形下,这种低估效应更为显著。
图3-43表明当Z0≤2 mm, MB模式的相对误差率约在-20%~40%之间;当Z0＆gt;2 mm时,则MB模式的相对误差率约在80%~100%之间或出现零值(图3-43中出现-1的情形),这意味MB模式在此情形下失效。SL模式的相对误差率约在-50%~-20%之间,相对误差率对Z0的变化不敏感,这表明该模式在不同Z0情形下均会显著地低估起动摩阻风速。
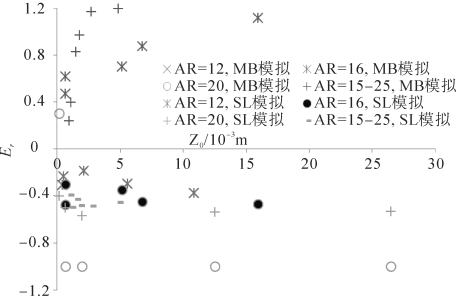
图3-43 MB模式和SL模式的相对误差率Er(梅凡民等, 2020)
MB模式对U∗t的高估、失效及SL模式对U∗t的低估与双边界层的假定有关,而双边界层的成立需要满足粗糙元密度不超过0.1(Marticorena ＆amp; Bergrametti, 1995;Marticorena,et al., 1997)、粗糙元的流向间距与粗糙元高度比值大于3等条件(Alfaro ＆amp; Gomes,1995),本文约有34%的数据不满足此条件,因而出现MB模式高估、失效及SL模式的低估。
另外,SL模式对U∗t的低估也与它所依据的风洞实验数据有关。该风洞实验的Z0约在0.04~1.37 mm之间,对应的阻力分解系数集中于0.5~1.0之间,其缺乏更大的Z0情形下U∗t的数据,因而当Z0＆gt;2 mm时,该模式会出现低估U∗t的情形。
3.5.3.3 基于方向比率、光滑与粗糙床面的空气动力学粗糙度的起动摩阻风速模式
为了说明粗糙床面湍流切应力的分配趋势,这里引入起动摩阻风速比率eff, 它为裸露沙面的起动摩阻风速U∗ts和粗糙床面的起动摩阻风速U∗t的比值,其中实验测量的U∗ts为0.25 m·s-1,裸露沙面的空气动力学粗糙度Z0s为0.05 mm。
图3-44表明在AR(0.25~25)相近或相同的情形下,eff均随着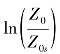
增加而减小,且eff数据与拟合函数的差值均在±0.1 m·s-1,这意味着方向比率整合于起动摩阻风速模式之中,就可以使模拟的误差控制在±0.1 m·s-1以内。
另外,在粗糙元丛状分布的情形下(即对应着孔隙率0.15,0.55,0.75的粗糙床面),这类粗糙床面的eff数值与相近AR情形下密实粗糙元接近(见图3-44),这表明丛状分布或孔隙度对U∗t的影响可用Z0表征。
eff可以表示为式(3-49),其中a′和b′为经验参数(见图3-44):
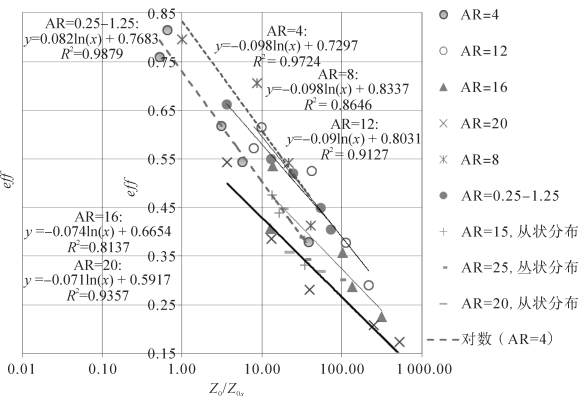
图3-44 不同方向比率下起动摩阻风速比值与空气动力学粗糙度比值的关系(梅凡民等, 2020)
图3-45表明a′和b′分别是AR的一次函数和二次函数。式(3-49)综合地反映了方向比率、Z0与Z0s的比值对eff的影响。由式(3-49)可得到U∗t的函数,它是AR、Z0与Z0s的比值以及裸露沙面的U∗ts的函数(见图3-44)。
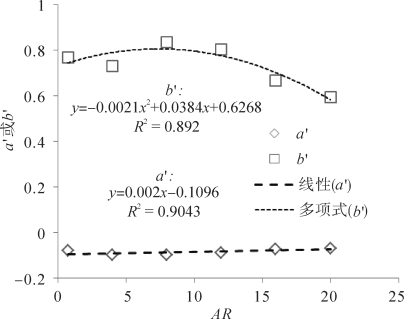
图3-45 式(3-48)中经验系数a′和b′随方向比率AR的变化(梅凡民等, 2020)
和SL模式相比较,式(3-49)的eff所涵盖的范围在0.15~0.85之间,其可以更好地模拟低、中、高粗糙元密度情况下的起动摩阻风速,在模拟沙化的戈壁草原地区跃移起动和粉尘释放强度有更好的潜力。
需要说明的是,为了反映沙化风蚀的草原中不同群落类型的空气动力学粗糙度,著者曾采用数字化群落类型图中建群种平均的高度、覆盖度和单个建群种的方向比率等参数来计算空气动力学粗糙度(梅凡民, 2003)。同样地,可采用式(3-49)来预测不同群落类型的起动摩阻风速,此工作将会在另外的文章中讨论。