1.6.3 动态沉积层与雨滴溅蚀-雨滴诱导薄层水输送模拟
无论是雨滴溅蚀的平地、缓坡或陡坡,均存在单位微元内雨滴分离松散颗粒在临近微元内的沉积。沉积层的形成对下层土壤颗粒的溅蚀具有保护作用,从而影响整个研究单元内雨滴输送强度。雨滴预先分离的溅蚀颗粒沉积层在雨滴溅蚀事件中具有时空变化的特点,因而被称为动态沉积层(Dynamic Depositional Layer (DDL),见 Kinnell (1994))。
为了能够清楚地说明模型原理和数值计算过程(Kinnell, 1994),本书著者结合一个二维床面的雨滴溅蚀-薄层水流悬移输送的方案来展示:①计算网格划分方案如下:二维床面的几何尺寸为100×240 mm2,它被划分为1×1 mm2的方形网格,利用随机数发生器函数模拟2000个雨滴72000次随机碰撞床面的位置。根据5 mm雨滴与0.2 mm沙粒碰撞的观测结果(Kinnell, 1990),设定每个雨滴的扰动范围为9×9 mm2;②为了简化计算做如下假定:流速和流深不随时间变化(如果加上水文模式就可根据降雨强度、土壤入渗率、地表粗糙度等参数来动态地预测流速和流深的变化),这意味着降雨和渗透率是可以比较的;令x′p,d=0.6uw,假定跃移颗粒在薄层水中平均悬浮时间为0.6 s;不考虑溅蚀颗粒抬升高度对x′p,d的影响;当1 mm2内完全被雨滴预先分离的颗粒所覆盖,则每个雨滴可溅射100个颗粒,依此可计算在不同的预先分离颗粒层覆盖度的情景下,每个雨滴能溅射的颗粒数和未被沉积层覆盖土壤的溅蚀强度。
下面为动态沉积层与雨滴溅蚀-薄层水悬移输送模式的原理和模型分析。
为了考虑动态沉积层(DDL)对雨滴溅蚀的影响,式(1-36)中的mp,d可表示为式(1-59):
![]()
其中mpdm是指临近网格被雨滴溅蚀分离、输送并沉积在任意计算网格内(即1×1 mm2)的预先分离颗粒的质量,并假定mpdm 全部被本次雨滴溅蚀输送,Clpd是指在任意网格内mpdm对应的覆盖度,mpde是指任意网格内裸露的土壤被雨滴溅蚀-薄层水输送的质量。
结合式(1-36)和式(1-59)得到式(1-60):
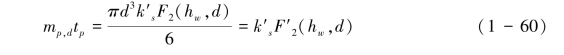
考虑到雨滴溅蚀预先分离的松散颗粒和未被雨滴溅蚀分离土壤颗粒的可蚀性的差异,则它们的可蚀性系数分别定义为kpdm,kpde,结合式(1-59)和式(1-60),可得到式(1-61):
![]()
结合式(1-36)和式(1-61),全面反映薄层水深度、流速和领近雨滴溅射-薄层水跃移输送沉积等对任意计算网格内溅蚀跃移输送强度影响的qp,d可表述为式(1-62):
![]()
整个雨滴谱的流深函数F×(h,r)可表述为式(1-63):
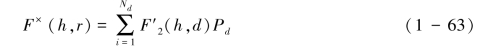 (https://www.daowen.com)
(https://www.daowen.com)
其中Pd为降雨事件中直径为d雨滴的概率。
同样地,还可以把式(1-62)拓展到所有粒径雨滴溅蚀输送的计算。对数值计算而言,通过单雨滴、单颗粒和单个计算网格逐一遍历及迭代,就可计算不同粒径雨滴和土壤颗粒在任意计算网格任意时刻溅蚀输送强度。
数值迭代计算的框架如下:
1)输入已知的降雨和土壤参数:kpdm,kpde,床面各个粒级颗粒的质量/体积百分比,Id,uw,hw,i网格在t=1时Clpd的初始值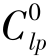 d=0,这意味着雨滴溅蚀前地表没有预先溅蚀分离松散颗粒覆盖。若设置
d=0,这意味着雨滴溅蚀前地表没有预先溅蚀分离松散颗粒覆盖。若设置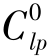 d=1,则意味着所有计算网格为溅蚀分离松散颗粒物质覆盖,
d=1,则意味着所有计算网格为溅蚀分离松散颗粒物质覆盖,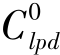 的设置可据实际情形而设定;
的设置可据实际情形而设定;
2)计算网格划分:可根据雨滴特征和土壤特征来设定,也可采用Kinnell(1994)划分网格方案。
3)根据降雨事件的降雨强度I、雨滴谱及降雨持续时间T确定d雨滴的数量,根据雨滴的数量利用随机数发生器函数确定每个d雨滴碰撞位置和次数;根据降雨事件雨滴谱的特征,对雨滴粒径进行循环遍历,确定每个雨滴与床面i网格的碰撞次数和序列;
4)设j网格在t时刻对i网格输入p颗粒的强度为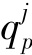 (t),并假定输送颗粒均匀沉积在i网格内,沉积层容重为ρp,t时刻d雨滴从i网格输出的p颗粒强度为
(t),并假定输送颗粒均匀沉积在i网格内,沉积层容重为ρp,t时刻d雨滴从i网格输出的p颗粒强度为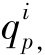 d(t),p颗粒在薄层水的平均水平位移为x′p,d(x′p,d=0.6uw),则沉积层的净厚度可以表示为式(1-64):
d(t),p颗粒在薄层水的平均水平位移为x′p,d(x′p,d=0.6uw),则沉积层的净厚度可以表示为式(1-64):

式(1-64)定义了沉积层厚度,随着![]() 的变化而变化,故该模式能反映动态沉积层对雨滴溅蚀-薄层水跃移输送强度的影响。
的变化而变化,故该模式能反映动态沉积层对雨滴溅蚀-薄层水跃移输送强度的影响。
令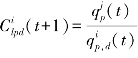 ,利用
,利用![]() 和以前输入的经验参数就可以用式(1-62)计算t+1时刻的qp,d。这样对i网格可以用上一时刻的计算结果递推出下一时刻的计算结果,并形成了循环迭代直到雨滴碰撞结束。
和以前输入的经验参数就可以用式(1-62)计算t+1时刻的qp,d。这样对i网格可以用上一时刻的计算结果递推出下一时刻的计算结果,并形成了循环迭代直到雨滴碰撞结束。
需要说明的是,单雨滴溅蚀质量及输送强度受任意网格内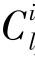 pd,kpdm和kpde的影响。Kinnell(1994)曾经假设在1×1 mm2的网格内当
pd,kpdm和kpde的影响。Kinnell(1994)曾经假设在1×1 mm2的网格内当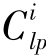 d=1时,则单雨滴溅蚀颗粒数为100(据颗粒粒径和密度可计算质量),这意味着可以根据
d=1时,则单雨滴溅蚀颗粒数为100(据颗粒粒径和密度可计算质量),这意味着可以根据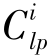 d数值和 kpdm/kpde计算单雨滴的溅蚀-薄层水输送强度。
d数值和 kpdm/kpde计算单雨滴的溅蚀-薄层水输送强度。
5)对二维床面每个计算网格进行遍历循环,就可预测雨滴溅蚀-薄层水跃移输送强度的时空变化趋势。和求解偏微分方程相比较,该过程模型是一种较为简洁模拟溅蚀过程的方案(Kinnell, 2005)。
Kinnell(1994)通过改变uw数值(分别是20 mm·s-1, 40 mm·s-1, 80 mm·s-1)和初始的mpde/mpdm的比值分析了雨滴溅蚀-薄层水跃移输送模型的行为。结果表明,在其他参数一定的情况下,Clpd的数值具有从计算区域上边界向下边界增加的趋势,意味着随着溅蚀进行,雨滴溅蚀分离的松散颗粒的覆盖度向下游增加,且随着薄层水流速的增加Clpd减小。同时,mpde/mpdm的比值也影响到Clpd的大小, 此数值越大则Clpd越大。Clpd随计算上边界的距离、初始的流速和mpde/mpdm的比值的变化行为,说明了上游预分离颗粒在下游堆积的效应以及堆积效应的时刻变化对整个床面的溅蚀输送强度具有显著的影响,这与模式发展的预期效果基本一致。
Kinnell(1994)用溅蚀过程模型模拟降水强度为50 mm·h-1, 坡度为5%、坡长为3 m的斜坡上沙质土壤(其粒径在0.001~4.5 mm之间)的溅蚀过程,结果表明当溅蚀过程达到稳定状态时,径流深度从0.24 mm增加到下坡的1.53 mm, F′2(h,r), Clpd及qs,r(所有土壤颗粒输送强度)均呈现下坡向增加的趋势,且动态沉积层内土壤颗粒粒径分布出现粗化的现象,这反映了雨滴溅蚀-薄层水悬移输送过程中对土壤颗粒的分选特征。
