4.1.2　Bagnold (1941)模式推导及模式评述

4.1.2　Bagnold (1941)模式推导及模式评述

4.1.2.1 风沙边界层特征及研究评述

根据流体边界层理论,Bagnold(1941)总结出中性层结净风情况下风廓线方程(4-2):

其中,U(z)是z高度的风速,U∗为摩阻风速,其代表常应力边界层平均湍流切应力,z0为静止床面的空气动力学粗糙度。和经典的中性层结对数风廓线方程相比较(Nieuwstadt, 1978; Frangi ＆amp; Richard, 1999),式(4-2)预测的平均风速数值约高2倍。

当床面出现跃移时,由于运动沙粒群对气流的反馈作用,风廓线偏离对数律,Bagnold根据风洞实验观测数据,总结出跃移输沙情境下风廓线方程(4-3):

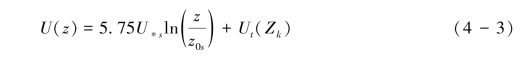
这里U∗s为跃移时的摩阻风速,Z0s为跃移时风廓线焦点/结点高度(focus, kink),所谓焦点或结是指多条风廓线在靠近床面附近的交汇点,意味着不论风强多大,跃移达到稳态时在结点高度风速一致(风动量被大量运动沙粒群吸收所致)。Ut是指在焦点高度对应的起动风速,其可表示为式(4-4):

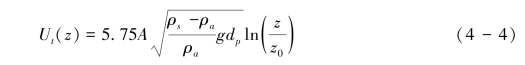
A为经验常数,dp为沙粒直径,ρa,ρs分别是气流和沙粒的密度。式(4-4)是由临界切应力定义和量纲分析推导而来。

需要说明的是,有些学者在实验中并未发现明显的Bagnold结(Belly, 1964; Gerety,1985; Butterfield, 1991)。这个差异与床面特征和边界层的特征有关,也暗示着跃移过程风廓线的复杂性。

Owen (1964)认为跃移层外层的风廓线方程仍然服从对数方程,为式(4-5):

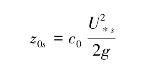
c0为经验常数,约为0.02,Z0s被称为动床的空气动力学粗糙度。最近研究表明,c0取值可以达到0.06(Li, et al., 2004)。

鉴于Owen(1964)模式低估了动床的空气动力学粗糙度,Raupach(1991) 给出了式(4-6):

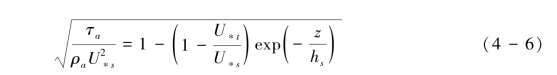
式(4-6)满足基本Owen的基本假定,如τa(0)=ρa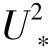t,U∗s=U∗t时,τa=ρa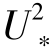s等假设。hs为跃移颗粒的特征高度,其是起跳速度平方(代表颗粒的动能,假定其正比于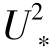s)和重力加速度的函数(即2gh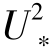s~s)。

湍流动量输运方程为:

据式(4-6)和式(4-7)可得到式(4-8):

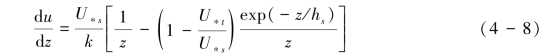
对式(4-8)进行积分,得到式(4-9):

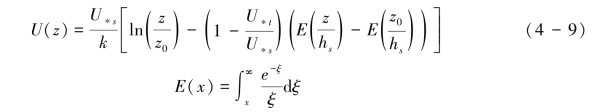
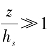
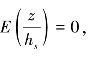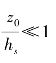对式(4-9)而言,当当时,时,则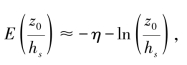η=0.577216

结合式(4-5)和上述近似计算,式(4-9)能被表示为式(4-10):

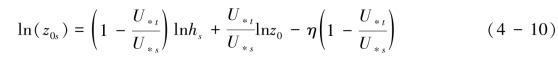
结合对hs的分析,式(4-10)可变形为式(4-11):

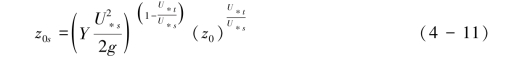
其中Y为经验常数。在床面沙粒为混合颗粒时,U∗t需要迭代计算获得。式(4-11)需要分步计算,先利用对数廓线方程、某高度风速和z0计算初始的摩阻风速,然后代入式(4-11)算出z0s,然后根据此数值用风速廓线方程计算跃移输送时对应的U∗s。

为了简化上述计算,Gillette et al.(1998)利用野外跃移过程中测定的空气动力学粗糙度和量纲分析方法发现,跃移时的摩阻风速可表示为式(4-12):

其中U(10)为10 m高度的风速,Ut根据对数廓线方程由U∗t计算,U∗t计算过程如下(Marticorena, et al., 1997):起动摩阻风速与表土粒度和土壤颗粒的Reynolds数有关,计算采用式(4-13)和式(4-14)。

当0.03＆lt;B＆lt;10时,式(4-13)表示为:

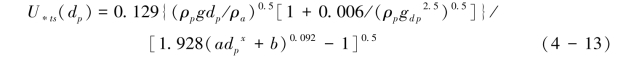
当B＆gt;10时,式(4-14):

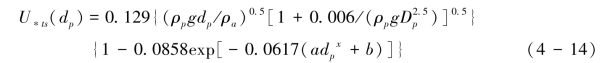
其中B是Reynolds数,B=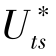·dp/ν,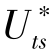是光滑床面的起动摩阻风速,dp是颗粒直径(cm),ν是空气黏性系数,等于0.157 cm2s-1,ρp=2.65 g·cm-3是土壤颗粒密度,a=1331 cm,b=0.35,x=1.56。

当出现粗糙元的时候,风的切应力将在粗糙元和土壤可蚀性组分之间分配,风动量有一部分损耗在粗糙元上,因而提高了可蚀性组分的起动摩阻风速,这时的起动摩阻风速采用式(4-15)~式(4-16)计算:

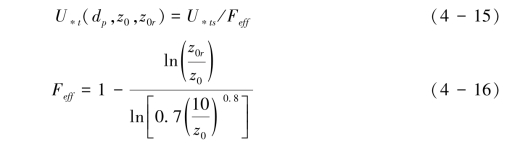
其中z0r为粗糙床面的空气动力学粗糙度,z0是光滑床面的空气动力学粗糙度。

根据式(4-12)就可以计算动床的空气动力学粗糙度和新的U∗s作为计算跃移通量的参数。

当用幂函数拟合风洞实测的跃移风速廓线时,前人发现动床的空气动力学粗糙度可表述为(Dong, et al., 2003)式(4-17):

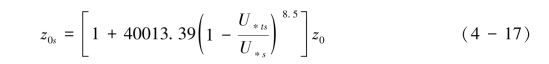
式(4-17)强调在跃移层内,湍流切应力随着高度增加的趋势,而前述公式近似地假定在跃移层上层接近常应力层。

最近,1个跃移层内风廓线的解析式被提出来(Li, et al., 2004)。该解析模式的发展是从跃移层内跃移颗粒群的粒载切应力τp(grain-borne stress)入手来求解,其原理与Owen (1964)和Raupach (1991)模式相似,τp表述为式(4-18):

这里mp为单个沙粒的质量,np是z高度沙粒的个数(均一粒径,在跃移达到稳定状态时,上升的颗粒和下降颗粒数相等),为z高度上升沙粒平均垂直速度,和分别是上升和下降沙粒的平均水平速度。式(4-48)可变为无量纲形式:

这里τp(0)代表床面的湍流切应力,其他指标相同。按照Owen(1964)的定义τp(0)可表示为式(4-20):

假定,则有式(4-21):

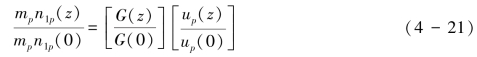
在式(4-21)的推导中,采用了的定义及稳恒状态时上升颗粒数等下降颗粒数的假定。

考虑跃移层内不同高度输沙质量的负指数衰减趋势,则可以推导出式(4-22):

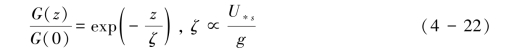
ζ是沙粒起跳高度的数量级。

忽略气流对沙粒起跳的垂向作用力,则可推导出式(4-23)这里hs是跃移颗粒平均跃高:

式(4-23)进一步可整理为式(4-24):

计算起跳沙粒的弹道轨迹上z高度的速度,则有式(4-25)和式(4-26):

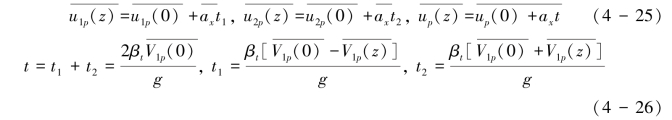
这里βt为经验系数。

整合式(4-2)、式(4-25)~式(4-26)则可推导出跃移层内风速廓线方程式(4-27):

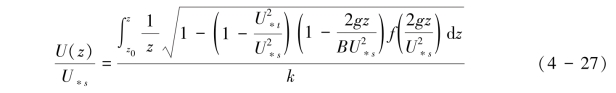
这里B为经验系数,来自实测跃移风廓线数据的拟合。

通过拟合实测的跃移风廓线数据,Li et al.(2004) 发现风廓线可分为两个区间,在跃移层外层风廓线方程符合公式(4-5)而在跃移层内层风廓线符合式(4-27),这时Bl=0.45。当U∗s略高于起动摩阻风速时,则跃移风廓线全段可近似地用对数风廓线来代替(Butterfield, 1999)。

敏感性实验表明(Li et al., 2004),式(4-5)和式(4-27)所预测的跃移风廓线特征对c0和Bl及Bl/c0是敏感的,当摩阻风速在0.25~1.25 m·s-1之间,Bl/c0＆gt;10,则预测的风廓线不出现Bagnold结,这与前人实测的风廓线数据一致(e.g.Belly, 1964; Gerety,1985; Butterfield, 1991; Bauer, et al., 2004 )。

和式(4-9)、式(4-11)相比较,式(4-27)有几个优点:能预测当z=hs时,τa=ρa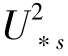而前者不能预测此趋势(即不能满足基本假定:在跃移外层,气流切应力等于气流密度与摩阻风速平方);能预测在跃移层内湍流切应力随着高度增加而增加直至跃移层顶,而前者所预测的递增趋势未能达到理论假定的条件。最近大涡模拟的风沙跃移过程表明,Raupach (1991)的模式接近大涡模拟的结果(Dupont, et al., 2013),这说明跃移层内风廓线分布的复杂性。

Raupach (1991)的风廓线模式与Li et al.(2004)模式所依据的原理相似,造成模拟结果的差异主要原因是前者把跃移颗粒群对气流反馈作用比拟为粗糙元对气流的阻滞作用,而粗糙元对气流的阻滞作用和跃移颗粒群对气流阻滞作用机制不完全相同。从本书第3章粗糙元覆盖床面的风廓线数据来看(如图3-10),粗糙床面的风廓线均不存在Bagnold结特征,暗示着粗糙元对气流的阻滞效应与跃移颗粒群有一定差异。

最近一个新的观点是,跃移层外层风速廓线方程中的Kármán 常数是一个随着跃移通量变化的变量(Li, et al., 2010;Sherman ＆amp; Li, 2011),这进一步暗示跃移层内风廓线的复杂性。

上述的研究把风沙边界层的特征看成是一个平均的过程。近年来,研究人员从湍流角度对风沙过程进行研究,取得了一系列的新认识(e.g.Sterk, et al., 1998; Leenders, et al., 2005; Baas ＆amp; Sherman, Baas, 2006, 2008; Dupont, et al., 2013; Bauer, et al.,2014),这些研究有助于从新角度理解风沙跃移的机理,也有助于从湍流输送的视角重新理解Bagnold模式。

4.1.2.2 跃移通量模式的推导

Bagnold (1941) 对多样性的沙粒输送轨迹进行了抽象,假定研究的沙粒是均一的球形颗粒且在所有的风强下都有同样的轨迹即特征轨迹(Characteristic path)。特征轨迹对应的平均起跳高度被认为是风廓线的Bagnold焦点高度。

假定单沙粒的质量为mp,起跳的水平速度和垂直速度分别为upl和Vpl,入射水平和垂直速度(或称为碰撞速度)分别为upi和Vpi, 水平跃距为l, upl被认为很小趋近于零(这个假定是不对的,仅对部分溅射颗粒成立),跃移通量为Fh,则气流输送沙粒在单位时间、单位长度、单位宽度损失的动量为MNL可表示为式(4-28):

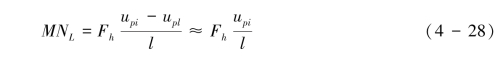
MNL 被认为是运动沙粒对气流的阻滞效应,其等价于湍流切应力对沙粒输送释放的动量,因而式(4-28)可转换为式(4-29):

Bagnold(1941)认为式(4-29)左边的第二项是与g/Vpl成正比,则式(4-29)可变化为式(4-30):

尽管前人没有详细交代上述关系成立的理论或观测依据(Bagnold,1941),本书著者认为沙粒特征轨迹受两个因素影响,一是重力且重力超过气流对其产生的上举力而使得跃移颗粒回到床面上,二是Vpi和气流拖曳力τ有关,它们决定了颗粒起跳高度和在气流中飞行的时间和距离,这可以从量纲分析来获得。至于Vpi和气流拖曳力τ的关系可能是十分的复杂的。Bagnold(1941)假定Vpl=BgU∗s,其中Bg为无量纲的经验常数,并假定其仅与沙粒的本质有关,于是式(4-30)可调整为式(4-31):

考虑到室内和野外测量的输沙强度包括蠕移颗粒的贡献,而蠕移颗粒输送强度与气流拖曳力τ无关。通过比较实测数据和模式预测的数据差异,Bagnold(1941)认为蠕移输送通量约为测定的输沙通量的1/4,于是式(4-31)可表示为式(4-32):

考虑到沙粒粒径及分布对跃移通量的影响,式(4-32)被调整为式(4-33):

式(4-33)即为经典的Bagnold跃移模式, 其中均一沙时,Cg=1.5,天然分选的沙丘沙Cg=1.8,广泛粒径分布的混合沙Cg=2.8,dp研究沙粒的平均粒径,Dp=250 μm为参照粒径。

4.1.2.3 Bagnold跃移通量模式的表现

Bagnold跃移模式首次提示了跃移通量和摩阻风速的定量关系,这是为后续半经验模式的发展奠定了基础,风沙跃移定量模拟研究的开创性工作。然而,该模式只有满足均一沙粒、稳恒流场、平坦干燥的沙面等非常理想的条件才能保证良好的精度(Sherman, et al., 1998),而这些条件只有在室内风洞中才有可能近似地满足。野外风蚀过程中,沙粒粒径分布的异质性、水分差异、不断变化的风速和风向(特别是阵风事件)、起伏不定的沙面等环境因素会造成模式预测的误差。多变环境下的海岸风蚀观测的研究表明利用Kármán 系数代替Kármán 常数来预测的摩阻风速和跃移通量的关系更接近Bagnold 跃移模式。Bagnold跃移模式优于其他的半经验模式,尽管如此,模拟的跃移通量和观测数值的相关系数的平方仅为0.50,模式的不确定性是很明显(Sherman, et al., 2011)。

值得注意的是,通过实验观测的结果来评价跃移模式也存在一定的不确定性:一是湍流观测和数据处理中的误差。室内或野外实验利用梯度风速数据来计算摩阻风速还存在较大的不确定性,这和计算平均风速的时长有很大的关系,在高时间分辨率情形下,摩阻风速的变化是混沌的(e.g.Baas, 2008),只有较长的时间尺度才可能获得稳定的摩阻风速数据。另外,风洞实验条件下,拟合对数廓线还存在很大的不确定性,拟合区间微小变化可导致拟合的摩阻风速的显著变化,此情形如同在粗糙床面的风廓线特征(读者可参考本书3.3的研究内容和结果)。野外实验风廓线数据的拟合也存在类似问题。另外,野外风廓线数据分析还需要考虑大气层结的影响(e.g.梅凡民等, 2006; Mei, et al., 2006),而这常被野外风速梯度观测数据的拟合所忽略。值得庆幸的是,超声风速仪可直接测定三维/二维的湍流信息,其摩阻风速可直接计算而不需要通过风速梯度拟合,这就规避了传统数据拟合的误差。二是跃移通量的观测误差。跃移通量观测中存在的主要问题是不能或没有分离跃移和蠕移颗粒,除少数研究外(e.g.Bagnold, 1941),大量的风沙观测都是基于输沙率概念,都没有采用专门装置来分离跃移和蠕移组合,而蠕移输送可能和摩阻风速无直接关系。跃移通量是根据输沙断面上不同高度的输送强度来计算,而实际的输沙质量廓线不完全服从负指数函数或幂函数,拟合的不确定性可能在床面附近达到最大,但此现象还未引起研究者的重视。雨滴溅蚀输送强度的理论分析方法可能为跃移强度的观测提供借鉴(见本书第1章1.7节的内容)。另外,不同积沙仪的积沙效率也存在差异。野外气流和流沙的异质性因素如粒径及粒径分布差异、水分等也给数据分析和解释带来很大的困难(Davidson-Arnott ＆amp; Bauer, 2009; Ellis, et al., 2012; Poortinga, et al.,2015),这给因素模式的验证带来不确定性。至于风场的不稳定性的问题,本章在4.2专门讨论,在此不再赘述。

关于Bagnold模式有2个令人困扰现象值得思考:一是在模式推导过程中涉及的沙粒垂直起跳的假定与实际情形相悖(e.g.Nalpanis, et al., 1993; Zou, et al., 2001; Dong,et al., 2002a; Zhang, et al., 2007),但此假定似乎并没有影响到模式可靠性,这是否意味着微观过程与宏观过程缺乏直接联系。这个现象引出问题是建立基于复杂微观机理的跃移模型是否是重要的和必要的。二是最近基于大涡模拟的风沙跃移研究结果也表明(Dupont, et al., 2013),模拟的无量纲摩阻风速与跃移通量的关系与Bagnold模式较为接近,而这一结果又与其他研究结果矛盾(e.g.kok ＆amp; Kenno, 2009),这意味着Bagnold模式的可靠性似乎还没有定论。