1.7.1　溅射距离分布理论分析

1.7.1　溅射距离分布理论分析

1.7.1.1 矩形溅蚀盘/杯情景下的溅射距离分布(溅蚀源区为矩形)

自从开展雨滴溅蚀观测研究以来 (Ellison,1947),研究人员设计了15类雨滴溅蚀测量的装置(Fernández-Raga, et al., 2017),它们分别为溅蚀杯、溅蚀漏斗、溅蚀瓶杯、溅蚀板、溅蚀槽、溅蚀帘、溅蚀屋、Morgan 盘、Leguédois 盘、墨汁或放射性示踪、溅蚀棍、溅蚀盒、溅蚀-径流分离盒、方向溅蚀盒、T形杯保留等。雨滴溅蚀装置的设计除了考虑具体应用场景外,还有一个需要考虑的是装置的几何形状、尺寸和观测精度的关系,包括土壤溅蚀源(溅蚀源装置)与接收装置的几何形状、尺寸及相关的溅射距离等问题。Farrell et al.(1974) 从单个溅射颗粒运动轨迹出发,提出了环形和矩形溅射装置的形状修正因子表达式,但由于对溅射颗粒的空间分布规律了解有限,限制了其理论分析的应用。在认识溅蚀密度指数分布规律的基础上(Poesen ＆amp; Savat,1981; Savat ＆amp; Poesen,1981; Riezebos ＆amp; Epema,1985),Van Dijk et al.(2002)发展了一个溅蚀分离与输送的数学模型来解释溅蚀输送的实验数据,并提出了矩形和环形溅蚀装置的几何修正参数。下面对他们的理论进行总结和分析。

引入溅蚀密度函数Mpiont来表征单位源面积、径向距离为r的单位靶面积(单位接受面积或单位沉积面积,这里假定溅射颗粒沉积到接受单元内,不再反弹起跳)的溅射质量(单位为g·m-4),其可表示为式(1-66):

其中S为单位面积雨滴溅蚀分离率(g·m-2),λ为质量权重平均的溅射距离(m)。式(1-66)来自前人观测到的溅射距离负指数分布趋势(e.g.Riezebos ＆amp; Epema,1985)。但应该看到,溅射负指数分布趋势在较大尺度上才能近似成立。在Riezebos ＆amp; Epema(1985)的实验中,最小径向距离为5 cm,这意味着5 cm以内溅蚀密度随径向距离的变化趋势是否符合式(1-66)还不清楚。也就是说,欲了解准确的溅蚀密度函数还需要从微小的源面积、微小靶面积入手利用微积分原理来分析、推导溅蚀密度函数。

先推导一个基于无限长直线边界的一维溅蚀密度函数。在直角坐标系中,溅射源任意微条带(简称源微条带)是由沿y方向(该方向可无限延伸)的dy和x方向的dx围成,x方向代表溅射密度函数的变化方向,源微条带的坐标为(0,y)。和源微条带相联系的靶微条带的坐标为(x,0),则源微条带对(x,0)处溅蚀密度函数的贡献为式(1-67):

其中Ξstp(x)表示单位宽度源微条带、单位靶面积的溅蚀强度(g·m-3)。对式(1-67)的右边进行积分,可得到式(1-68):

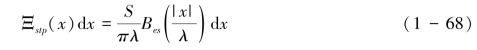
其中Bes为Bessel函数(Abramowitztion ＆amp; Stegun,1965)。式(1-67)表明一维情形下溅蚀密度函数不符合负指数分布,即式(1-66)是近似的。在|x|较大的情形下,溅蚀密度函数服从负指数分布(Van Dijk et al., 2002)。

为了理解溅蚀密度和溅蚀输送强度的关系,需要界定源微条带和靶微条带的边界。对式(1-68)在x与∞之间进行积分,得到每单位源宽度、每单位边界长度的溅蚀输送强度式(1-69):

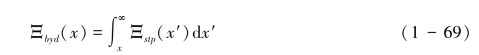
这里x′是积分变量。溅蚀输送率q为单位边界长度的输送强度,可表示为式(1-70):

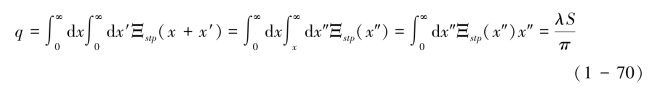
这里x″=x+x′,公式右边的积分计算是根据数学手册而来(Abramowitztion ＆amp; Stegun,1965),q为穿过无限长直线边界的溅蚀输送强度。鉴于实验用溅蚀盘不是无限大,假定溅蚀盘具有有限宽度w和无限长度,则穿过(0,w)的输送率可表示为式(1-71):

这里的q(w)可看作是溅蚀装置测量的溅蚀输送强度,而式(1-70)中可看作是理论上的溅蚀输送强度,二者的比值L可表示为式(1-72):

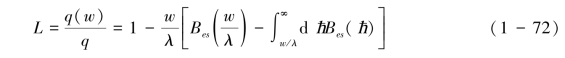
这里ħ=x/λ,L为溅蚀装置有效宽度w的修正系数。式(1-72)可近似化简为式(1-73):

据分析(Van Dijk et al., 2002),当1≤w/λ≤100时,L＆lt;0.01; 0.2≤w/λ≤1时,L＆lt;0.1,这意味着当溅蚀装置具有无限长度时,宽度超过平均溅射距离后,该装置测量的误差可忽略。但是实际的采样盘也不具有无限长度,因而需要考虑在此情形下溅蚀装置的修正系数(后面在二维情形讨论)。

上述情形可类比为溅蚀源是无限大而一侧的接收区为长度无限长而宽度在(0,X)之间的区域,则在ΔX=(x1,x2)之间的q(ΔX)可表示为式(1-74):

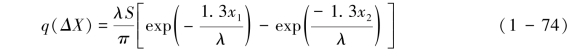
需要说明的是,式(1-73)和式(1-74)仍然是近似的,不适合应用到面积太小的溅蚀源或接收区。

在二维情形下溅蚀装置均是有限长度和有限宽度,需要讨论测量和理论溅射输送强度的关系。量纲分析显示,对一个方形溅蚀盘而言,影响其测定溅蚀输送强度的变量分别是边长Å,B和λ等,无量纲的尺度分别是Å/λ,B/λ或Å/B。

这里发展基于迭代计算的一个矩阵模型来模拟不同的Å/λ 和Å/B情境下,测定的溅蚀输送强度和理论计算真值的比率作为修正矩形溅蚀源区-有限/无限接收区的修正因子,具体计算过程如下(本书著者对Van Dijk et al.(2002)计算过程分析后,重新整理以便于计算机编程的需要,并对原文中的笔误进行了纠正):

1)参数输入:S=1,设定Å,B和λ的初值,让Å,B的初值与λ的比值从较小的数值如0.1开始运行;

2)确定溅蚀源区和接受区的计算范围,划分并标记计算网格(见图1-5):根据Å,B的初值确定土壤盘的大小(溅蚀源区),以5Å 和5B为计算网络边界,溅蚀源区右侧为溅蚀接受区,其中栅格接受区(Screen)是指与溅蚀盘等长而宽度为5Å(图1-5中仅为示意,并不是其真实的宽度),边界接受区(Corner)与格栅接受区同等宽度,但其长度为5B(同样地在图1-5中仅是示意而非真实的比例)。为了计算方便,在确定溅蚀源区和接受区的基础上,它们被划分为单位面积网格。需要说明的是,当溅蚀盘被置于平坦的地面时,土壤颗粒溅蚀在各个方向大体上是均一的(见Furbish et al.(2007))。Van Dijk et al.(2002)在计算网格设定与划分时,默认以溅蚀源区右侧的接受区为计算区域,这样处理的好处在于能够减小计算量。需要说明的是,计算网格区间还可以更大。

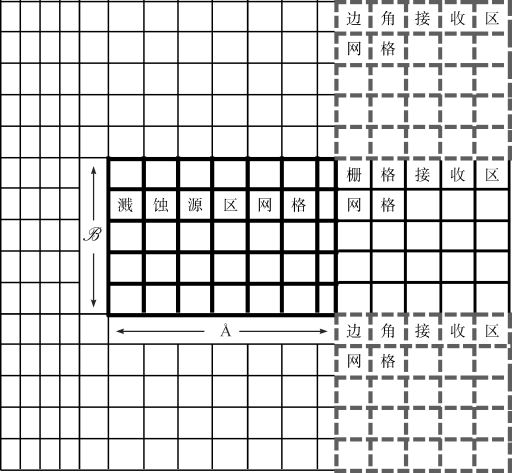
图1-5　迭代计算的网格划分示意图

溅蚀源区网格以粗实线为边界,格栅接受区(Screen)以细实线为边界,边角接受区(Corner)以粗虚线为界,网格边界以5Å和5B为界,本图依据Van Dijk et al.(2002)图4修改。

这里的溅蚀接受区分为3个类型:栅格接受区(Screen)被看作是有限接受区;栅格接受区+2个边角接受区(Corner)被认为是无限接受区;栅格接受区+1个边角接受区相当于一个水平方形的接受板+三面环绕的垂直接受板。

3)采用式(1-68)分别计算溅蚀源区内每一个网格对与其他网格的溅蚀沉积质量、对有限接受区和无限接受区的每个网格的沉积质量,然后分别对溅蚀源区-有限接受区、溅蚀源区-无限接受区计算沉积总质量与网格数的比值(Rg);采用式(1-74)计算观测的溅蚀输送率、观测的溅蚀输送率与理论值的比率(L)(理论溅蚀输送率用式(1-70)计算);

4)若Rg＆gt;1%, 则让Å和B数值加倍直到满足要求;

5)输出Å,B,Å/λ,Rg和L的计算结果。

从图1-6可以看到,对有限接受区而言,当Å=10λ时,Å/B数值对L影响不大且接近0.9,当Å=100λ时,L=1,这意味溅蚀盘宽度为平均溅射距离100倍时,溅蚀盘的几何尺寸效应消失(见甲图);对无限接受区而言,只要Å=5λ时,Å/B数值对L影响不大1,Å=10λ时,溅蚀盘的几何尺寸效应消失(见乙图)。

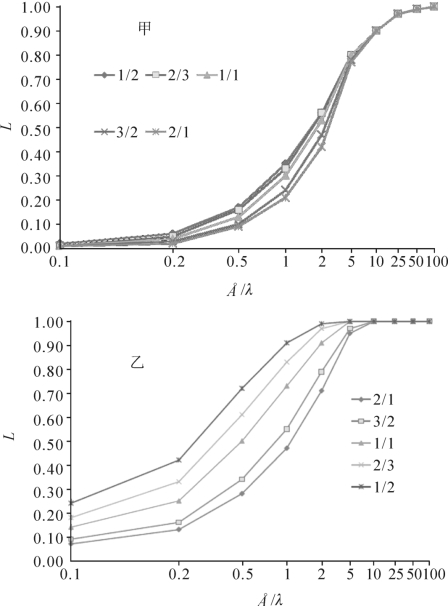
图1-6　溅蚀盘的几何尺寸与溅蚀测量修正系数的关系

不同系列数字为Å/B的数值,λ 为平均溅射距离,L为修正系数Å,B为溅蚀盘的几何尺寸,(甲)代表有限接受边界,(乙)代表无限接受区,本图是根据Van Dijk et al.(2002)文中表1数据绘制

综上所述,真实溅射距离密度函数服从Bessel 函数,在溅射距离较大的情形下,它近似服从负指数分布。矩形溅蚀盘只有满足一定几何参数和接受区几何参数,才能获得和实际一致的测量结果。

1.7.1.2 圆形溅蚀盘/杯情景下溅射距离分布趋势(溅蚀源区为圆形)

Van Dijket al.(2002)采用了和矩形区域相似的数值计算来分析圆形溅蚀杯半径R与平均的溅射距离之间的比值对修正系数Lr的影响,发现R/λ为0.1时,Lr接近0.9,R越大则修正系数越小,这与矩形溅蚀杯的几何尺寸效应有着显著的区别,而后者是宽度愈大则测量误差愈小。这意味着圆形溅射杯和矩形溅蚀杯的几何效应截然相反。圆形溅蚀杯的修正系数可表示为式(1-75):

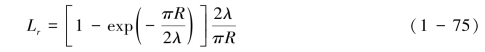
需要说明的是,上述的数学推导过程(1.7.1.1~1.7.1.2)仅适合平坦床面雨滴溅射的情况,对斜面上溅射距离分布是不适合的,且推导更加复杂。Van Dijk et al.(2002)强调了目前坡地上溅射距离负指数分布还有很大的不确定性。

1.7.1.3 土壤团聚体溅射距离分布(圆形溅蚀杯-同心圆接受区)

为了理解土壤团聚体溅射距离的分布趋势,Legue′dois et al.(2005) 推导了在圆形溅蚀杯-同心圆接受区情境下的溅射距离分布函数,具体推导及验证过程如下:

据式(1-66)可推导单位源区长度、单位靶面积单位降水量下雨滴溅蚀质量marc(见图1-7)为式(1-76):

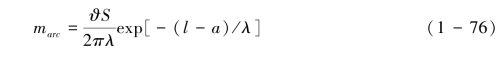
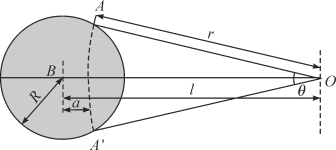
图1-7　圆形溅蚀杯-同心圆接受区及积分运算示意图

灰色区域代表溅蚀杯,O代表同心圆环形接受区的中心,l为径向距离,ϑ为弧长AA′对应的角度,根据Legue′dois et al.(2005)文中图4绘制。

对式(1-76)在整个圆周上进行积分,得到式(1-77):

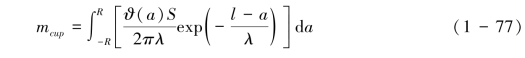
其中mcup为单位降雨量、单位靶面积溅蚀杯中溅射颗粒沉积在O点的质量,ϑ(a)是关于a的隐函数,这里用它的均值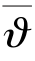近似地代替它,则对式(1-77)积分可得到式(1-78):

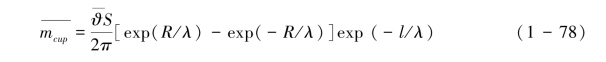
这里上划线所标记的量为均值。通过数值实验发现,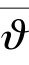可表示为式(1-79):

由式(1-77)、式(1-78)、式(1-79)可得式(1-80):

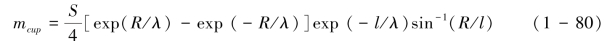
式(1-80)表明在溅蚀杯-同心圆接受区情景下,溅射距离的分布不同于以前讨论的负指数分布,而是一个由径向距离、sin-1(R/l)等变量构成的复合函数。

环形区域被分成1×1 mm2的网格,采用快速傅立叶变换方法来对式(1-80)的可靠性进行数值验证,结果表明其精度超过99%。式(1-80)为理论推导并经数值验证的溅蚀质量分布模式。

在溅蚀杯-同心圆接收区的情景下,测定的单位降雨量下径向距离为li的第i 环带上沉积的溅蚀质量mi(li)可定义为式(1-81):

这里Mi为测定的第i环带内在宽度wi内沉积的溅蚀颗粒质量,pr为降雨量。

对式(1-80)两边取对数进行线性处理,采用最小二乘法拟合公式中待定的S和λ,就可获得具体的雨滴溅蚀情景下的平均溅射距离。

图1-8反映了4类不同质地土壤的不同粒级颗粒的平均溅射距离分布特征:①和其他土壤类型不同,沙土溅射距离分布具有单峰特征,最大溅射距离为22.6 cm,对应几何平均粒径为125 μm。和中沙和粗沙相比较,粉细沙是最易被雨滴溅蚀的颗粒且能在相同的雨滴动量的情况下被雨滴溅射得更远;和粉沙和黏粒相比较,粉细沙颗粒之间较小的黏滞力使得雨滴分离颗粒所消耗的动能是最少的,从而导致粉细沙可获得更多的动能从而有最大的溅射距离。至于平均的溅射距离是否和起跳角度有关,由于目前还没有具体数据支撑;②粉壤质土壤、黏粉壤质土壤、黏壤质土壤的溅射距离分布具有双峰特征,粉壤质土壤第一峰值的溅射距离为20.2 cm, 对应的平均粒径为125 μm,第二个峰值的溅射距离为19.1 cm,对应的平均粒径为350 μm;黏壤质土壤双峰对应的溅射距离低于粉沙质土壤,这意味着随着黏粒和细粉沙含量增加,土壤黏滞力提高而导致相同粒级颗粒的溅射距离下降。粉黏质土壤没有很明显的双峰特征,这与去除了相关系数低的150 μm和200 μm粒级的溅射距离数据有关,也暗示了雨滴在分离、溅射黏结性土壤团聚体的复杂性;③溅射颗粒中未发现小于0.1 μm的组分,意味着细黏粒的溅蚀需要消耗更多的雨滴动能。Legue′dois et al.(2005)的观测数据表明模拟降雨的最大粒径不超过3 mm(雨滴粒径偏小), 降速不超过7 m·s-1,其降雨动能可能不足以分离细黏粒并导致其起跳(也有可能是细黏粒被分离但雨滴动量不足以被溅射到最近的沉降测量区);④粉黏质土壤中细沙的溅蚀输送强度不符合式(1-80)所揭示的分布趋势,暗示着某些固结性/半固结土壤的溅蚀输送强度及溅蚀距离分布不符合指数或式(1-80)复合函数;⑤对黏壤质和粉黏质土壤而言,粒径小于50 μm颗粒的溅蚀距离约在7~10 cm之间,较低的溅蚀距离可能有两个原因:a)黏滞力很大的颗粒需要大雨滴来分离和携带,而碰撞后大雨滴运动距离较短(Legue′dois, et al., 2005);b)这个粒级颗粒未被雨滴分离而是和其他粒径颗粒形成的土壤团聚体一同被雨滴溅射的,此过程中雨滴仅分离、破碎大团聚体为次一级的团聚体,从图1-8可看到,同一个土样0.2~50 μm的颗粒具有近似的溅射距离则是佐证(后一种原因是本书著者观点)。

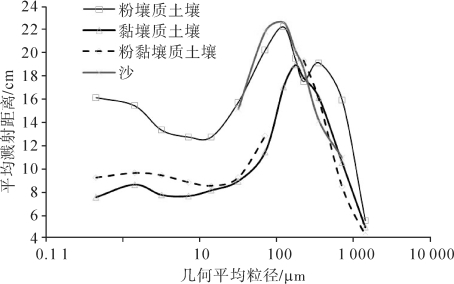
图1-8　溅蚀几何中值粒径与平均溅射距离的关系

根据Legue′dois et al.(2005)文中表3数据绘制,并舍弃了拟合相关系数的平方小于0.65的数据。

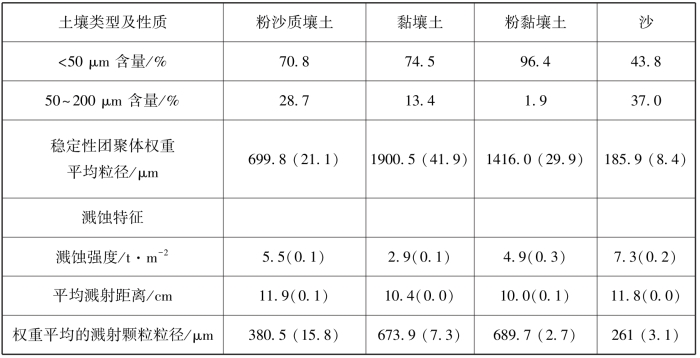
从表1-1可看到,雨滴溅蚀强度随土壤质地的变化是十分复杂的,大体上它随着黏粒含量增加而降低,但粉黏质土壤和黏壤质土壤不完全如此,前者的黏粒含量与后者相差很小(不到1%)但溅蚀强度要比后者高60%,从其他粒级颗粒对比中也找不到原因,如粉黏质土壤的粉沙+细沙含量要显著地小于黏壤质土壤,而这个粒级颗粒是最易被雨滴溅蚀的。鉴于上述结果基于统计平均,而统计平均结果和实验次数(不确定随机因素的影响)有关,从Legout et al.(2005)文中可看到,粉黏质土壤溅蚀测试次数为3次,少于黏壤质土壤,因而本书著者猜测这两类土壤溅蚀强度的差异与实验随机误差有关。

图1-8显示土壤类型对不同粒级颗粒的平均溅射距离分布特征有明显的影响,但整个土样的统计结果显示,上述4类土壤平均溅蚀距离无显著差异,均在10~12 cm之间(见表1-1),这也与4类土壤溅蚀输送强度的径向分布均近似地服从负指数分布相一致(见Legout et al.(2005)文中的图2及Legue′dois et al.(2005)文中的图5, 图6)。

沙样的权重平均溅射颗粒粒径是最小的(见表1-1),其次是粉壤质土壤、黏壤质土壤、粉黏壤质土壤,此溅蚀特征随土壤质地变化是复杂的,似乎受黏粒含量影响,但同时还存在其他不明因素的影响,其数据的可解释性有待提高。

本书著者发现(表1-1数据),和土壤质地的相关参数相比较,稳定性团聚体的平均粒径与溅蚀输送强度及平均溅蚀颗粒粒径有一致的变化趋势:随着稳定性团聚体平均粒径从186 μm增加到1900 μm,溅蚀输送强度从7.3 t·m-2下降到2.9 t·m-2。

表1-1　粉沙质壤土、黏壤土、粉黏壤土和沙等的雨滴溅蚀特征(数据来自Legout et al.(2005)文中表1,表2,降雨强度为30 mm·h-1)

续表

综上所述,溅蚀输送强度的密度函数表明(Van Dijk, et al, 2002; Legue′dois, et al.,2005),溅蚀输送强度密度函数结构、类型与溅蚀源的几何尺寸、接收区的几何尺寸、土壤质地、土壤稳定性团聚体的平均粒径等因素有关。在厘米级尺度上,密度函数近似地服从负指数函数分布,但具体的经验参数因土壤类型而异(e.g.Legout, et al., 2005; Legue′dois, et al., 2005)。

上述研究是在人工模拟降雨和裸露土壤上进行的,在天然降雨下、在坡地和植被覆盖下溅射距离分布情况,需要进一步总结和分析(见1.7.2)。