3.2.2　基于湍流结构的风沙颗粒起动动态演化模式

3.2.2　基于湍流结构的风沙颗粒起动动态演化模式

经典的流体力学把光滑固壁区流体自壁面而上分为3个区域:黏性底层、过渡区域和对数区域等。黏性底层被看作是流体运动学特征主要受分子黏性控制的层流而对数区为常应力层。20世纪50年代以后,流体力学研究逐步地发现,黏性底层并不是完全稳定的层流而是间歇性变化的湍流,特别是斯坦福大学关于边壁区湍流猝发现象的发现,完全改变了人们对黏性底层的认识。即在流体边界层的黏性底层,周期性存在低速条带、猝发、高速下扫等流向湍涡结构,每一次低速条带猝发和高速流体下扫等过程都伴随着湍流动量的急剧释放。不但黏性底层存在着湍流动量周期性爆发过程,而且在对数区也存在着猝发-下扫结构。流体力学把边壁区准周期的这类湍流动量爆发事件和湍流结构称为相干结构,相干结构被看作是湍流动量释放的最重要形式。湍流过程被看作是随机脉动和有组织的湍流结构交替出现过程。

象限分析方法被用来区分湍流结构和随机脉动。象限分析的“洞”为区分二者的湍流脉动的阈值,一般是湍流平均雷诺应力标准偏差的倍数。若瞬时运动应力的绝对值超过这一阈值,则此脉动事件属于湍流结构事件。这里以风沙两相流实验风洞的边界层结构来模拟风沙颗粒起跳的动力学机制。

根据流体力学的边界层理论和风沙两相流输运的规律,把实验风洞的风沙边界层自床面以上依次划分为边壁区、跃移层和主流区(见图3-6)。风沙边界层内的边壁区是沙粒群浓度最大、速度最小和气流流速最小的区域,这里汇集了大量的蠕移颗粒和低速的跃移颗粒,同时也是湍流相干结构发生、发展和消亡的区域,整个跃移层内由于大量运动沙粒群吸收了湍流动量,风廓线偏离对数律;主流区是风沙两相流动量直接或间接来源,风速廓线服从对数律。

图3-6　风沙边界层示意图(U∞与Ut分别边界层风速和沙粒起动风速)(梅凡民,2011)

根据前人对高雷诺数壁面湍流结构的研究可知(Hunt ＆amp; Morrison, 2000),边壁区湍流结构的生成主要是风沙边界层上部(这里定义为主流区)动量下传的结果。来自主流区湍涡经过冲击壁面、湍涡被壁面阻塞、被阻塞的湍涡之间、湍涡与壁面相互作用、诱发低速上举的条带、上升的低速条带破裂、湍流边界层的内层诱发壁面下扫结构。下扫事件结束后再经过平静期后,将会继续触发新条带和相干结构,这会不断地把主流区湍流动量传递到浸没在壁面的沙粒。这种湍流结构的生成模式被称作是自上而下模式。这里以自上而下的湍流结构模式来建立风沙两相流的演化模式。

按照风沙边界层动量守恒的原理,可以建立起跳沙粒群动量和湍流动量的基本关系式(Owen, 1964)(3-5):τt,τs(z),τa(z)分别是风沙边界层主流区湍流的总动量(或雷诺应力)、跃移层z高度处运动沙粒群的动量(或雷诺应力)和湍流的动量(或雷诺应力)。

目前对风沙两相流平衡的定义还不是十分明确,这里定义为主流区湍流动量大部分转化为运动沙粒群动量,而余下的跃移层内的边壁区湍流的动量τa(0)不足以使静止沙粒起跳,于是风沙两相流平衡时刻ti定义式为:

U∗t代表临界起动摩阻风速,反映了使沙粒由静止状态而起跳所消耗最小湍流动量,ρ为空气密度。Bagnold认为当风沙输运达到平衡时,τa(0)=0;而按照Owen的观点,τa(0)=ρ·U2∗t,如果把跃移层内起跳沙粒群看作静止床面的粗糙元,而起跳的沙粒群相对于气流而言还是稀相,从湍流动量分配机制来看,床面附近湍流雷诺应力为零的可能性很小,故以式(3-6)作为风沙两相流平衡状态的定义式是合理的。

这里假定ti+1时刻主流区大量动量下传,首先边壁区出现低速上抛事件,由于边壁区沙粒群对湍流动量响应的滞后性(可以认为τs(ti+1)=τs(ti)是成立的),风沙两相流失衡,这时气固两相流的定量关系式为:

ti+2时刻上抛事件演化成下扫事件,跃移系统继续调整且处于失衡状态,对应的气固两相流的定量关系式为:

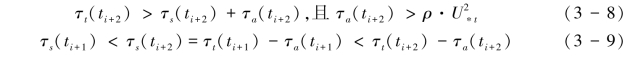
式(3-9)意味着ti+2时刻的运动沙粒群动量与边壁区湍流动量是不平衡的,但与ti+1时刻边壁区湍流动量相平衡,且ti+2时刻运动沙粒群动量超过ti+1时刻,说明在湍流的作用下,有部分沙粒直接被湍流卷吸而进入跃移层。

ti+3时刻边壁区的下扫事件结束,主流区和边壁区湍流进入相对平静的随机脉动阶段,风沙两相流仍处于失衡状态(运动沙粒群仍处于高动量状态,而主流区和边壁区湍流动量已经衰减),这时风沙两相流动量分配的关系为:

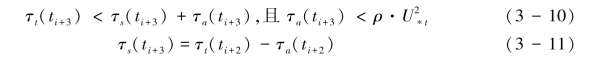
ti+4时刻无论湍流脉动状况如何,但这时主流区和边壁区湍流动量必然低于湍流结构的形成阶段,这时τs(ti+4)＆lt;τs(ti+3)并重新建立起气固两相流的平衡,具有如式(3-5)的动量分配关系。式(3-5)~式(3-11)说明受湍流相干结构演化的驱动,跃移系统的自平衡演化过程。相似地,湍流随机脉动也能导致类似的跃移系统自平衡调整模式,所不同的是,湍流切应力超过ρ·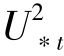的事件呈现无组织状态,缺乏过程上的连续性。不仅湍流动量变化会驱动跃移系统的演化,沙粒群碰撞过程动量的损失也会引起跃移系统从平衡-不平衡-平衡状态的演化,这主要是因为沙粒之间的空中碰撞、沙粒-床面之间随机的非弹性碰撞所导致的运动沙粒群的萎缩。Rumple认为在入射颗粒与床面碰撞过程中(Rumple,1985),只有每个高速反弹颗粒垂直速度大于撞击垂直速度,高能反弹颗粒损失的垂直动量才得以恢复和连续跃移才能够维持,但这需要满足颗粒撞击角小于15°条件。受床面粒度分布、颗粒形状等因素影响,部分沙粒的实际撞击角会超过这个范围(Zhang, et al., 2007),这意味着部分颗粒在碰撞过程中由于垂直动量损失而退出跃移系统,跃移输送存在萎缩趋势。纯高速钢珠碰撞实验表明,在几乎完全弹性碰撞情况下,仍有6%的颗粒不再反弹或丧失高能反弹的特征,且在这些高能反弹颗粒的垂直动量仅有撞击颗粒的34%~72% (Mitha, et al., 1986),这说明纯粹颗粒-床碰撞过程必然是衰减的。Willetts ＆amp; Rice(1986)风洞实验表明,在粒-床碰撞过程中,粗、中、细等三类石英沙的垂直动量恢复系数小于1的概率分别为57%,48%,29%。Rice et al.(1995) 发现,在颗粒-床中碰撞颗粒水平动量26%~44%的损失在床面(其中一部分可能转换成蠕移颗粒的动量)。风洞实验观测(Dong, et al., 2002, 2004)和数值模拟(Sørensen ＆amp; McEwan, 1996;Dong, et al., 2005; Huang, et al., 2007)均表明在较高风速情况下存在明显的空中碰撞,而空中碰撞增加了粒-床碰撞的动量损失并减少了起跳沙粒数目而起到调节跃移系统作用(Wang, et al., 2008)。前人认为碰撞颗粒在下降阶段比上升阶段空中碰撞概率更大(Dong, et al., 2004),这将显著地增大颗粒群的撞击角,而按照前人的理论分析(Rumple, 1985),撞击角大于15°则造成部分高能反弹颗粒在碰撞过程中垂直动量损失而退出跃移系统。风沙流实验表明,约有10%~30%的跃移颗粒动量恢复系数小于1(Wang, et al., 2008),说明跃移输送过程中垂直动量亏损很显著。由此可以分析,碰撞过程的动量损失可导致运动沙粒群的萎缩并使气固两相流失衡,会出现式(3-5)中的τs(z)衰减而导致跃移系统的自我调整以维持气固两相流的平衡。

总之,在湍流相干结构、湍流随机脉动和运动沙粒群动量亏损等因素的共同作用下,风沙两相流总是处于动态演化过程。

风沙两相流动态演化过程必将伴随着沙粒起跳动力学的交替变化,形成冲击起动-普通空气动力学起动-猝发起动等起动方式交替变化的模式。当风沙两相流达到平衡时,沙粒起跳为典型的冲击起动方式;当气固两相流失衡时,沙粒起跳存在以下方式:以冲击起动为主和普通空气动力学起动为辅、以普通空气动力学起动为主、空气动力学猝发起动等,这几种起动方式可以用主流区和边壁区湍流状态、起跳沙粒群动量和沙粒群碰撞过程的动量损失等指标来定义和说明。

据式(3-6),ti时刻风沙两相流达到平衡状态,沙粒起跳可看作是典型冲击起动,设撞击颗粒群中粒径为ds颗粒的质量、水平速度和垂直速度分别m(ds),u(ds),v(ds),则撞击沙粒群的水平动量Mh(ti)和垂直动量Mv(ti)分别为式(3-12)和式(3-13),起跳沙粒粒径为dsl颗粒的质量、水平速度和垂直速度分别m(dsl),u′(dsl),v′(dsl),相应的水平动量M′h(ti)和垂直动量M′v(ti)分别为式(3-14)和式(3-15),令沙粒群碰撞过程水平动量损失ΔMh(ti)和垂直动量损失ΔMv(ti)分别为式(3-16)和式(3-17)。设风沙两相流输运的动态演化时间T内,所有典型冲击起动阶段对应的平均水平动量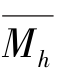和垂直动量损失Mv分别为式(3-18)和式(3-19),其中Λ为时间T内纯粹冲击起动事件的次数。

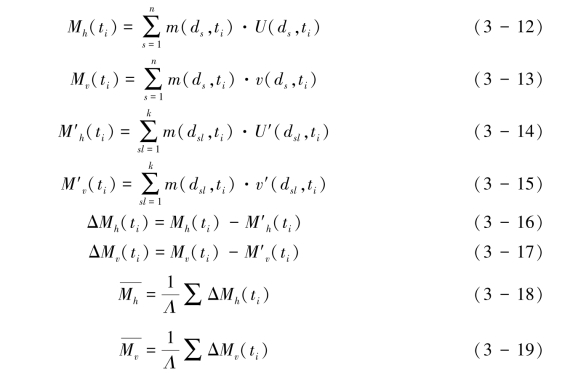
当ti+1时刻及之后的ti+2和ti+3时刻,边壁区动量满足τa(ti+1)＆g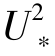t;ρ·t,且边壁区动量增加为湍流上抛、下扫等事件的生成所引起,相应地气固两相流由失衡向平衡演化过程中(见式(3-10)~式(3-11)),则可以认为ti+2和ti+3时刻沙粒起跳可看作是典型的湍流卷吸所导致的空气动力学猝发起动。风沙科学研究人员把湍流猝发所引起沙粒起动称作猝发起动。著者认为风沙颗粒的猝发起动具有三方面的特征:①起跳沙粒群的起跳速度、角度与上抛、下扫等湍流结构相对应;②猝发起动的沙粒群之间碰撞的概率小,运动沙粒群碰撞的水平动量损失ΔMhc(ti+2),ΔMhc(ti+3)和垂直动量损失ΔMvc(ti+2),ΔMvc(ti+3)远比典型冲击起动的动量损失小。同样地,在风沙两相流输运的观测时间T内,所有猝发起动过程中对应的平均水平动量损失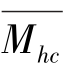和垂直动量损失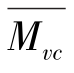也远比典型冲击起动的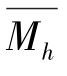和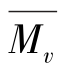小;③猝发起动与湍流相干结构形成过程中所伴生的流向湍涡卷吸相联系。和其他起动方式相比较,猝发起动具有很强的阵发性,可看成是湍流动量急剧释放所导致大量沙粒群的起跳。

若tp时刻边壁区动量满足τa(tp)＆g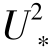t;ρ·t,且边壁区动量增加随机脉动所引起,则tp+1时刻必然会有部分沙粒被气流直接拖曳而起跳,同时有部分沙粒被其他沙粒冲击而起跳,而整个起跳的沙粒群究竟是以普通的空气动力学起动为主还是以冲击起动为主,需要利用沙粒群碰撞过程的动量损失来区分。这里把tp+1沙粒群的水平动量损失ΔMh(tp+1)和垂直动量损失ΔMv(tp+1)与典型冲击起动和空气动力学猝发起动对应的平均动量损失做比较,会存在式(3-20)和式(3-21)的关系。若ΔMh(tp+1)和ΔMv(tp+1)满足式(3-22),则定义沙粒起动以冲击起动为主;若满足式(3-23),则定义沙粒起动以普通空气动力学起动为主;若满足式(3-24),则定义沙粒起动普通空气动力学起动+冲击起动。

著者认为,湍流随机脉动导致的普通空气动力学的起动无论是在湍流释放动量强度、还是在风沙颗粒起跳的阵发性以及沙粒群碰撞过程的动量损失等方面都与湍流相干结构产生的空气动力学猝发起动存在明显的区别,因而这里把空气动力学起动划分为普通空气动力学起动和空气动力学的猝发起动。

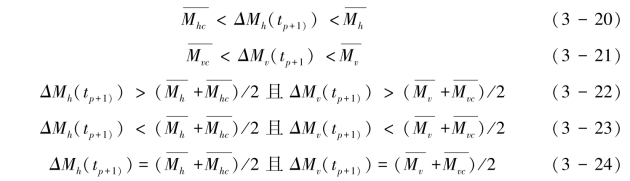
综上所述,借助于湍流解析和起跳沙粒群的动量损失状况可以把风沙颗粒起动方式界定为以下4种类型(见图3-7)。随着湍流状态的变化、运动沙粒群碰撞过程中动量损失的调整,风沙两相流始终处于平衡-不平衡-平衡的动态演化过程,沙粒群的起跳也出现相应地调整,由风沙两相流平衡状态的典型冲击起动演化为非平衡状态的以冲击起动为主、普通空气动力学起动为主、空气动力学猝发起动等起动方式,这些起动方式交替出现在风沙两相流输运过程之中,推动着风沙流的动态演化。未来需要搞清楚的问题是,在整个风沙两相流动过程中,沙粒的空气动力学猝发起动与普通空气动力学起动、冲击等起动方式在气固两相流的动量输运特征、沙粒起跳速度分布特征等方面的差异以及它们之间的主次关系,才可能深入地揭示风沙颗粒起跳的动力学机制。

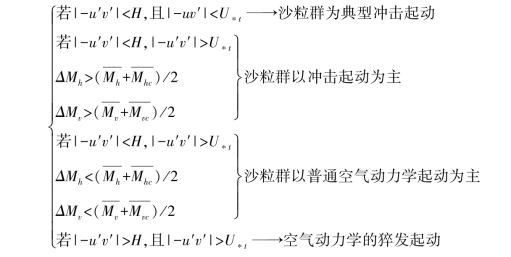
图3-7　风沙颗粒起动的概念模式

-u′v′是边壁区动量输运量,H为判断湍流相干结构与湍流随机脉动的阈值,ΔMh和ΔMv为任意时刻运动沙粒群碰撞导致的水平动量损失和垂直动量损失,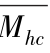与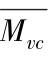分别是指在时间T内,空气动力学猝发起动对应的运动沙粒群碰撞导致的平均水平动量损失和垂直动量损失,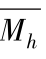和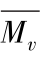为典型冲击起动对应的运动沙粒群碰撞导致的平均水平动量损失和垂直动量损失(梅凡民, 2011)。