1.4.2 半经验模型评述
和统计模型相比较,半经验模型的优点是能够定量地展现雨滴溅蚀过程的物理机理如雨滴动量传递与土壤颗粒溅射的关系等。Furbish et al(2007)模式模拟了单个雨滴动量在下坡向分配、单雨滴动量分配与溅射距离的关系,其在数学处理上是巧妙的。尽管关于土壤颗粒溅射距离的观测结果来自单一沙粒,但从溅射距离径向分布趋势来看(e.g.Van Dijk, et al., 2002; Legout, et al., 2005;Legue′dois, et al., 2005),溅射距离的负指数分布趋势可以从松散的沙质土壤扩展到黏质土壤,因而建模机理是基本可靠的(实际上负指数分布是近似的而非准确的表述,见Dijk, et al., 2002)。
式(1-18)被称为半经验模式,是因为ΨΧ的推导和计算涉及了很多的假定和经验性的观测数据,因而该模式有一定的局限性,其不确定性包括了γ、Ψ0、ξ′、Ns等参数估计带来的误差。另外,建模所依据实验结果是在单一粒径的沙粒、单一粒径的雨滴等极为简化和理想的实验条件取得的,因而模式的普适性受到质疑(Dunne, et al., 2009)。
更重要的是,研究者未充分讨论经验参数的估计方法,从而限制了模型应用。在建模的过程中,Furbish et al(2007)用高速摄影观测了3类均匀沙粒的溅射过程和轨迹,这为确定Ψ0提供了方法,但从应用的角度来看,发展更一般的估计Ψ0方法显然很有必要,其他参数估计也应如此,如参数Ns的估计。Furbish et al(2007)的文章中没有明确交代Ns的估计依据和方法。
除前人研究的一些结果可参考外(e.g., McCarthy, 1980; Mouzai & Bouhadef,2003),本书著者推荐利用式(1-9)或式(1-10),并借助数学推导获得单个雨滴溅射的颗粒数或质量等参数式(1-9)和式(1-10)出现在Furbish et al(2007)论文的附录之中,主要是为了宏观地解释单雨滴动量和溅蚀颗粒起跳之间的定量关系,并没有明确地推荐用来估计单个雨滴溅蚀的颗粒数或质量的方法。对式(1-9)而言,若雨滴撞击床面的粒径分布参数和堆积结构参数如孔隙率和容重可知,数值方法能提供雨滴撞击颗粒的数量、质量和速度(这里涉及雨滴-土壤颗粒的碰撞及土壤颗粒之间的碰撞),且数值方法所得结果更有普适性。另外,从Furbish et al(2007)溅蚀观测结果来看,溅蚀颗粒分为2类,一类是在雨滴碰撞、变形、恢复等过程直接溅射的颗粒,这类颗粒具有较高的速度和更长跃距,是液固碰撞的结果;另一类是被雨滴击打的颗粒与床面静止颗粒碰撞后溅射的颗粒,其具有低速度、短跃距或蠕移(基于高速摄影对风沙颗粒运动的观测,本书著者发现,前人讨论的蠕移可能被高估,几乎大部分床面附近沙粒都是跃移的,只不过起跳速度和跃距较小)。从溅射距离的负指数分布趋势来看(e.g.Van Dijk et al., 2002; Legout, et al., 2005;Legue′dois, et al., 2005;Furbish, et al., 2007),后者占比更高,据此可以统计前人观测的溅射颗粒速度或溅射距离来估计单雨滴溅蚀颗粒的平均速度,从而据式(1-9)计算单雨滴溅蚀土壤颗粒的质量和数目。和数值方法相比较,后一种方法更易实现。
式(1-10)为进一步估计单雨滴溅蚀颗粒的质量和数目提供了思路。式(1-10)预示着溅蚀颗粒的质量与平均溅蚀距离的乘积与单雨滴动量成正比。该式可变形为溅蚀质量的函数,而式(1-18)包含下坡向平均溅射距离等参数,则可以把式(1-10)代入式(1-18),这样就可以消去ΨX,但这里需要估计公式中所涉及的经验参数。另外,建立单雨滴溅蚀颗粒质量和数目模式时,应该考虑不同粒径雨滴的差异,因为实际降雨事件中有特定的雨滴谱,而小雨滴可能对颗粒溅蚀是无效的(e.g.Ekern & Muckenhirn, 1947; McCarthy, 1980)。
总之,期望半经验模型能够应用于具体土壤溅蚀场景,需要建立普适性经验参数的估计方法和数据库。通过对前人的观测数据分类、统计,有望建立普适性经验参数的估计方法。
基于相似建模思路,Dunne et al.(2009)发展了Furbish et al.(2007)模式以便能够预测植被覆盖、多粒径分布的松散和黏结土壤的坡地溅蚀输送强度。在建模的方法上,Dunne et al.(2009)作了以下几个方面的改进:
1)引入下坡向溅蚀质量比率/分数η(Fraction of sediment splashed downslope)来表征单个雨滴溅蚀强度随坡度和坡向的变化趋势及雨滴动量在上坡向和下坡向的分布。和具有相同功能的式(1-6)、式(1-11)和式(1-12)等理论公式相比较,下坡向溅蚀质量比率/分数η是基于室内实验观测的统计公式,其可以表示为式(1-19)和式(1-20):其中式(1-20)适合表述坡度在25°(0.44弧度)以下的情形。式(1-19)和式(1-20)的优点是简洁的,不需复杂的计算,但应该看到该统计模式仅是对沙粒溅蚀结果的归纳,其普适性还需要进一步验证。
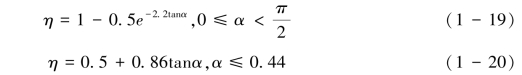
2)利用牛顿第二定律计算平均径向溅射距离r,其可以表征为平均起跳角β和平均起跳速度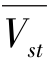 及径向方位角θ的函数,见式(1-21):但用式(1-6)、式(1-11)和式(1-12)来推测平均溅射距离更简洁。
及径向方位角θ的函数,见式(1-21):但用式(1-6)、式(1-11)和式(1-12)来推测平均溅射距离更简洁。
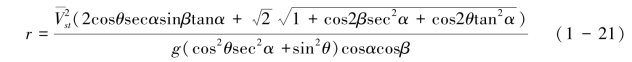 (https://www.daowen.com)
(https://www.daowen.com)
3)借助Reeve(1982)上坡向和下坡向溅蚀输送率模式建立净溅蚀率积分式,即式(1-22)~式(1-24),它们分别代表上坡向、下坡向和净溅蚀单位宽度输送率。
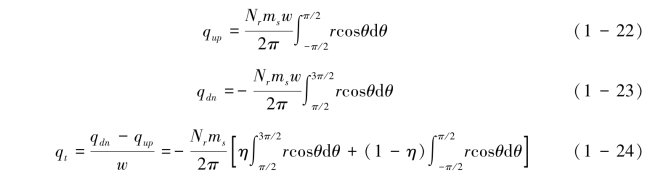
4)对式(1-24)进行参数化处理:根据前人实验室实测数据,令β=11°,α=0,η=0.5可求得平面上平均溅蚀率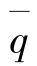 的解析式(1-25):
的解析式(1-25):
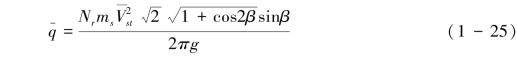
基于非洲草原野外实验观测的平均溅蚀率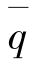 的统计模式为式(1-26):这里a=0.0104, b=-10.28, j=0.927, C代表植被覆盖度。式(1-26)的优点是综合考虑了植被覆盖度和多种土壤类型对平坦床面平均溅蚀输送强度的影响,这使得新发展模式有更广泛的应用场景。
的统计模式为式(1-26):这里a=0.0104, b=-10.28, j=0.927, C代表植被覆盖度。式(1-26)的优点是综合考虑了植被覆盖度和多种土壤类型对平坦床面平均溅蚀输送强度的影响,这使得新发展模式有更广泛的应用场景。

联立式(1-25)和式(1-26)得到关于Nrms的表达式,将其代入式(1-24)就可以得到qt的新函数式(1-27):
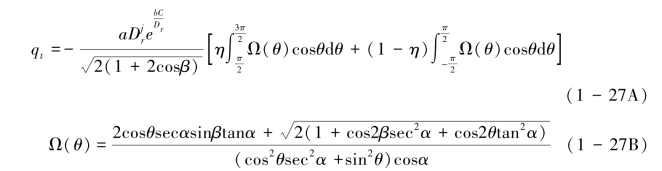
式(1-27)巧妙地消去待定参数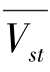 ,从而规避了估计
,从而规避了估计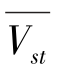 带来的误差。同时式(1-27)可以预测植被覆盖条件下瞬时溅蚀输送通量,其具有更广泛的应用范围。
带来的误差。同时式(1-27)可以预测植被覆盖条件下瞬时溅蚀输送通量,其具有更广泛的应用范围。
总之,基于单雨滴碰撞行为的半经验模型是涵盖了溅蚀的主要机理,它们比纯粹的统计模式有更好的普适性。但是,模式包含的经验参数常常是推测的或者来自有限的观测数据,如Furbish et al.(2007)模式关于平均溅射距离的推测、Dunne et al.(2009)模式中关于平均溅射角(起跳角)的推测、单雨滴溅蚀颗粒质量等参数的推测等。这些经验参数的估计误差给半经验模型的预测结果还存在不确定性。实际上,这些经验参数常和未知的物理机理联系在一起,借助数值算法和提高实验观测水平是提高经验参数估计精度的有效途径。特别是,数值方法能模拟雨滴-颗粒、颗粒-颗粒之间的多颗粒碰撞过程,其能从微观上揭示雨滴溅蚀过程和确定溅蚀过程的经验参数。
