4.4.1 总体研究状况分析
粒-床碰撞是风沙输运的关键环节,因而从逻辑上说,改进粒-床碰撞的观测与模拟工作对完善跃移输送的研究有着重要意义。同时,粒-床碰撞过程还是沙波纹形成和演化的主导因素,理解粒-床碰撞的机理对认识风成沙波纹演化机理有重要作用。粒-床碰撞现象也是颗粒物理学、能源、化工、制药等领域共同关注的科学问题,揭示其机理对相关领域和学科也有重要的借鉴价值。
粒-床碰撞的观测研究主要通过高速摄影技术来追踪沙粒的轨迹,并进而根据运动沙粒群的时空关系来分析、鉴别入射-反弹和溅射颗粒。通过提取运动轨迹和运动参数以统计模式如溅射函数来揭示粒-床碰撞规律(e.g.Willetts ＆amp; Rice, 1986, 1989; White ＆amp;Schulz, 1977; Nalpanis, et al., 1993; Rice, et al., 1996; Zou, et al., 2001; Beladjine, et al, 2007; Zhang, et al., 2007; Oger, et al., 2008; Wang, et al., 2008; Yang, et al.,2013; Pokorny ＆amp; Horender, 2014; O'Brien ＆amp;Neuman, 2016, 2017)。此外,亦可利用激光多普勒测速技术和粒子图像测速技术通过测定风沙颗粒群的速度分布及建立的起跳速度的概率分布模式来间接地反映粒-床碰撞规律(e.g.Dong, et al., 2002a, 2004; Kang, et al., 2007; Rasmussen ＆amp; Sørensen, 2008; Li ＆amp; Neuman, 2012; Ho ＆amp; Dupont, 2013),相比较而言,高建摄影方法所获信息更为全面。
目前用于模拟粒-床碰撞的计算方法有2类。一类是基于经典动量定理的解析模式或称为硬球模式(即忽略碰撞接触面上局部弹塑性变形细节)。按照封闭动量方程组而引入的假设条件的差异,该类模型可分为3种方案,分别为Wang ＆amp; Mason (1992)方案、Walton ＆amp; Braun (1986)方案、Crowe et al(1998)方案等。硬球模型仅适合处理两颗粒的碰撞,前人经过对其巧妙处理来模拟多颗粒的粒-床碰撞过程(Sun, et al., 2001; Zheng, et al., 2006; Crassous, et al., 2007)。另一类计算方法是数值算法,它也被称为离散元模型或软球模型(考虑碰撞界面上的变形过程),这类算法可分为基于接触力学的Hertz-Mindlin-Deresiewicz(1953)模型或简化模型(孙其成和王光谦, 2009)、以及基于弹簧振子假定的Cundall ＆amp; Strack (1979)模型。和弹簧振子模型相比较,基于接触力学的离散模型的计算过程更复杂。这两类数值模型分别被用来模拟粒-床碰撞过程及沙粒起跳速度的概率分布特征(e.g.Wener, 1988, 1990; Anderson ＆amp; Haff, 1991; Kang, et al., 2010; Yang, et al., 2010; Kang ＆amp; Zou, 2011; Xiao, et al., 2012; Kang, 2013; Duan, et al., 2013; Xing＆amp; He, 2013; Huang, et al., 2017; Tanabe, et al., 2017; Yin, et al., 2017)。
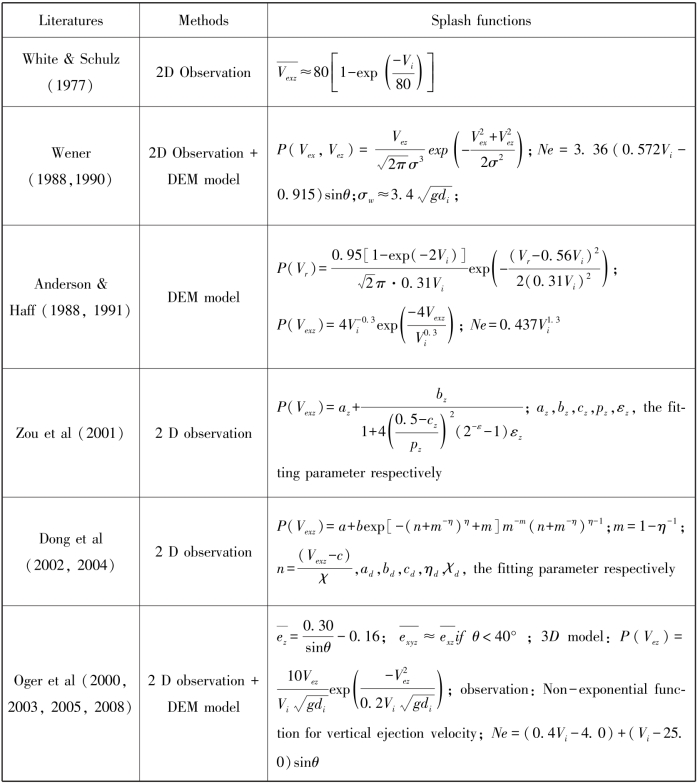
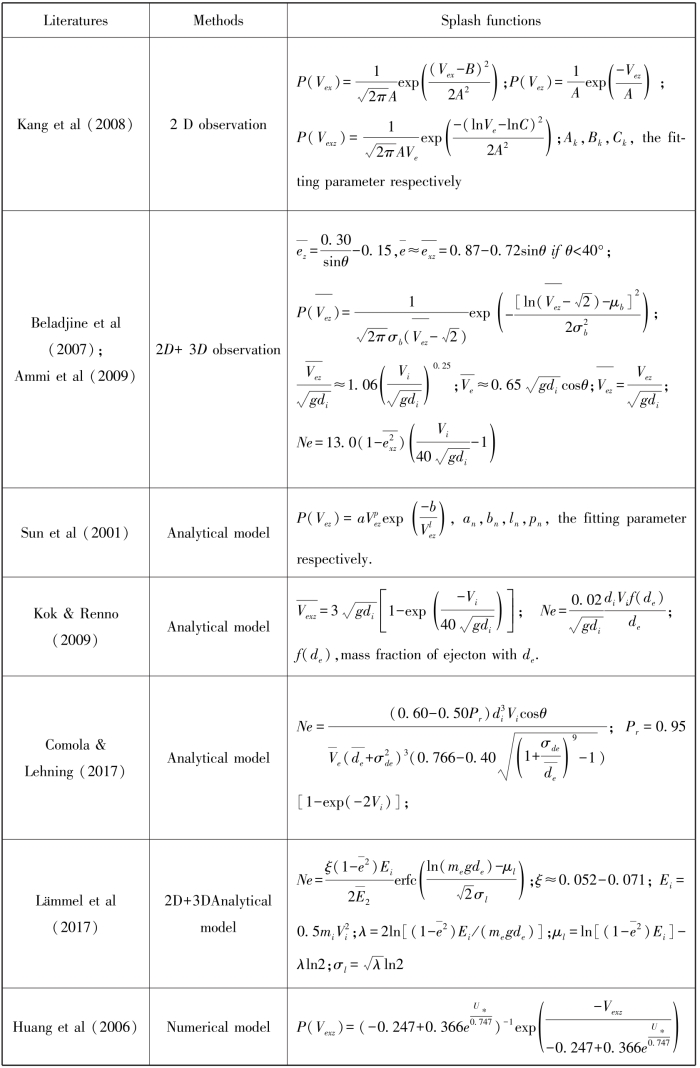
表4-7显示了通过实验观测、理论模拟和数值模拟等方法获得的溅射函数。完整的溅射函数是用入射速度、入射角度、床面参数来预测粒-床碰撞后反弹速度、反弹速度概率分布、平均的溅射速度、溅射速度概率分布、溅射颗粒数等(Anderson ＆amp; Haff, 1988)。定性地看,这些溅射函数展示了一些共同规律:反弹速度与入射速度比值随入射角增大而减小;溅射颗粒数随着入射速度增加而增加。然而,定量地看,这些溅射函数在以下3个方面还存在着明显差异:①溅射垂直速度与入射速度关系上的差异:溅射垂直速度分别被认为与入射速度无关(Werner, 1990)、为入射速度的幂函数(Beladjine, et al., 2007; Ammi,et al., 2009; Anderson ＆amp; Haff, 1991)、为入射速度的线性函数(Oger, et al., 2005, 2008;Xing, ＆amp; He, 2013;)、碰撞早期受入射速度制约而后期与入射速度无关(Tanabe, et al.,2017);②溅射速度概率分布函数的差异:溅射垂直速度的概率分布分别服从Gamma函数(Anderson ＆amp; Hallet, 1986; Zhou, et al., 2006)、负指数函数(Xing ＆amp; Guo, 2004; Kang, et al., 2008)、Rayleigh分布(Oger, et al., 2005, 2008)、对数正态分布函数(Beladjine, et al., 2007;Ammi, et al., 2009;Ho, et al., 2012)、正态分布函数(Yang, et al., 2010)、麦克斯韦分布函数(Sun, et al., 2001)等。溅射的水平速度分布分别服从正态分布(Kang,et al., 2008)、对数正态分布(Yang, et al., 2010);溅射合速度(二维尺度上)分别服从负指数分布(Anderson ＆amp;Haff, 1988, 1991; Huang, et al., 2006)、Pearson VII分布(Zou, et al., 2001)、韦布尔分布(Dong, et al., 2002a)、对数正态分布(Kang,et al.,2008; Xing ＆amp;He, 2013; Yin, et al., 2017)等;③溅射颗粒数函数之间的差异:溅射颗粒数分别为入射速度和入射角正弦值的线性函数(Oger, et al., 2005, 2008; Yin, et al., 2017)、入射速度的幂函数(Anderson ＆amp; Haff, 1991; Andreotti, 2004)、有效恢复系数和入射速度的复合函数(Beladjine, et al., 2007; Ammi, et al., 2009)、粒径分布和入射速度的复合函数(Kok＆amp; Renno, 2009; Comola ＆amp; Lehning, 2017)、入射动能、粒径、有效恢复系数及溅射沙粒动能分布误差函数的复合函数(Lämmel, et al., 2017)、入射速度、入射角及入射沙粒与床面粒径比的负指数的复合函数(Huang, et al., 2017)。这些形式多样的溅射函数的成因目前还缺乏系统的理论解释,仅有的研究是用级联碰撞模式来解释溅射速度的对数正态分布的原因(Ho, et al., 2012)。相应地,造成溅射函数差异的原因也不清楚。
著者认为,造成前述溅射函数显著差异的原因可能有:①实验观测手段如高速摄影测速与激光多普勒效应测速的差异,前者利用轨迹追踪算法间接测速而后者利用激光干涉条纹宽度直接测速,后者测速精度应高于前者,前者涉及风沙颗粒轨迹追踪算法的发展问题,见后面论述;②模拟计算在初始条件、模型原理和精度的差异。具体模型的差异见后面论述。
表4-7 部分溅射函数的比较(Vi-impact velocity,θ-incidentangular, Vr-rebound velocity, Vex, Vey,Vez, Vexz, Vexyz-horizontal, lateral, vertical,resultant vecolcity in 2D, 3D of ejecton respectively, ez, exyz-effective restitution coefficient of vertical velocity, resultant velocity respectively, Ne-the number of ejections, P(variable)-probability of the variable, me-mass of a ejected particle, di, de-diameter of incident and ejected particle, the bar of variable-average value, U∗-wind friction velocity)
续表
续表
