2.1.2 基带数据信号的功率谱特性
要把基带数据信号传送出去,研究其频谱特性是非常重要的。由于数据序列是随机的,基带数据信号是随机信号,这样就不能用分析确定信号的方法来分析其频谱,只能用随机信号的分析理论,研究它的功率谱密度。
1.基带数据信号的一般表示式
图2-1给出的基带数据信号的单个码元波形都是矩形的,但实际上并非一定是矩形。为不失一般性,我们令g 1(t)代表二进制数据符号的“0”,g 2(t)代表“1”,码元间隔为T s。假设数据序列出现“0”和“1”概率分别为P和1-P,且认为它们的出现是统计独立的,则基带数据信号可表示为
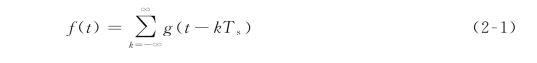
其中:
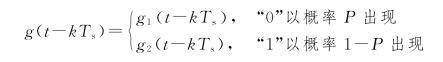
如果一个数据信号序列为101101,可以用单极性矩形脉冲序列来表示,令g 1(t)=0,g 2(t)是宽度为T s的矩形脉冲,如图2-2所示。同理,也可以画出其他形式的波形图来,但是很显然g 1(t)≠g 2(t)。

图2-2 单极性不归零矩形脉冲序列示意图
2.基带数据信号的功率谱密度
(1)基本分析利用随机信号的分析方法,得到式(2-1)所示基带数据信号的功率谱密度为

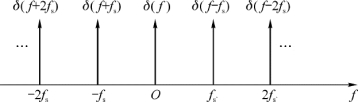
图2-3 频域上的单位冲激序列
从式(2-2)可看出,随机基带数据信号的功率谱密度可能包括两个部分:连续谱p u(f)和离散谱p v(f)。因为表示数据码元的g 1(t)和g 2(t)是不能完全相同的,则其对应的傅里叶变换G 1(f)≠G 2(f),所以连续谱部分总是存在的。而离散谱是否存在,则与信号码元出现“1”,“0”的概率以及码元的波形有关,在某些情况下可能没有离散谱分量。
例如,当P=1/2,G 1(f)=-G 2(f)=G(f)时,式(2-2)变为
![]()
这时功率谱密度中没有离散谱分量。
(2)几种基带数据信号的功率谱密度
下面来求以矩形脉冲为单个码元波形的几种基带数据信号的功率谱密度。首先,单个矩形脉冲可以表示为

其傅里叶变换为
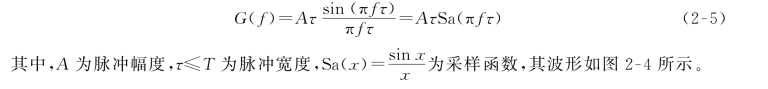 (https://www.daowen.com)
(https://www.daowen.com)
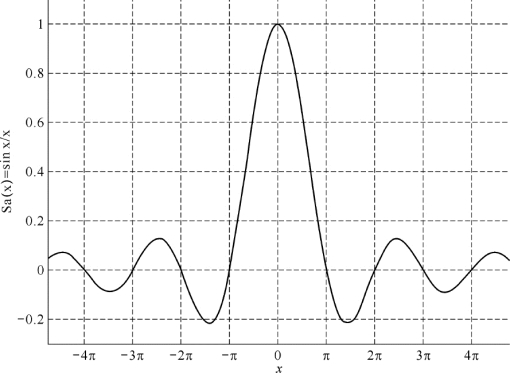
图2-4 采样函数波形
为了分析简便,我们假设“1”和“0”出现的概率相等,即P=1/2。
①单极性归零信号
设“0”码为g 1(t)=0,“1”码为脉冲宽度为τ的矩形脉冲,即g 2(t)=g(t),其中τ<T s。则由式(2-2)得其功率谱密度为
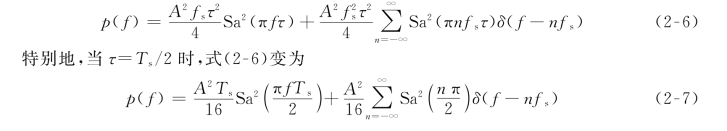
②单极性不归零信号
设“0”码为g 1(t)=0,“1”码为脉冲宽度为T s的矩形脉冲。即g 2(t)=g(t),其中τ=T s。则直接由式(2-6),得其功率谱密度为
![]()
③双极性归零信号
设“0”码和“1”码分别是脉冲宽度为τ、幅度为±A的矩形脉冲。即g 1(t)=-g 2(t)=g(t),其中τ<T s,此时G 1(f)=G 2(f)。则由式(2-2)得其功率谱密度为
![]()
特别地,当τ=T s/2时,式(2-9)变为

④双极性不归零序列
设“0”码和“1”码分别是脉冲宽度为T s、幅度为±A的矩形脉冲,则由式(2-9),令τ=T s可得其功率谱密度为
![]()
为了便于对比,将式(2-7)、式(2-8)、式(2-10)和式(2-11)所示功率谱密度用图2-5表示。
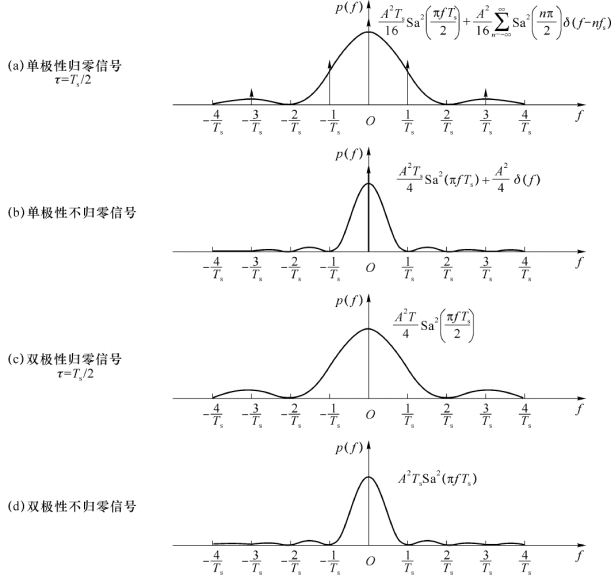
图2-5 四种基带数据信号的功率谱密度
由以上功率谱分析及图2-5可以看出:P=1/2时,对于g 1(t)=-g 2(t)=g(t)这样的双极性信号是不含有离散谱分量的;而单极性信号含离散谱分量,且离散谱分量的特征与单个码元的波形有关。
分析基带数据信号的功率谱密度是很有意义的。其一,离散谱是否存在决定了我们能否直接从基带数据信号中提取定时信息,或者如何才能提取定时信息,这对数据传输系统是非常重要的。其二,通过图2-5中对四种信号的对比分析发现,脉冲宽度越宽,其能量集中的范围就越小;脉冲宽度越窄,其能量集中的范围就越大。(由此可大概了解传输这种数据信号所需要的基带宽度。)
