3.5.2 卷积码的图解表示
根据卷积码的特点,它还可以用树状图、网格图和状态图来表示,它与卷积码的编码过程和解码方法有密切关系。
1.树状图
下面我们对图3-14所示的(2,1,3)卷积码编码器进行讨论。与一般形式相比,输出移位寄存器用转换开关代替,转换开关每输入一个比特转换一次,这样,每输入一个比特,经编码器产生两个比特。图3-14中m 1,m 2,m 3为移位寄存器,假设移位寄存器的起始状态全为“0”,即m 1,m 2,m 3为000。c 1与c 2表示为m 1表示当前的输入比特,而移位寄存器m 3,m 2存储以前的信息,表示编码器状态。

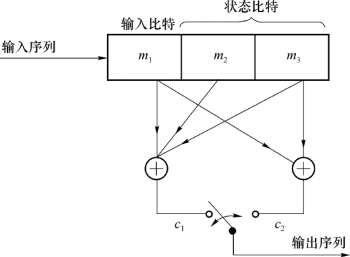
图3-14 (2,1,3)卷积码编码器
为了说明编码器的状态,表3-10列出了它的状态变化过程:第1个输入比特为“1”,这时m 1=1,因为m 3m 2=00,所以输出码元c 1c 2=11;第2个输入比特为“1”,这时m 1=1,m 3m 2=01,c 1c 2=01;依此类推,为保证输入的全部信息位11010都能通过移位寄存器,还必须在输入信息位后加3个“0”。
表3-10 (2,1,3)卷积码编码器的状态变化过程

编码器中移位过程可能产生的各种序列可以用树状图来表示,如图3-15所示。
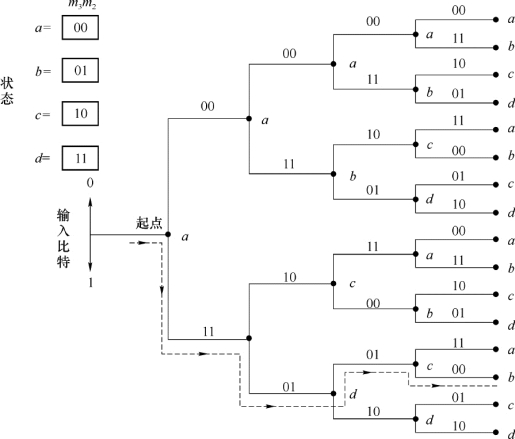
图3-15 (2,1,3)卷积码的树状图
图3-15中和表3-10中用a,b,c和d分别表示m 3m 2的4种可能状态,即a表示m 3m 2=00,b表示m 3m 2=01,c表示m 3m 2=10和d表示m 3m 2=11。树状图从节点a开始画,此时移位寄存器状态(即存储内容)为00。当输入第1个比特m 1=0时,输出比特c 1c 2=00;若m 1=1,则c 1c 2=11,因此,从a点出发有两条支路(树叉)可供选择,m 1=0时取上面一条支路,m 1=1则取下面一条支路。当输入第2个比特时,移位寄存器右移1位后,上支路情况下移位寄存器的状态仍为00,下支路的状态则为01,即b状态。再输入比特时,随着移位寄存器和输入比特的不同,树状图继续分叉成4条支路,2条向上,2条向下,上支路对应于输入比特为“0”,下支路对应于输入比特为“1”,如此继续下去,即可得到图3-15所示的树状图。
树状图上,每条树叉标注的码元为输出比特,每个节点上标注的a,b,c和d为移位器(m 3m 2)的状态。从该图可以看出,从第4条支路开始,树状图呈现出重复性,即图中标明的上半部与下半部完全相同。这表明从第4位输入比特开始,输出码元已与第1位输入比特无关,正说明(2,1,3)卷积码的约束长度为n N=2×3=6的含义。当输入序列为11010时,在树状图上用虚线标出了它的轨迹,并得到输出码元序列为11010100…,可见,该结果与表3-10一致。(https://www.daowen.com)
2.网格图
网格图又称格状图。卷积码的树状图中存在着重复性,据此可以得到更为紧凑的图形表示。在网格图中,把码树中具有相同的节点合并在一起,码树中的上支路对应于输入比特“0”,用实线表示;下支路对应于输入比特“1”,用虚线表示。网格图中支路上标注的码元为输出比特,自上而下4行节点分别表示a,b,c和d 4种状态,如图3-16所示。一般情况下,有2N-1种状态,从第N节(从左向右计数)开始,网格图图形开始重复而完全相同。
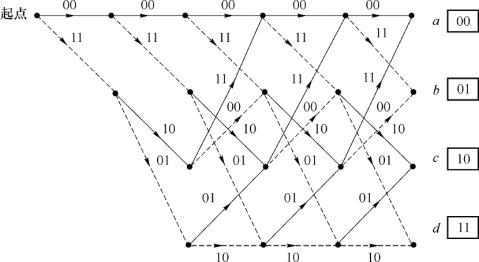
图3-16 (2,1,3)卷积码的网格图
3.状态图
从树状图3-15的第三级各节点状态a,b,c和d与第四级各节点a,b,c和d之间的关系,或者取出已达到稳定状态的一节网格(图3-16中第三级到第四级节点间的一节网格),我们就可将当前状态与下一个状态之间的关系用状态图来表示,如图3-17(a)所示。
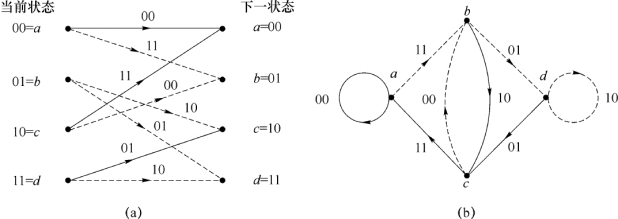
图3-17 (2,1,3)卷积码的状态图
图中实线表示输入比特为“0”的路径,虚线表示输入比特为“1”的路径,并在路径上写出了相应的输出码元,再把当前状态与下一个状态重叠起来,即可得到图3-17(b)所示的反映状态转移的状态图。在图(b)中有4个节点,即a,b,c和d,其对应取值与图(a)相同。每个节点有两条离开的弧线,实线表示输入比特为0,虚线表示输入比特为1,弧线旁的数字为输出码元。当输入比特序列为11010时,状态转移过程为a→b→d→c→b,相应输出码元序列为11010100…,与表3-10的结果相一致。注意,图(b)中两个自闭合圆环分别表示a→a和d→d状态转移。
由上述可见,当给定输入信息比特序列和起始状态时,可以用上述3种图解表示法的任何—种,找到输出序列和状态变化路径。
例3-7 图3-14所示卷积码,若起始状态为“0”,输入比特序列为110100,求输出序列的状态变化路径。
解 由卷积码的网格图3-16,找出编码时网格图中的路径如图3-18所示,由此可得到输出序列和状态变化路径,示于同一图中的上部。
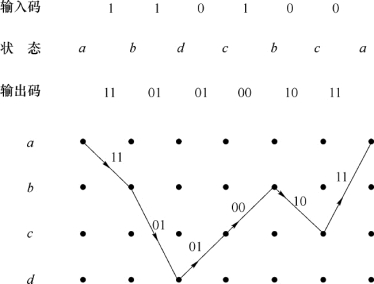
图3-18 (2,1,3)卷积码的编码过程和路径
