2.2.2　几种基带形成网络

2.2.2　几种基带形成网络

1.理想低通形成网络

首先分析一个理想化的情况来说明频带限制与传输速率之间的重要关系。假设图2-6中形成网络的系统传输特性是理想低通滤波型，如图2-7所示。其传递函数为

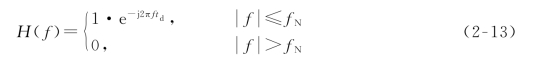
其中，f N为截止频率，t d为固定时延。其对于单位冲激脉冲δ(t)的响应，就是网络传递函数的傅里叶逆变换，即

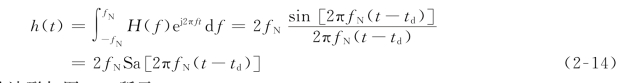
其t d=0时的波形如图2-8所示。

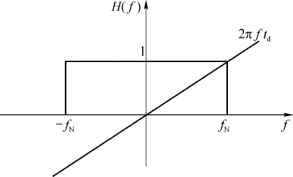
图2-7　理想低通传输特性

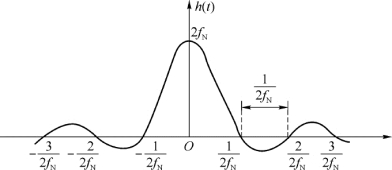
图2-8　理想低通的冲激响应

理想低通冲激响应波形的特点是:

·在t=t d处有最大值，在最大值两边作均匀间隔的衰减波动，以t=t d为中心每隔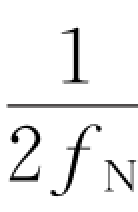出现一个过零点;

·波形“尾巴”以1/t的速度衰减。

如用式(2-12)表示的冲激脉冲序列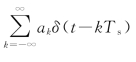加到理想低通网络的输入，即每隔码元间隔T s发送一个强度为a k的冲激脉冲，则按叠加定理，每个冲激脉冲在理想低通网络的输出都产生一个如图2-8的冲激响应a k·h(t)。因为h(t)在时域上是无限延伸的，所以这些冲激响应之间存在干扰，我们称这些干扰为码间干扰或符号间干扰。

特别地，如果选取系统的码元间隔T s=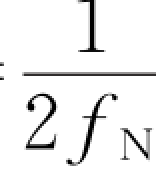，设输入的数据序列{a k}是101101，它通过理想低通网络形成的冲激响应序列如图2-9所示。由h(t)的波形特点可知，冲激响应序列的波形在峰值点上没有码间干扰(在其他点是有码间干扰的)。

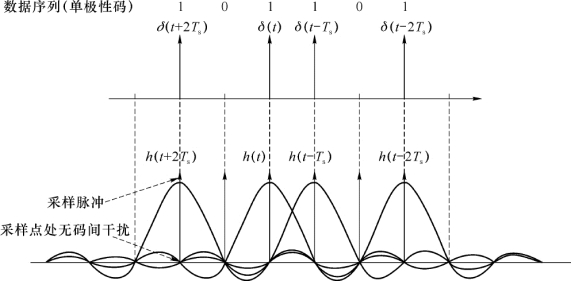
图2-9　冲激脉冲序列通过理想低通网络

此时，如果采样判决器按T s=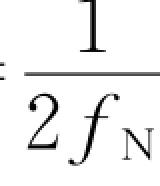进行采样，并且选取合适的采样时刻(图2-9画出了采样脉冲)，则可以准确地恢复传输的数据序列。由此得到接收波形满足采样值无失真传输的条件是:仅在本码元的采样时刻上有最大值，在其他码元的采样时刻为0(采样点无码间干扰)，而不要求整个波形无码间干扰。用公式来表示为

采样值无失真条件即奈奎斯特第一准则，该准则描述了码元传输速率与传输系统特性(对于理想低通形成网络主要是指截止频率f N)之间的关联关系。其详细表述是:若系统等效网络具有理想低通特性，且截止频率为f N，则该系统中允许的最高码元速率为2f N，这时系统输出波形在峰值点上不产生前后符号干扰。

由于该准则的重要性，国际上把f N称为奈奎斯特频带，2f N波特称为奈奎斯特速率，T s=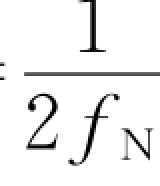称为奈奎斯特间隔。这一定理表明，在采样值无失真的条件下，在频带f N内，2f N波特是极限速率，即所有数字传输系统的最高频带利用率为2波特/赫兹(2 Baud/Hz)。

2.具有幅度滚降特性的低通形成网络

虽然理想低通形成网络能够达到频带利用率的极限——2 Baud/Hz，但是实际应用时存在两个问题。其一是，理想低通的传输特性是无法物理实现的。其二是，理想低通的冲激响应波形具有波动幅度很大的前导和后尾，对接收端定时精度要求很高(若采样时刻发生偏差，则会引入较大的码间干扰)。因此，要设计一个传输系统，它既可以物理实现，又能满足奈奎斯特第一准则的基本要求:速率为2f N的数据序列通过该系统后，能在所有间隔为T s=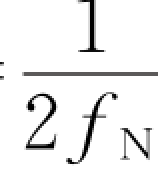的采样点处不产生码间干扰。理想低通形成网络之所以不可物理实现，在于它的幅频特性在截止频率f N处的垂直截止特性。可对理想低通特性的幅频特性加以修改，使它在f N处不是垂直截止而是有一定的滚降特性，如图2-10所示。这种滚降特性能满足奈奎斯特第一准则的条件是:滚降部分的波形关于点奇对称。

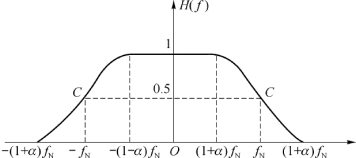
图2-10　幅频特性滚降的传输特性

滚降低通特性形成网络是可物理实现的，实际中一般采用具有升余弦频谱特性的形成网络，其传输特性可表示如下:

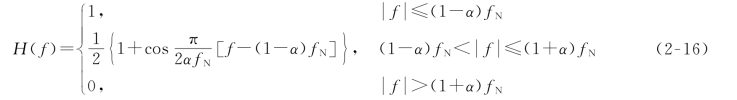
其中，α为滚降系数(0＜α≤1)，f N为对应理想低通幅频特性的截止频率，由于滚降而使网络的频带宽度增加了α·f N，则其所占频谱宽度为B=(1+α)f N。

升余弦低通形成网络的冲激响应h(t)为

其波形如图2-11所示。

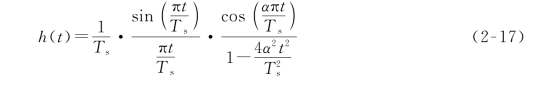
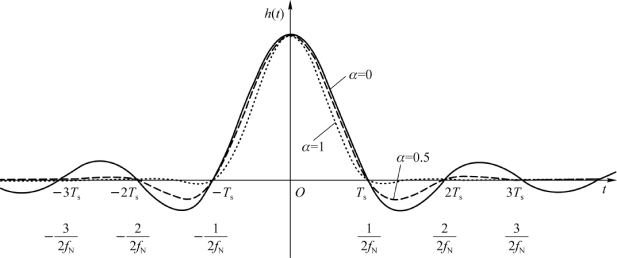
图2-11　升余弦幅频特性网络的冲激响应

从图中可以看到，h(t)波形在采样点(t=0)处达到最大值，在其他采样点上都为零，而且增加了一些新的零点。另外，升余弦特性相对理想低通特性而言，其h(t)波形的“尾巴”衰减比较快，因而对定时精度的要求较低。但是由于升余弦特性的频谱宽度有所增加，频带利用率(单位为Baud/Hz)就有所下降，表示为

例2-1 一形成滤波器幅度特性如图2-12所示，如果符合奈奎斯特第一准则，问:(a)其码元速率为多少?α为多少?(b)采用八电平传输时，数据传信速率为多少?(c)频带利用率η为多少Baud/Hz?

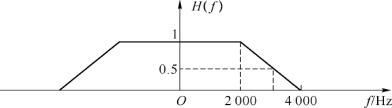
图2-12　例2-1图

解 (a)若符合奈奎斯特第一准则，则H(f)应以(f N，0.5)呈奇对称滚降，由图示可得:

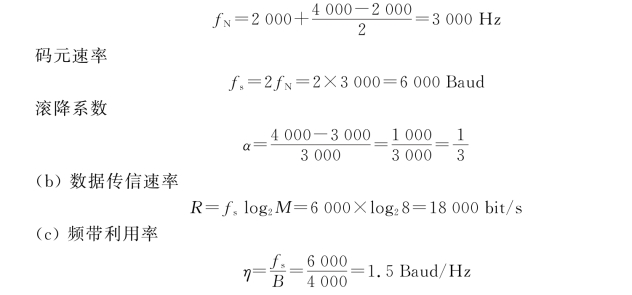
3.部分响应系统

(1)基本原理

根据奈奎斯特第一准则，上面设计了两类采样点无码间干扰的基带形成网络。其中，理想低通形成网络的特点是频谱窄，且频带利用率能够达到理论上的极限(2 Baud/Hz)，但缺点是波形“尾巴”衰减较慢，对定时要求比较严格，而且理想低通网络是无法物理实现的。虽然滚降低通形成网络的波形“尾巴”衰减较快，但是所需频带宽度增加了，从而使得频带利用率不能达到2 Baud/Hz的极限。那么能否找到一种形成网络，使其频带利用率能达到2 Baud/Hz的极限，而且冲激响应波形的“尾巴”衰减又较快?

奈奎斯特第二准则说明:有控制地在某些码元的采样时刻引入码间干扰，而在其余码元的采样时刻无码间干扰，就能使频带利用率达到理论上的最大值，同时又可降低对定时精度的要求。通常，把满足奈奎斯特第二准则的波形称为部分响应波形，采用部分响应波形的基带传输系统称为部分响应系统。

(2)第一类部分响应系统

部分响应系统的形成波形是两个或两个以上在时间错开的Sa(2πf Nt)所组成，例如第一类部分响应系统的合成波表达式为

此式在分母通分之后将出现t 2项，即波动衰减是随着t 2而增加，从而加快了响应波形的前导和后尾的衰减，其波形如图2-13所示。

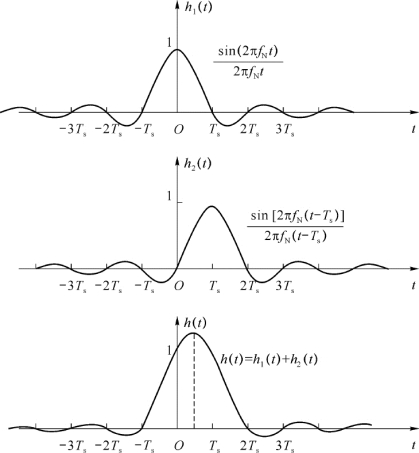
图2-13　第一类部分响应系统的形成波形

虽然合成波解决了Sa(2πf Nt)波形的定时精度的问题，但是它引入了相邻码元间的在采样时刻的干扰。例如，从图2-13中可以看出，假设按码元间隔T s发送和采样，h(t)波形在0与T s时刻都等于1(归一化值)，在其他k T s处为零，即存在码间干扰。但是可以看出，这种码间干扰是固定的，即如果已知前一码元发送的是“1”码，则对本码元采样时刻有一个固定为1的影响;若已知前一码元为“0”码，则对本码元无影响。所以这种有控的、固定的码间干扰，在收端是可以消除的。

下面仍以第一类部分响应系统为例，分析其幅频特性，如图2-14所示。

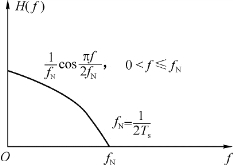
图2-14　第一类部分响应系统的幅频特性

其表达式为

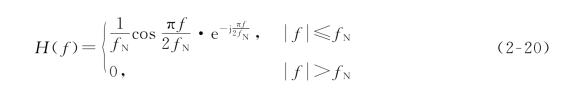
上述的H(f)特性称为余弦低通特性，从式(2-20)和图2-14可以看出系统占用频带宽度B=f N，则其频带利用率η=2f N/f N=2 Baud/Hz。

(3)部分响应系统的一般表示

常见的部分响应系统分别命名为第一、二、三、四和五类部分响应系统，如表2-1所示，其中应用最广的是第一类和第四类部分响应系统。

表2-1　几种常见的部分响应系统

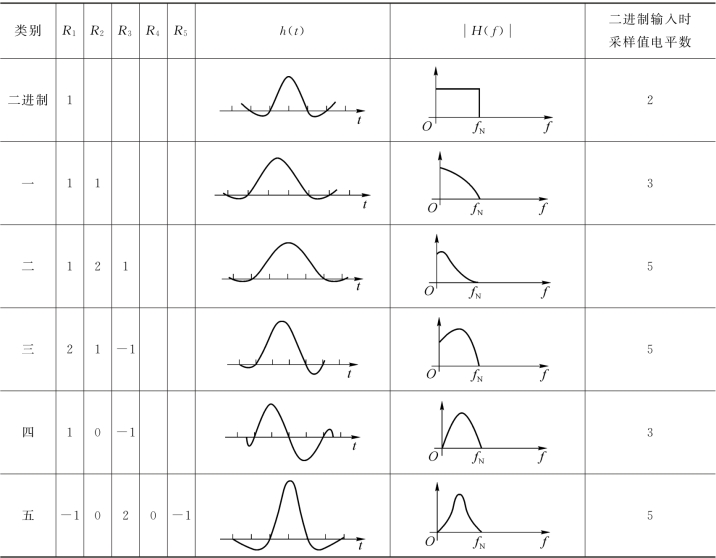
从前述讨论可知，部分响应系统有如下特点:

·有码间干扰，但是固定的，在接收端可以消除;

·频带利用率能达到2 Baud/Hz的极限;

·形成波形的前导和后尾衰减较快，降低了对收端定时的精度要求;

·物理上可实现;

·接收信号电平数大于发送信号电平数，抗干扰性能要差一些。