2.3.2 数字调幅
以基带数据信号控制一个载波的幅度,称为数字调幅,又称幅移键控,简写为ASK。
1.二进制数字调幅
(1)基本原理
通常,二进制数字调幅(2ASK)信号的产生方法有两种:相乘法和键控法,如图2-22所示。相乘法是将基带信号s(t)与载波相乘,而键控法是用基带信号s(t)控制载波的开关电路,此时的已调信号一般称为通断键控信号(OOK)。
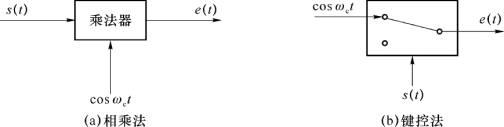
图2-22 2ASK的调制方法
下面以相乘法产生2ASK信号为例,分析其2ASK信号波形及功率谱。设用于调制的信号为s(t),则已调信号可以表示为
![]()
其中,s(t)可以是基带形成信号,也可以是数据终端发出的单、双极性矩形脉冲等形式的信号。为了分析方便,当调制信号s(t)分别是单极性不归零信号和双极性不归零信号时,将调制信号和已调信号波形画于图2-23(假设载波频率与码元速率的关系为f c=2f s)。
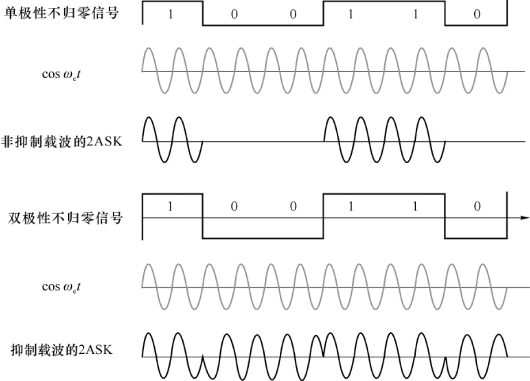
图2-23 2ASK信号波形
(2)2ASK信号功率谱密度
若设s(t)的功率谱密度为p S(f),则已调信号e(t)的功率谱p E(f)可以表示为
![]()
由此可见,若p S(f)确定,则p E(f)也可确定。下面分别讨论s(t)为单极性不归零信号和双极性不归零信号时,已调信号的功率谱密度。为了简便起见,假设“1”码和“0”码等概出现,且前后码元独立。
①s(t)为单极性不归零信号时
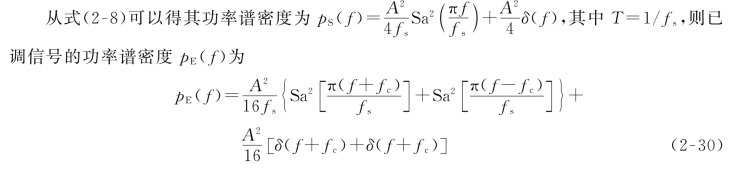
其功率谱如图2-24所示。可见,2ASK信号的功率谱密度也由连续谱和离散谱两个部分组成,基带信号的连续谱经调制后形成了双边带谱,离散谱则由基带信号的离散谱确定。其中假设载波频率f c较大,p S(f+f c)和p S(f-f c)在频率轴上没有重叠部分。
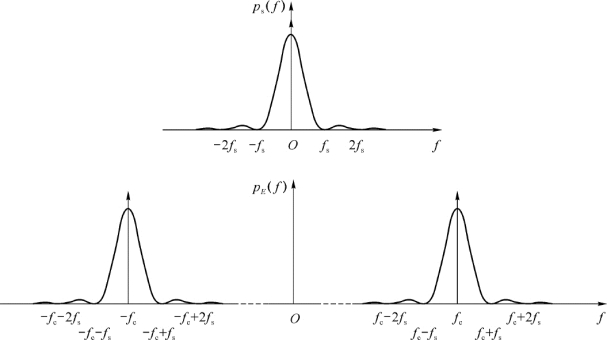
图2-24 非抑制载波的2ASK已调信号功率谱密度示意图
②s(t)为双极性不归零信号时
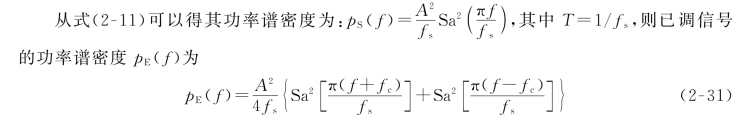
其功率谱如图2-25所示。由于双极性不归零信号中不含有直流分量,所以已调信号的功率谱中,在载波频率处就不含有离散谱分量,这称为抑制载波的2ASK调制。
总结2ASK调制的特点如下:
·实现了双边带调制;(https://www.daowen.com)
·调制信号功率谱密度决定了已调信号的功率谱密度;
·调制后的带宽为基带信号带宽的2倍。
(3)单边带和残余边带调制
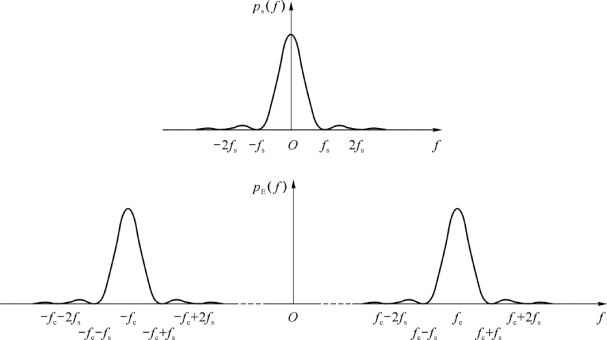
图2-25 抑制载波的2ASK已调信号功率谱密度示意图
2ASK信号具有两个边带,并且两个边带含有相同的信息。为了提高信道频带利用率,可以使用带通滤波器切除一个边带分量,即实现单边带传输,使得频带利用率是双边带传输的两倍。然而从图2-24和图2-25来看,有些基带信号含有丰富的低频分量,需要在载频f c处用尖锐截止的滤波器才能滤除其中一个边带,从而增加了滤波器的制作难度。实际中,在调制前要对基带信号进行处理,目的是使其不含直流分量,同时低频分量尽可能小。例如,采用2.2节中介绍的第四类部分响应系统,如图2-26所示,已调信号的功率谱在上、下边带之间有一个明显的分界,且无离散谱分量。
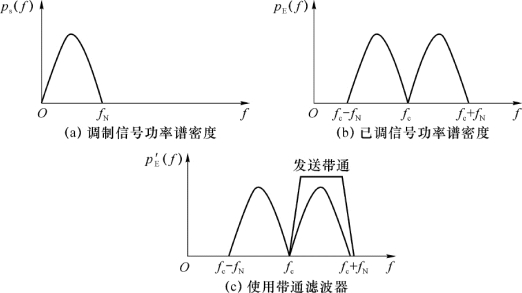
图2-26 单边带调制示意图
残余边带调制是介于双边带和单边带之间的一种调制方法,它是使已调双边带信号通过一个残余边带滤波器,使其双边带中的一个边带的绝大部分和另一个边带的小部分通过,形成所谓的残余边带信号。残余边带信号所占的频带大于单边带,又小于双边带,所以残余边带系统的频带利用率也是小于单边带,大于双边带的频带利用率,如图2-27所示。
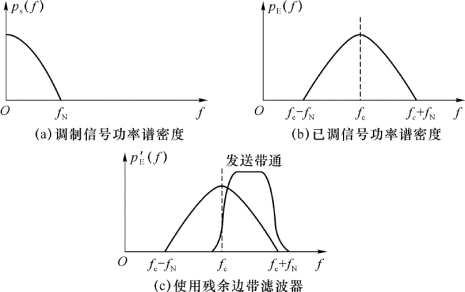
图2-27 残余边带调制示意图
单边带和残余边带调制曾用于中、高速调制解调器,后来被正交幅度调制QAM取代(详见2.3.5小节)。
2.多进制数字调幅
多进制数字调幅(MASK)是利用多进制数字基带信号去调制载波的幅度,在原理上可以看成是OOK方式在多进制上的推广。其调制信号(单极性)和已调信号波形如图2-28所示。
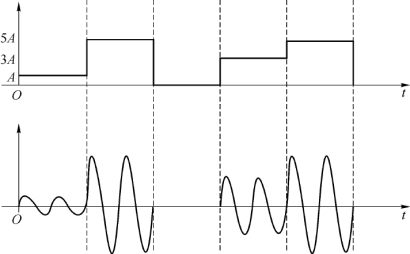
图2-28 MASK信号波形
由于MASK已调信号的幅度有M种可能的取值,与2ASK相比,MASK具有高效率的特点。即在相同的码元速率下,多进制系统的信息传输速率是二进制系统的信息传输速率的log2M倍,且可以证明MASK和2ASK已调信号的带宽相同。但是多进制调幅的抗噪声能力不强,要获得和2ASK相同的误码率,需要增加系统的发送功率。目前,实用的多进制调幅形式有多进制残留边带调制、多电平正交幅度调制等。
3.已调信号的星座图表示
MASK调制是多进制幅度调制,其已调信号可以写成:其中,A m=(2m+1-M)A,m=0,1,…,M-1,2A是两相邻信号幅度之间的差值,假设g(t)为单位矩形脉冲的简单情况,每个已调信号的波形可携带log2M比特的信息。
![]()
若以未调载波的相位作为基准相位或参考相位,则MASK已调信号相位有两种,即0°和180°,其幅度是A m。将已调信号映射到二维信号空间,用矢量来表示,则可以得到如图2-29(a)的矢量图,若只画出矢量的端点,则得到相应的星座图表示,如图2-29(b)所示。
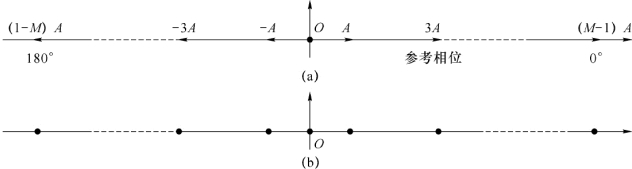
图2-29 MASK信号的矢量图与星座图
星座图是某种调制方式的信号点在信号空间分布的一种直观表示,对于判断该调制方式和比较不同调制方式的误码率等有很直观的效用。例如,星座图上各信号点之间的距离越大,抗误码能力越强。
