3.3.1 汉明码

虚拟实验
汉明码是一种能够纠正1位错码且编码效率较高的线性分组码。它是1950年由美国贝尔实验室提出来的,是第一个设计用来纠正差错的线性分组码,汉明码及其变型已广泛应用于数据存储系统中作为差错控制码。
1.(n,k)汉明码
在前面讨论奇偶校验时,如按偶校验,由于使用了1位监督位a 0,故它就能和信息位a n-1,a n-2,…,a 1一起构成一个代数式,如式(3-6)所示。在接收端解码时,实际上就是在计算
![]()
式(3-10)称为监督关系式(也叫监督方程),S称为校正子(校正子的个数与r相等)。若S=0,则无错;若S=1,则有错。由于校正子S的取值只有两种,它就只能代表“有错”和“无错”这两种信息,而不能指出错码的位置。不难推想,若监督位增加1位,即变成2位,则能增加一个类似于式(3-10)的监督关系式。由于两个校正子的可能值有4种组合:00,01,10,11,故能表示4种不同信息。若用其中1种表示无错,则其余3种就有可能用来指示一位错码的3种不同位置。同理,r个监督关系式能指示一位错码的(2r-1)个可能位置。
一般来说,若码长为n,信息位数为k,则监督位数r=n-k。若希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能位置,则要求
![]()
设分组码(n,k)中k=4,为了纠正1位错码,由式(3-11)可知,要求监督位数r≥3。若取r=3,则n=k+r=7,这就是(7,4)汉明码。
2.(7,4)汉明码
(7,4)汉明码的码组为a 6a 5a 4a 3a 2a 1a 0,其中a 6a 5a 4a 3是信息码,a 2a 1a 0是监督码。
(1)(7,4)汉明码的纠检错
(7,4)汉明码r=3,所以有3个校正子,用S 1,S 2,S 3表示3个监督关系式中的校正子。规定S 1,S 2,S 3的值与错码位置的对应关系如表3-4所列(自然,我们也可以规定成另一种对应关系,这不影响讨论的一般性)。
表3-4 较正子与错码位置

由表3-4的规定可知,当发生1个错码,其位置在a 2,a 4,a 5或a 6时,校正子S 1为“1”;否则“0”。这就意味着a 2,a 4,a 5和a 64个码元构成偶数监督关系,即
![]()
同理,a 1,a 3,a 5和a 6以及a 0,a 3,a 4和a 6也分别构成偶数监督关系,于是有
![]()
纵上所述,(7,4)汉明码是这样纠检错的:接收端收到某个(7,4)汉明码的码组,首先按照式(3-12)、式(3-13)和式(3-14)计算出校正子S 1,S 2,S 3,然后根据表3-4便可知道此(7,4)汉明码是否有错以及差错的确切位置,既而纠正差错。
例3-1 接收端收到某(7,4)汉明码为1001010,此(7,4)汉明码是否有错?错码位置为哪一位?
解 计算较正子
S 1=a 6⊕a 5⊕a 4⊕a 2=1⊕0⊕0⊕0=1(https://www.daowen.com)
S 2=a 6⊕a 5⊕a 3⊕a 1=1⊕0⊕1⊕1=1
S 3=a 6⊕a 4⊕a 3⊕a 0=1⊕0⊕1⊕0=0
较正子为110,根据表3-4可知此(7,4)汉明码有错,错码位置为a 5。
这里有一个问题需要说明:从表3-4可以看出,(7,4)汉明码无论是信息码还是监督码有错,都能够检测出来,即r个监督码对整个码组的n个码元都起监督作用。
(2)(7,4)汉明码的产生
以上我们知道了(7,4)汉明码是如何纠检错的了,但是(7,4)汉明码是如何产生的呢?下面加以介绍。
在发送端进行编码时,信息位a 6,a 5,a 4,a 3是数据终端输出的,它们的值是已知的。而监督位a 2,a 1,a 0应根据信息位的取值按监督关系来确定,即监督位应使式(3-12)、式(3-13)和式(3-14)中的校正子S 1,S 2,S 3均为零(表示码组中无错,是正确的码组),于是有下列方程组
由上式经移项运算,解出监督位为


已知信息位后,就可直接按式(3-16)计算出监督位。3个监督位附在4个信息位后面便可得到(7,4)汉明码的整个码组。由此可得出(7,4)汉明码的24=16个许用码组,如表3-5所示。
表3-5 (7,4)汉明码的许用码组
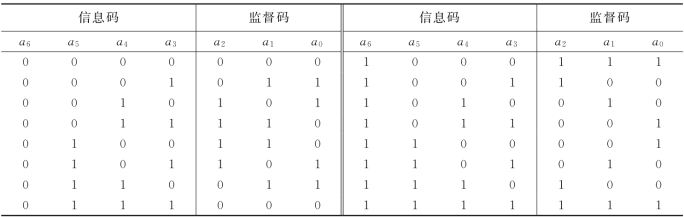
例3-2 已知信息码为1101,求所对应的(7,4)汉明码。
解 由式(3-16)求监督码
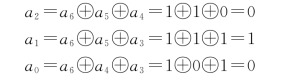
此(7,4)汉明码为1101010。
(3)(7,4)汉明码的汉明距离及编码效率
①汉明距离
汉明码属于线性分组码,根据线性分组码的性质可以求出(7,4)汉明码的汉明距离d min=3(线性分组码的概念及性质见后)。因此,由式(3-2)和式(3-3)可知,这种码能纠正1个错码或检测2个错码。
②编码效率
(7,4)汉明码的编码效率为
![]()
可以算出,当n很大时,(7,4)汉明码的编码效率接近于1。与码长相同的能纠正1位错码的其他分组码比,汉明码的编码效率最高,且实现简单。因此,至今在码组中纠正1个错码的场合还广泛使用。
