3.3.2 线性分组码
前面已经提到,线性码是指监督码元与信息码元之间满足一组线性方程的码;分组码是监督码元仅对本码组中的码元起监督作用,或者说监督码元仅与本码组的信息码元有关。既是线性码又是分组码的编码就叫线性分组码。
在差错控制编码中,线性分组码是非常重要的一大类码,前面所介绍的各种差错控制编码都属于线性分组码。下面研究线性分组码的一般问题。
1.监督矩阵
这里以(7,4)汉明码为例引出线性分组码监督矩阵的概念。
式(3-15)就是一组线性方程,现在将它改写成
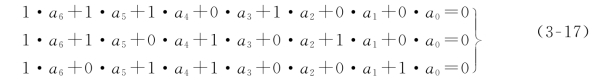
式(3-17)中已将“⊕”简写为“+”,仍表示“模2加”,本章以后各部分除非另加说明,这类式中的“+”都指“模2加”。式(3-17)还可以写成矩阵形式
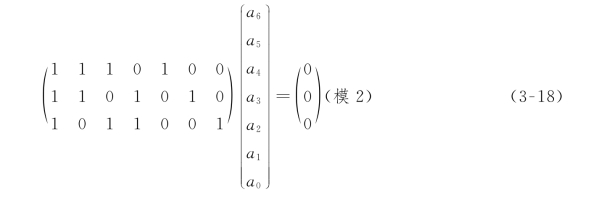
令
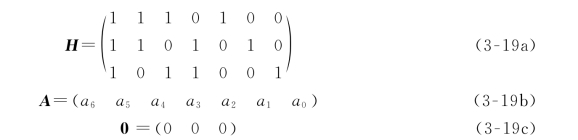
式(3-18)可以简记为
![]()
右上标“T”表示将矩阵转置。例如,H T是H的转置,即H T的第一行为H的第一列,H T的第二行为H的第二列等。由于式(3-17)来自监督方程,因此称H为线性分组码的监督矩阵。从式(3-17)和式(3-18)都可看出,H的行数就是监督关系式的数目,它等于监督位的数目r,而H的列数就是码长n,这样H为r×n阶矩阵。监督矩阵H的每行元素“1”表示相应码元之间存在着监督关系,由此各监督码元是共同对整个码组进行监督,称为一致监督。例如,H的第一行1110100表示监督位a 2是由信息位a 6,a 5,a 4之和(模二和)决定的。
式(3-19a)中的监督矩阵H可以分成两部分
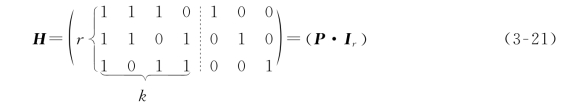
其中,H为r×n阶矩阵,I r为r×r阶单位方阵。我们将具有[P·I r]形式的H矩阵称为典型形式的监督矩阵。
类似于式(3-15)改变成式(3-18)中矩阵形式那样,式(3-16)也可以改写成
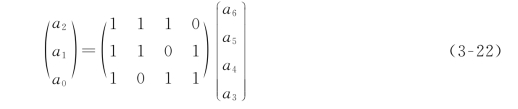
比较式(3-21)和式(3-22),可以看出式(3-22)等式右边前部矩阵即为P。对式(3-22)两侧作矩阵转置,得
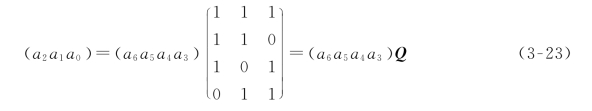
其中,Q为一k×r阶矩阵,它是矩阵P的转置,即
![]()
式(3-23)表明,信息位给定后,用信息位的行矩阵乘Q矩阵就可计算出各监督位,即
![]()
纵上所述,可以得到一个结论,已知信息码和典型形式的监督矩阵H,就能确定各监督码元。具体过程为:由H根据式(3-21)得出矩阵P,然后求P的转置Q,再根据式(3-25)即可求出监督码。
值得说明的是,虽然式(3-25)是由(7,4)汉明码推导得出的,但这个公式适合所有的线性分组码。
由线性代数理论得知,H矩阵的各行应该是线性无关的,否则将得不到r个线性无关的监督关系式,从而也得不到r个独立的监督码位。若一矩阵能写成典型矩阵形式[P·I r],则其各行一定是线性无关的。因为容易验证单位方阵[I r]的各行是线性无关的,故[P·I r]的各行也是线性无关的。
2.生成矩阵
要求得整个码组,我们将Q的左边加上一个k×k阶单位方阵,就构成一个新的矩阵G,即

式(3-26)的G称为典型的生成矩阵,由它可以产生整个码组A,即有
![]()
因此,若找到了码的典型的生成矩阵G,则编码的方法就完全确定了。由典型的生成矩阵得出的码组A中,信息位不变,监督位附加于其后,这种码称为系统码。
以(7,4)汉明码为例可以验证式(3-27)的正确性。上述可知(7,4)汉明码的Q矩阵为
 (https://www.daowen.com)
(https://www.daowen.com)
由式(3-26)可求出(7,4)汉明码典型的生成矩阵为

取表3-5中第3个码组中的信息码0010,根据式(3-27)可求出整个码组A为
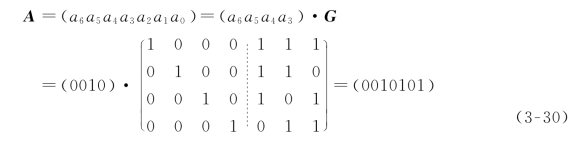
可见,所求得的码组正是表3-5中第3个码组。
与H矩阵相似,我们也要求生成矩阵G的各行是线性无关的。因为由式(3-27)可以看出,任一码组A都是G的各行的线性组合。G共有k行,若它们线性无关,则可组合出2k种不同的码组A,它们恰好是有k位信息位的全部码组;若G的各行线性相关,则不可能由G生成2k种不同的码组了。
实际上,G的各行本身就是一个码组。下面还是以(7,4)汉明码为例说明这一点,在式(3-29)中,若a 6a 5a 4a 3=1000,则码组A就等于G的第一行;若a 6a 5a 4a 3=0100,则码组A就等于G的第二行;等等。因此,若已有k个线性无关的码组,则可以用其作为生成矩阵G,并由它生成其余的码组。
线性代数理论还指出,非典型形式的生成矩阵若它的各行是线性无关的,则可以经过运算化成典型形式。因此,若生成矩阵是非典型形式的,则首先转化成典型形式后,再用式(3-27)求得整个码组。
3.监督矩阵与生成矩阵的关系
典型的监督矩阵H与典型的生成矩阵G之间的关系可用式(3-21)、式(3-24)和式(3-26)表示,为方便读者学习,现重写于下:
H=[P·I r],Q=P T,G=[I kQ]
例3-3 某(7,4)线性分组码,监督方程如下,求监督矩阵H和典型的生成矩阵G。如信息码为0010,求整个码组A。
a 2=a 6⊕a 5⊕a 3
a 1=a 6⊕a 4⊕a 3
a 0=a 5⊕a 4⊕a 3
解 将已知监督方程改写为
1·a 6⊕1·a 5⊕0·a 4⊕1·a 3⊕1·a 2⊕0·a 1⊕0·a 0=0
1·a 6⊕0·a 5⊕1·a 4⊕1·a 3⊕0·a 2⊕1·a 1⊕0·a 0=0
0·a 6⊕1·a 5⊕1·a 4⊕1·a 3⊕0·a 2⊕0·a 1⊕1·a 0=0
由此可得出监督矩阵H为
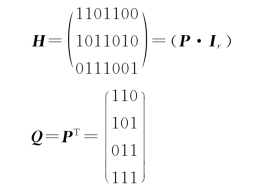
典型的生成矩阵G为
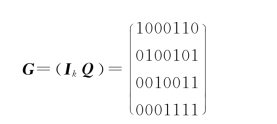
信息码为0010时,整个码组A为
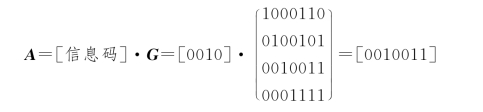
4.线性分组码的主要性质
线性分组码具有如下一些主要性质。
(1)封闭性
所谓封闭性,是指一种线性分组码中的任意两个码组之逐位模2加仍为这种码中的另一个许用码组。这就是说,若A 1和A 2是一种线性分组码中的两个许用码组,则A 1+A 2仍为其中的另一个许用码组。这一性质的证明很简单,若A 1,A 2为许用码组,则按式(3-20)有
A 1·H T=0,A 2·H T=0
将上两式相加,可得
A 1·H T+A 2·H T=(A 1+A 2)·H T=0
可见,A 1+A 2必定也是一许用码组。
(2)码的最小距离等于非零码的最小重量
因为线性分组码具有封闭性,因而两个码组之间的距离必是另一码组的重量,故码的最小距离即是码的最小重量(除全“0”码组外)。
