3.4.1 循环码的循环特性
循环码属于线性分组码，它除了具有线性分组码的一般性质外，还具有循环性。在具体研究循环码的循环性之前，我们首先要了解码的多项式的含义。
1.码的多项式
为了便于用代数理论来研究循环码，把长为n的码组与n-1次多项式建立一一对应的关系，即把码组中各码元当作是一个多项式的系数，若码组A=(a n-1，a n-2…a 1，a 0)，则相应的多项式表示为
这种多项式中，x的幂次仅是码元位置的标记。多项式中x i的存在只表示该对应码位上是“1”码，否则为“0”码，我们称这种多项式为码的多项式。由此可知码组和码的多项式本质上是一回事，只是表示方法不同而已。
例如，一个码组为A=1011011，它所对应的多项式为
A(x)=x 6+x 4+x 3+x+1
2.循环码的循环特性
循环码的循环性是指循环码中任一许用码组经过循环移位后(将最右端的码元移至左端，或反之)所得到的码组仍为它的一个许用码组。
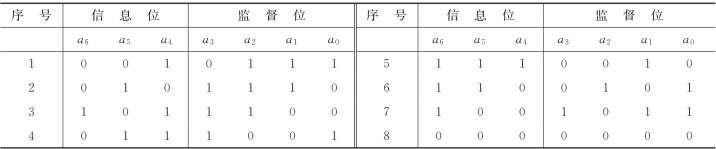
表3-6给出一种(7，3)循环码的全部码组，由此表可直观看出这种码的循环性。例如，表中的第2个码组向右循环移一位即得到第5个码组，第2个码组向左循环移一位即得到第3个码组。
表3-6 (7,3)循环码的一种码组
表3-6中的(7，3)循环码中的任一码组(a 6，a 5，…，a 1，a 0)所对应的多项式可以表示为
对于循环码，一般来说，若A=(a n-1，a n-2，…，a 1，a 0)是一个(n，k)循环码的码组，则
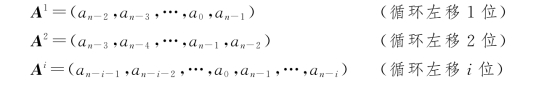
也都是该编码中的码组(A的上标i表示移位次数)。它们所对应的多项式分别为
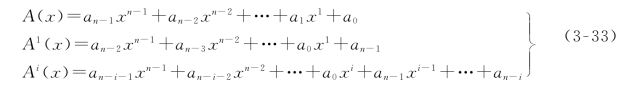
我们来看A 1(x)，它等于x A(x)用x n+1多项式除后所得余式，即注意，在模2运算中可用加法代替减法。
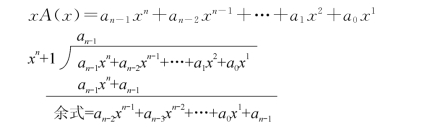
依此类推，可以得到一个重要结论:在循环码中，若A(x)对应一个长为n的许用码组，则x iA(x)用x n+1多项式除后所得余式为A i(x)(习惯说成按模x n+1运算)，它对应的码组也是一个许用码组。记作
以上介绍了循环码的循环性，借助于其循环性，已知一个码组，可以很方便地求出其他许用码组，下面举例说明。
例3-4 已知(7，3)循环码的一个许用码组，试将所有其余的许用码组填入下表。
解 将表中所给第1个码组循环左移一位后得到第2个码组，第2个码组循环左移一位后得到第3个码组，依此类推，可得到第4个码组～第7个码组，第8个码组为全“0”。
