2.3.7 数字信号的最佳接收
1.最佳接收的概念
通信系统中信道特性的不理想及信道噪声的存在，会直接影响接收系统的性能，而一个通信系统的质量优劣在很大程度上取决于接收系统的性能。把接收问题作为研究对象，研究在噪声条件下如何最好地提取有用信号，且在某个准则下构成最佳接收机，使接收性能达到最佳，这就是通信理论中十分重要的最佳接收。
最佳接收是从提高接收机性能角度出发，研究在输入相同信噪比的条件下，如何使接收机最佳地完成接收信号的任务。因此要研究最佳接收机的原理，讨论它们在理论上的最佳性能，并与现有各种接收方法比较。这里“最佳”或“最好”并不是一个绝对的概念，而是在相对意义上说的，使之在某一个“标准”或“准则”下是最佳，而对其他条件下，不同的准则也可能是等效的。数字通信中常用的“最佳”准则是指最小差错概率准则、最小均方误差准则、最大输出信噪比准则等。
2.最小差错概率准则
在数字通信中最直观和最合理的准则应该是“最小差错概率准则”。在数字通信系统中，假设发送消息的信号空间为{s1，s2，…，sm}，若在传输过程中没有任何干扰以及其他可能的畸变，则在发送端就一定能够被无差错地做出相应判决结果{y 1，y 2，…，y m}，注意这里信号空间和所期望的判决结果空间是一一对应的。实际上，由于信道畸变和传输系统引入的噪声，这种理想情况是不可能发生的，例如发送si而可能判为非y i的任何一个，即存在错误接收和判决。
为简便起见，以m=2即二进制数字信号接收为例(“1”码发信号s1，“0”码发信号s2)，讨论最佳接收准则。此时，传输差错率为
其中，P(s 1)和P(s 2)为先验概率，即发送s 1和发送s 2的概率;P(y 2|s 1)和P(y 1|s 2)为错误概率，即发送s1而判决成y 2的概率和发送s2而判决成y 1的概率。这样即可得到一个最简单的最小差错概率准则，从而去设计一个最佳接收系统，使得传输发生差错的概率最小。
3.二进制确知信号的最佳接收
在数据通信中，所传输的信号波形形式是确定的，如2PSK中的A cosωct表示“1”;A cos(ωct+π)表示“0”。因此，接收端的任务是在一个码元间隔时间T s内确定发送的是哪一个确知信号，即在有噪声和信道畸变情况下，以最小错误概率来对信号进行判决。
较为简单的情况是二进制确知信号的最佳接收。假设接收机收到的两个可能信号为s1(t)和s2(t)，即“1”码信号为s1(t)，“0”码信号为s2(t)，系统中的噪声为加性高斯白噪声n(t)。这时，在0～T s时间内，接收到的信号y(t)可写成
其中，s(t)可能是s 1(t)或者是s2(t)，即y(t)=s1(t)+n(t)或y(t)=s2(t)+n(t)。
接收机预先知道s 1(t)和s 2(t)的具体波形，但需要判断在0～T s内收到的究竟是哪一个。所以，接收机的任务是根据0～T s内收到的y(t)来判定信号是s1(t)还是s2(t)，从而判定是“1”码还是“0”码。这里，最佳接收方法是使在高斯白噪声环境中的判决误码率最小。
则判为s2(t)出现，即认为发送端发送的是“0”码。这一准则就是最小均方误差准则。式(2-55)和式(2-56)的物理意义是:y(t)与s1(t)的均方误差小时，y(t)波形更像s1(t)，所以判为“1”;y(t)与s2(t)的均方误差小时，y(t)波形更像s2(t)，所以判为“0”。
按最小均方误差准则构成的接收机即为最佳接收机，其构成如图2-56所示。
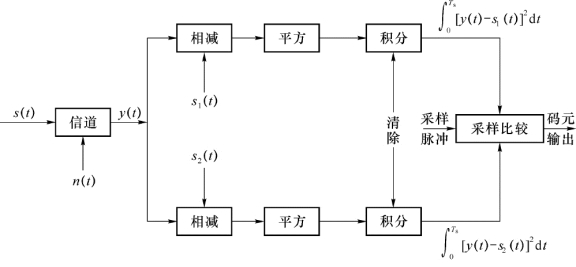
图2-56 最佳接收机构成示意图
式(2-55)和式(2-56)的平方项展开可有
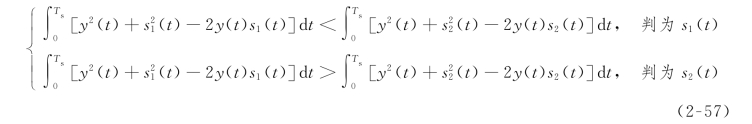
对于许多实际通信系统，如采用抑制载波的2ASK、PSK等调制方式时，则到达接收机的两个确知信号s1(t)和s2(t)的持续时间相同，且有相等的能量，即
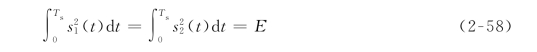
将式(2-58)代入式(2-57)，则展开式(2-57)可变为下述判别式
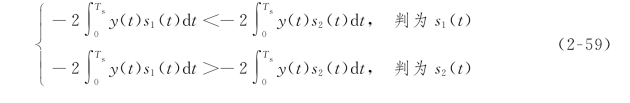
去掉式(2-59)不等式两边的负号，则大于、小于号反向，则有
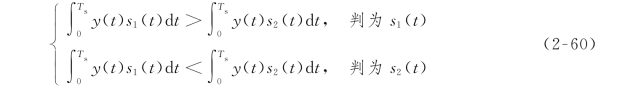
这一判别式称为相关接收判别式，其物理意义为: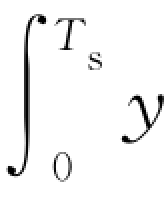
(t)s(t)d t的值表示两个信号的相关程度，y(t)与s1(t)的相关性大时，y(t)波形更像s1(t)，所以判决为“1”码;y(t)与s2(t)的相关性大时，y(t)波形更像s2(t)，所以判决为“0”码。
按式(2-60)构成的接收机称为相关接收机，其构成如图2-57所示。
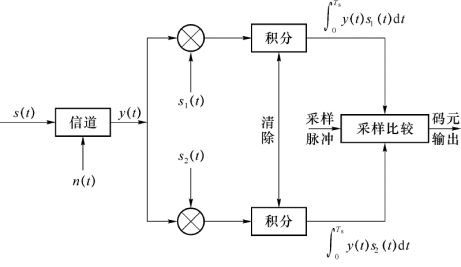
图2-57 相关接收机构成示意图
4.最佳接收时的误码率
图2-57中的两个积分器输出用u 1(T s)和u 2(T s)表示，即
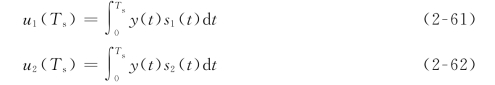
图中采样比较可视为相减电路，即
此时，判决规则为:D＞0时判为“1”，D＜0时判为“0”。
若输入信号为y(t)=s(t)+n(t)，则D中应包括两部分:一部分来自信号s(t);另一部分来自噪声n(t)，这时式(2-63)可写为
当输入信号为y(t)=s1(t)+n(t)时，
令ρ为相关系数，则ρ可以表示为
则有
由于n(t)是均值为零的高斯噪声，所以D n是一个均值为零的随机变量，其概率密度函数为
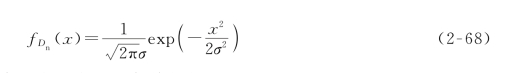
其中，σ2=N 0E(1-ρ)，N 0为高斯白噪声的功率谱密度。
当没有噪声时，即D n=0，因为ρ＜1，所以
根据式(2-63)的判决准则，总能正确判为“1”，即不存在误码。当有噪声时，由于D n为随机变量，可取任意值，当D n落在(-∞，-D s]之间时，就将其错判为“0”码，即引起误码。其误码概率为
再将σ2=N 0E(1-ρ)带入式(2-72)，则有
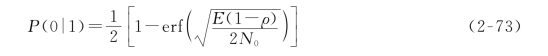
同理，可求得输入信号为y(t)=s 2(t)+n(t)时，误判为“1”码的概率P(1|0)。
当s 1(t)和s 2(t)的码元能量相同时，可得P(0|1)=P(1|0)，于是总误码率为
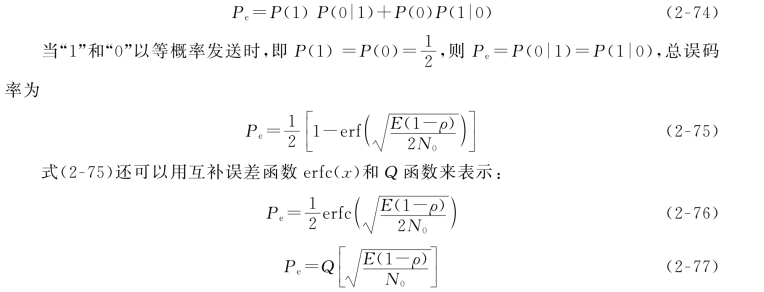
5.二进制数字调相的误码率
下面以2PSK调制为例，计算其在最佳接收时的误码率。
2PSK信号表示为:“1”码对应的波形为s1(t)=A cos(ωct+θ);“0”码对应的波形为s 1(t)=-A cos(ωct+θ)，则由式(2-77)得
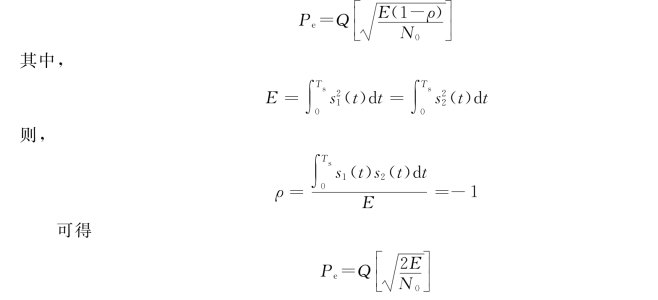
在给定E和N 0的条件下，查Q函数表，即可求得误码率。
例2-5 某卫星传输气象云图数据系统，速率为1.75 Mbit/s，采用2PSK调制方式。假设N 0=1.26×10-20W/Hz，若总的传输损失为144 dB。试求P e=10-7时，最小的卫星发射功率应为多少?
