3.4.3 循环码的编码方法
编码的任务是在已知信息位的条件下求得循环码的码组,而我们要求得到的是系统码,即码组前k位为信息位,后n-k位是监督位。设信息位对应的码的多项式为
![]()
其中,系数mi为1或0。
我们知道(n,k)循环码的码的多项式的最高幂次是n-1次,而信息位是在它的最前面的k位,因此信息位在循环码的码多项式中应表现为多项式x n-km(x)(最高幂次为n-k+k-1=n-1)。显然
![]()
它从幂次x n-k-1起至x 0的n-k位的系数都为0。
如果用g(x)去除x n-km(x),可得

其中,q(x)为幂次小于k的商多项式,而r(x)为幂次小于n-k的余式。
式(3-48)可改写成
![]()
式(3-49)表明:多项式x n-km(x)+r(x)为g(x)的倍式。根据式(3-37)或式(3-38),x n-km(x)+r(x)必定是由g(x)生成的循环码中的码组,而余式r(x)即为该码组的监督码对应的多项式。
根据上述原理,编码步骤可归纳如下。
(1)用x n-k乘m(x)得到x n-km(x)
这一运算实际上是把信息码后附上n-k个“0”。例如,信息码为110,它相当于m(x)=x 2+x。当n-k=7-3=4时,x n-km(x)=x 4(x 2+x)=x 6+x 5,它相当于1100000。(https://www.daowen.com)
(2)用g(x)除x n-km(x),得到商q(x)和余式r(x),即
![]()
例如,若选用g(x)=x 4+x 2+x+1作为生成多项式,则
![]()
显然,r(x)=x 2+1。
(3)求多项式A(x)=x n-km(x)+r(x)
![]()
式(3-51)对应的码组即为本例编出的码组A=1100101,这就是表3-6中的第7个码组。读者可按此方法编出其他码组。可见,这样编出的码就是系统码了。
上述编码方法,在用硬件实现时,可以由除法电路来实现。除法电路的主体由一些移位寄存器和模2加法器组成,码的多项式中x的幂次代表移位的次数,例如,图3-6给出了上述(7,3)循环码编码器的组成。
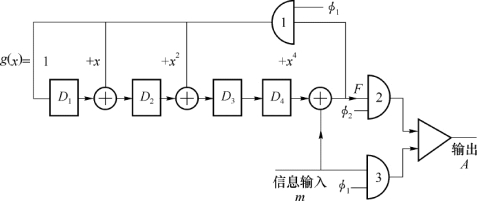
图3-6 (7,3)循环码编码器的组成
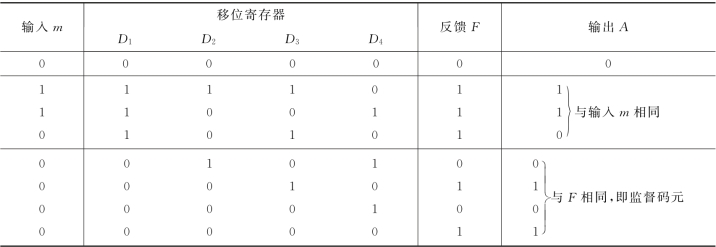
图中对应g(x)有4级移位寄存器,分别用D 1,D 2,D 3和D 4表示。g(x)多项式中系数是1或0表示该位上反馈线的有无,另外,图中信号φ1和φ2控制门电路1~3。当信息位输入时,控制信号使门1、门3打开,门2关闭,输入信息码元一方面送入除法器进行运算,另一方面直接输出。在信息位全部进入除法器后,控制信号使门1、门3关闭,门2打开,这时移位寄存器通过门2直接输出,将移位寄存器中存储的除法余项依次取出,即将监督码元附加在信息码元之后。因此,编出的码组前面是原来的k个信息码元,后面是(n-k)个监督码元,从而得到系统分组码。为了便于理解,上述编码器的工作过程示于表3-7。这里设信息码元为110,编出的监督码元为0101,循环码组为1100101。
表3-7 (7,3)循环码编码器的工作过程
顺便指出,由于微处理器和数据信号处理器的应用日益广泛,目前一般采用这些先进器件和相应的软件来实现上述编码。
