3.2.1　奇偶监督码

3.2.1　奇偶监督码

奇偶监督码是最简单的一种检错码，又称奇偶校验码，在数据通信中得到广泛的应用。其编码规则是先将所要传输的数据码元(信息码)分组，在分组信息码元后面附加1位监督码，使得该码组中信息码与监督码合在一起“1”的个数为偶数(称为偶校验)或奇数(称为奇校验)，表3-1是按照偶监督规则插入监督位的。

表3-1　奇偶监督码举例

在接收端检查码组中“1”的个数，若发现不符合编码规律，则说明产生了差错，但是不能确定差错的具体位置，即不能纠错。

奇偶监督码的这种监督关系可以用公式表示。设码组长度为n，表示为(a n-1，a n-2，…，a 1，a 0)，其中前n-1位为信息码元，第n位为监督位a 0。在偶检验时有

其中，⊕表示模2加，监督码元a 0可由下式产生

在奇校验时有

监督码元a 0可由下式产生

这种奇偶检验只能发现单个或奇数个差错，而不能检测出偶数个差错，因而它的检错能力不高，但这并不表明它对随机奇数个差错的检错率和偶数个差错的漏检率相同。由式(3-5)容易证明，当n≪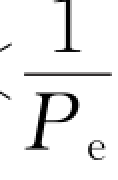时，出错位数为2t-1奇数的概率总比出错位数为2t偶数(t为正整数)的概率大得多，即错1位码的概率比错2位码的概率大得多，错3位码的概率比错4位码的概率大得多。因此，绝大多数随机差错都能用简单奇偶检验查出，这正是奇偶校验码被广泛用于以随机差错为主的数据通信系统的原因。但这种奇偶校验码难于对付突发差错，所以在突发差错很多的信道中不能单独使用。最后指出，奇偶校验码的最小码距为d min=2。