3.5.1 卷积码的基本概念
1.卷积码的概念
在分组码中,任何一段规定时间内编码器产生的n个码元的一个码组,其监督位完全决定于这段时间中输入的k个信息位,这个码组中的n-k个监督位仅对本码组起监督作用。
卷积码则不然,编码器在任何一段规定时间内产生的n个码元,其监督位不仅取决于这段时间中的k个信息位,而且还取决于前N-1段规定时间内的信息位。换句话说,监督位不仅对本码组起监督作用,还对前N-1个码组也起监督作用。
这N段时间内的码元数目n N称为这种卷积码的约束长度。通常把卷积码记作(n,k,N),其编码效率为R=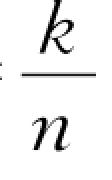 。
。
2.卷积码的编码
下面我们通过一个简单例子来说明卷积码的编码和解码原理,图3-10是一个简单的卷积码的编码器,它由两个移位寄存器D 1,D 2和模2加电路组成。
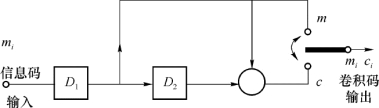
图3-10 简单的卷积码的编码器
图3-10所示编码器的输入信息位一方面可以直接输出,另一方面还可以暂存在移位寄存器中。每当输入编码器一个信息位,就立即计算出一个监督位,并且此监督位紧跟此信息位之后发送出去,如图3-11所示。
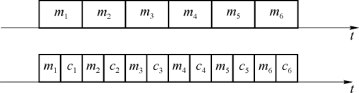
图3-11 编码器的输入与输出关系
编码器工作过程是这样的:移位寄存器按信息位的节拍工作,输入一位信息,电子开关倒换一次,即前半拍(半个输入码元宽)接通m端,后半拍接通c端。因此,若输入信息为m 1,m 2,m 3,…,则输出卷积码为m 1,c 1,m 2,c 2,m 3,c 3,…,其中ci为监督码元。由图3-11可见:
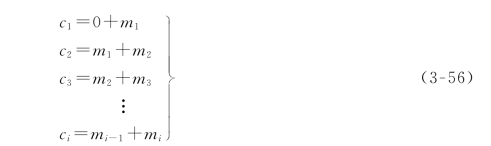
显然,卷积码的结构是:“信息码、监督码、信息码、监督码…”。本例中1个信息码与1个监督码组成一组,但每组中的监督码除了与本组信息码有关外,还与上一组信息码有关。或者说,每个信息码除受本组监督码监督外,还受下一组监督码的监督。本例中n=2,k=1,n-k=1,N=2,可记作(2,1,2)卷积码。
为理解卷积码编码器的一般结构,图3-12给出了它的一般形式,包括:一个由N段组成的输入移位寄存器,每段有k级,共Nk位寄存器;一组n个模2和加法器;一个由n级组成的输出移位寄存器。
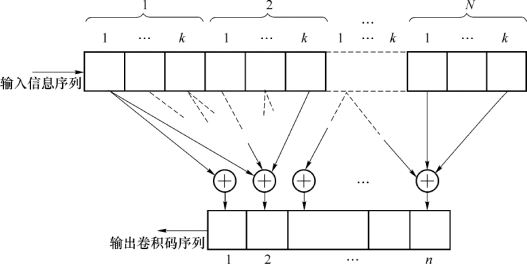
图3-12 卷积码编码器的一般形式
对应于每段k个比特的输入序列,输出n个比特。由图3-12可知,n个输出比特不但与当前的k个输入比特有关,而且与以前的(N-1)k个输入比特有关。整个编码过程可以看成是输入信息序列与由移位寄存器模2和连接方式所决定的另一个序列的卷积,故称为卷积码。(https://www.daowen.com)
3.卷积码的解码
现在来讨论卷积码的解码,一般说来,卷积码有两类解码方法:
·代数解码,这是利用编码本身的代数结构进行解码,不考虑信道的统计特性;
·概率解码,此种解码方法在计算时要用到信道的统计特性。
这里,我们先结合上例介绍门限解码原理。门限解码属于代数解码,它对于约束长度较短的卷积码最为有效,而且设备较简单,还可以应用于一些分组码的解码。可见,这种解码方法是有典型意义的。
图3-13是与图3-10对应的解码器。设接收到的码元序列为m′1c′1,m′2c′2,m′3c′3,…,解码器输入端的电子开关按节拍把信息码元与监督码元分接到m′端与c′端,3个移位寄存器的节拍比码序列的节拍低一倍。其中移位寄存器D 1,D 2在信息码元到达时移位,监督码元到达期间保持原状;而移位寄存器D 3在监督码元到达时移位,信息码元到达期间保持原状。移位寄存器D 1,D 2和模2加电路构成与发送端一样的编码器,它从接收到的信息码元序列中计算出对应的监督码元序列。模2加法器把上述计算的监督码元序列与接收到的监督码元序列进行比较:若两者相同,则输出“0”;若两者不同,则输出“1”。
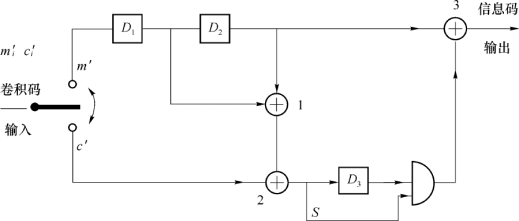
图3-13 与图3-10对应的解码器
显然,当按接收到的信息码元计算出的监督码元与实际收到的监督码元不符时,必定出现了差错,要确定差错的位置,将模2加法器输出记作S(校正子),根据图3-13可以写出S的方程为
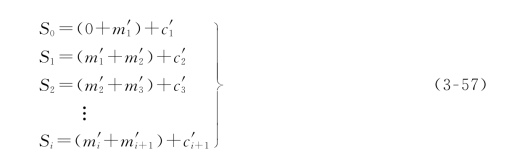
由式(3-57)可见,每个信息码元出现在两个S方程中。例如,m′2就与S 1和S 2有关,m′3就与S 2和S 3有关,……,m′i就与S i-1和Si有关。我们来分析m′2,在判决m′2是否有差错时,应根据S 1和S 2的值。决定S 1和S 2值的共有5个码元:m′1,m′2,m′3,c′2及c′3,但其中只有m′2与S 1和S 2两个值都有关,而其他码元只与一个值有关。这种情况称为方程S 1与S 2正交于m′2,或者说校验子方程S 1与S 2构成m′2的正交方程组。在差错不超过一个的条件下,根据正交性得到判决规则如下:
(a)当S 1,S 2都为“0”时,解码方程式(3-57)与编码方程式(3-56)完全一致,可判决无错;
(b)当S 1,S 2都为“1”时,必定是m′2出错,可判m′2有错(从而可纠正);
(c)当S1,S 2中只有一个“1”时,必定是m′1,m′3,c′2及c′3中有一个出错,所以可判决m′2无错。
对于其他信息码元也可根据两个相对应的S值来判决是否有错。
完成上述判决规则的电路就是图3-13中的移位寄存器D 3、与门及模2加法器3。例如,在判决m′2时,D 1寄存m′3,D 2寄存的是m′2,而D 3寄存的是S 1。当m′3到达时,模2加法器2中就输出S 2,与门判断S 1和S 2是否都是“1”。如果都是“1”,那么它的输出为“1”;否则输出为“0”。与门输出与D 3输出相加,即为m 2的解码输出。当S 1=S 2=1时,表示m′2有错,与门输出“1”,在模2加法器3中将该信码纠正;当与门输出为“0”时,表明m′2无错,将该信码输出。其余各信码的解码与纠错依此类推。在这一例子中可以看到,在解码时的正交方程组中,涉及5个码元,即3个码组,所以这个简单的卷积码可以在连续3个码组中纠正1位差错。
从以上介绍可以看出,卷积码是一种非分组码,但它是线性码。卷积码的构造比较简单,在性能上也相当优越。不过,正如前面所提到的,卷积码的数学理论尚不像循环码那样完整严密。
