3.4.4 循环码的解码方法
1.检错的实现
接收端解码的要求有两个:检错和纠错，达到检错目的的解码原理十分简单。由于任一码组的多项式A(x)都应能被生成多项式g(x)整除，所以在接收端可以将接收码组的多项式R(x)用原生成多项式g(x)去除。当传输中未发生差错时，接收码组与发送码组相同，即R(x)=A(x)，故接收码组的多项式R(x)必定能被g(x)整除;当码组在传输中发生差错时，R(x)≠A(x)，R(x)被g(x)除时可能除不尽而有余项，即有
因此，我们就以余项是否为零来判别码组中有无错码。这里还需指出一点，如果信道中错码的个数超过了这种编码的检错能力，恰好使有错码的接收码组能被g(x)所整除，这时的错码就不能检出了，这种差错称为不可检差错。
下面举例说明循环码的编码和解码。
例3-6 一组8比特的数据11100110(信息码)通过数据传输链路传输，采用CRC(循环冗余检验)进行差错检测，如采用的生成多项式对应的码组为11001，写出:
(a)监督码的产生过程;
(b)监督码的检测过程。
解 根据题意，信息码的码位k=8，由生成多项式对应的码组11001可写出生成多项式g(x)=x 4+x 3+1，由此得出n-k=4，所以n=12，故r=4。
对应于11100110(信息码)的监督码的产生如图3-7(a)所示。
开始，4个“0”被加于信息码末尾，这等于信息码的多项式乘以x 4。然后被生成多项式模2除，结果得到的4位(0110)余数即为监督码，把它加到11100110(信息码)的末尾发送。
在接收机上，整个接收的比特序列对应的多项式被同一生成多项式除，举两个例子如图3-7(b)所示。第一个例子中没发生差错，得到的余数为0;第二个例子中，在发送比特序列的末尾发生了4比特的突发差错，得到的余数不为0，说明传输出现差错。
图3-7 循环码的编码和解码过程举例
根据上述原理构成的解码器如图3-8所示。
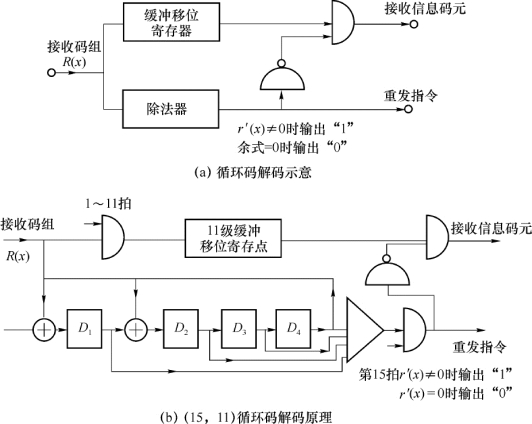
图3-8 循环码解码原理举例
由图3-8可见，解码器的核心就是一个除法电路和缓冲移存器，而且这里的除法电路与发送端编码器中的除法电路相同。若在此除法器中进行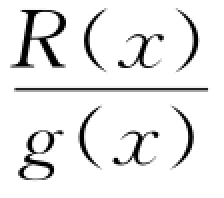
运算的结果，余项为0，则认为码组R(x)无错，这时将暂存于缓冲移存器的接收码组送出到解码器输出端;若运算结果余项不等于0，则认为R(x)中有错，但错在何位不知道，这时就可以将缓冲移存器中的接收码组删除，并向发送端发出一个重发指令，要求重发一次该码组。图3-8(b)中还给出了稍具体一些的(15，11)循环码的解码原理图，这里移位寄存器级数k=11，g(x)=x 4+x+1，在第n=15拍时检查余式r′(x)是否为0。当然，实际电路还要复杂些，图3-8只是用来说明循环码的检错功能。
2.纠错的实现
在接收端为纠错而采用的解码方法自然比检错时复杂。为了能够纠错，要求每个可纠正的差错图样必须与一个特定余式有一一对应关系。余式是指接收码组的多项式R(x)被生成多项式g(x)除后所得的余式r′(x)，这里解释一下差错图样的概念。
设发送码组为A=(a n-1，a n-2，…，a 1，a 0)，接收码组为R=(r n-1，r n-2，…，r 1，r 0)，由于发送码组A在传输中可能出现误码，因此接收码组R不一定与发送码组A相同。接收码组R与发送码组A之差为差错码组
其中，
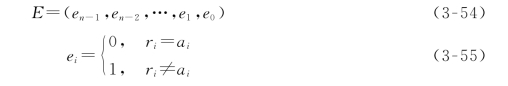
差错图样是指式(3-54)中差错码组的各种具体取样的图样。只有当差错图样与上述余式存在一一对应关系，才可能从余式唯一地决定差错图样，从而纠正错码。因此，原则上纠错可按下述步骤进行:
(a)用生成多项式g(x)除接收码组多项式R(x)=A(x)+E(x)，得出余式r′(x)。
(b)根据余式r′(x)用查表的方法或通过某种运算得到差错图样E。例如，通过计算校正子S和利用类似表3-4的关系，就可确定错码的位置。
(c)从R(x)中减去E(x)，便得到已纠正差错的原发送码组A(x)。
上述第一步运算和检错解码时的相同，第三步也很简单。只是第二步可能需要较复杂的设备，并且在计算余式和决定E(x)的时候需要把整个接收码组R(x)暂时存储起来。第二步要求的计算，对于纠正突发差错或单个差错的编码还算简单，但对于纠正多个随机差错的编码却是十分复杂的。
通过前面介绍过的表3-6的(7，3)循环码，可以看出，其码距为4，因此它有纠正1个差错的能力。这里，我们以此码为例给出一种硬件实现的纠错解码器的原理方框图，如图3-9所示。
图中上部为一个4级反馈移位寄存器组成的除法电路，它和图3-6中编码器的组成基本一样。接收到的码组，除了送入此除法电路外，同时还送入一缓冲寄存器暂存。假定现在接收码组为1000101，其中左边第2位为错码。此码组进入除法电路后，移位寄存器各级的状态变化过程列于表3-8中。当此码组的7个码元全部进入除法电路后，移位寄存器的各级状态自右向左依次为0100。其中移位寄存器c的状态为“1”，它表示接收码组中第2位有错(接收码组无错时，移位寄存器中状态应为全“0”，即表示接收码组可被生成多项式整除)。在此时刻以后，输入端使其不再进入信码，即保持输入为“0”，而将缓冲寄存器中暂存的信码开始逐位移出。在信码第2位(错码)输出时刻，反馈移位寄存器的状态(自右向左)为1000。“与门”输入为abcd，故仅当反馈移位寄存器状态为1000时，“与门”输出为“1”。输出“1”有两个功用:一是与缓冲寄存器输出的有错信码模2相加，从而纠正错码;二是与反馈移位寄存器d级输出模2相加，达到清除各级反馈移位寄存器的目的。
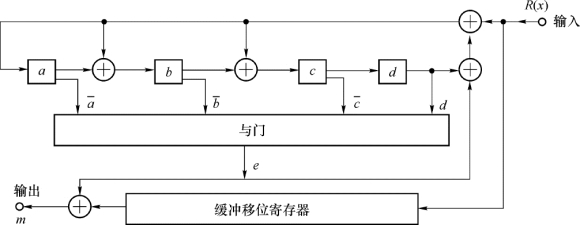
图3-9 解码器的原理方框图
表3-8 移位寄存器各级的状态变化过程
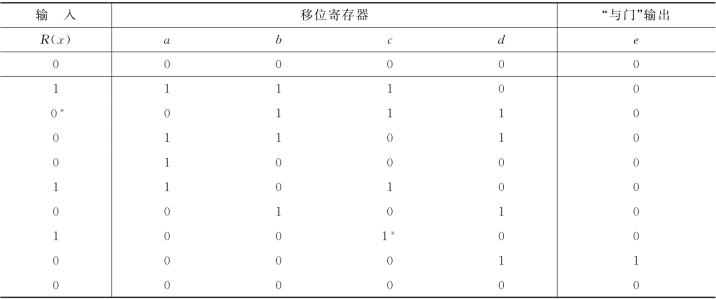
注:*表示错码位。
在实际应用中，一般情况下码组不是孤立传输的，而是一组组连续传输的。但是，由以上解码过程可知，除法电路在一个码组的时间内运算求出余式后，尚需在下一个码组时间中进行纠错。因此，实际的解码器需要两套除法电路(和“与门”电路等)配合一个缓冲寄存器，这两套除法电路由开关控制交替接收码组。此外，在解码器输出端也需有开关控制只输出信息位，删除监督位。这些开关图中均未示出。目前，解码器一般采用微处理器或数据信号处理器实现。
上述解码方法称为捕错解码法。通常，一种编码可以有几种纠错解码法。对于循环码来说，除了采用捕错解码、多数逻辑解码等方法外，其判决方法有所谓硬判决解码与软判决解码。在这里，只举例说明了捕错解码方法的解码过程，使我们看到错码是可以自动纠正以及是如何自动纠正的。
在数据通信中广泛采用的循环冗余检验(Cyclic Redundary Checks，CRC)简称CRC校验，循环冗余检验码简称CRC码。在常用的CRC生成器协议中采用的标准生成多项式如表3-9所示，数字12、16是指CRC余数的长度。对应地，CRC除数分别是13、17位长。
表3-9 常用的CRC码
