3.1.2 差错控制的基本原理
1.差错控制的原理
前面介绍了差错控制的基本思路,那为什么加了监督码后,码组就具有检错和纠错能力了呢?
下面举例说明这个问题。
例如,要传送A和B两个消息,可以用“0”码来代表A,用“1”码来代表B。在这种情况下,若传输中产生错码,即“0”错成“1”,或“1”误为“0”,接收端都无从发现,因此这种情况没有检错和纠错能力。
如果分别在“0”和“l”后面附加1个“0”和“1”,变为“00”和“11”,即“00”表示A,“11”表示B。这时,在传输“00”和“11”时,若发生1位错码,则接收端收到“01”或“10”,译码器将可判决为有错,因为没有规定使用“01”或“10”码组。这表明附加1位码(称为监督码)以后码组具有了检出1位错码的能力。但因译码器不能判决哪位是错码,所以不能予以纠正,这表明没有纠正错码的能力。本例中“01”和“10”称为禁用码组,而“00”和“11”称为许用码组。
进一步,若在信息码之后附加2位监督码,即用“000”代表消息A,用“111”表示B,这时,码组成为长度为3的二进制码,而3位的二进制码有23=8种组合,本例中选择“000”和“111”为许用码组。此时,如果传输中产生1位错码,接收端将收到“001”或“010”或“100”或“011”或“101”或“110”,这些(余下的6组)均为禁用码组,因此接收端可以判决传输有错。不仅如此,接收端还可以根据“大数”法则来纠正1个差错,即3位码组中如有2个或3个“0”码判为“000”码组(消息A),如有2个或3个“1”码判为“111”码(消息B),所以此时还可以纠正1位错码。如果在传输中产生2位错码,也将变为上述的禁用码组,译码器仍可以判为有错。
归纳起来,若要传送A和B两个消息:若用1位码表示,则没有检错和纠错能力;若用2位码表示(加1位监督码),则可以检错1位;若用3位码表示(加2位监督码),则最多可以检错2位或纠错1位。
由此可见,纠错编码之所以具有检错和纠错能力,是因为在信息码之外附加了监督码,即码的检错和纠错能力是用信息量的冗余度来换取的。监督码不载荷信息,它的作用是用来监督信息码在传输中有无差错,对用户来说是多余的,最终也不传送给用户,它提高了传输的可靠性。但是,监督码的加入,降低了信息传输效率。一般说来,加入监督码越多,码的检错、纠错能力越强,但信息传输效率下降也越多。
在纠错编码中,信息传输效率也称为编码效率,定义为
![]()
显然,R越大编码效率越高,它是衡量码性能的一个重要参数。对于一个好的编码方案,不但希望它的抗干扰能力高(即检错纠错能力强),而且还希望它的编码效率高,但这两个方面的要求是矛盾的,在设计中要全面考虑。人们研究的目标是寻找一种编码方法使所加的监督码元最少,而检错、纠错能力又高,且便于实现。
2.汉明距离与检错和纠错能力的关系
(1)几个概念
在信道编码中,定义码组中非零码元的数目为码组的重量,简称码重。例如,“010”码组的码重为1,“011”码组的码重为2。把两个码组中对应码位上具有不同二进制码元的个数定义为两个码组的距离,简称码距;而在一种编码中,任意两个许用码组间距离的最小值,称为这一编码的汉明(Hamming)距离,以d min表示。
(2)汉明距离与检错和纠错能力的关系
为了说明汉明距离与检错和纠错能力的关系,把3位码元构成的8个码组用一个三维立方体来表示,如图3-3所示。图中立方体的各顶点分别为8个码组,3位码元依次表示为A 1,A 2,A 3轴的坐标。
在这个3位码组例子中,若8种码组都作为许用码组时,任两组码间的最小距离为1,即这种编码的最小码距为d min=1;若只选用最小码距d min=2的码组,则有4种码组为许用码组;若只选用d min=3的码组,则有2种码组为许用码组。由图3-3可以看到,码距就是从一个顶点沿立方体各边移动到另一个顶点所经过的最少边数。图中粗线表示“000”与“111”之间的最短路径。
下面我们将具体讨论一种编码的最小码距(汉明距离)d min与这种编码的检错和纠错能力的数量关系。在一般情况下,对于分组码有以下结论。
(a)为检测e个错码,要求最小码距为
![]()
或者说,若一种编码的最小距离为d min,则它能检出e≤d min-1个错码。
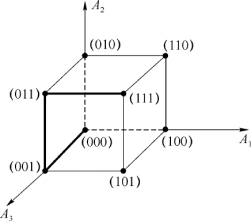
图3-3 码距的几何解释
式(3-2)可以通过图3-4(a)来证明。图中c表示某码组,当错码不超过e个时,该码组的位置将不超过以c为圆心以e为半径的圆(实际上是多维的球)。只要其他任何许用码组都不落入此圆内,则c码组发生e个错码时就不可能与其他许用码组相混。这就证明了其他许用码组必须位于以c为圆心,以e+1为半径的圆上或圆外,所以该码的最小码距d min为e+1。
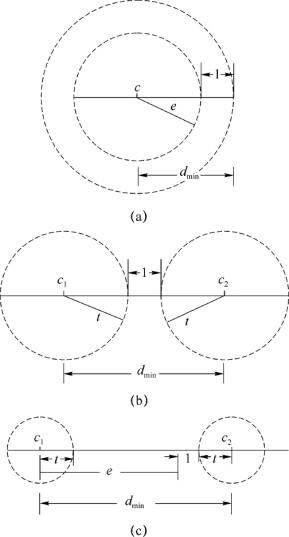
图3-4 汉明距离与检错和纠错能力的关系(https://www.daowen.com)
(b)为纠正t个错码,要求最小码距为

式(3-3)可以用图3-4(b)来说明。图中c 1和c 2分别表示任意两个许用码组,当各自错码不超过t个时,发生错码后两个许用码组的位置移动将分别不会超过以c 1和c 2为圆心,以t为半径的圆。只要这两个圆不相交,则当错码小于t个时,可以根据它们落在哪个圆内就能判断为c 1或c 2码组,即可以纠正差错。而以c 1和c 2为圆心的两个圆不相交的最近圆心距离为2t+1,这就是纠正t个错码的最小码距了。
(c)为纠正t个错码,同时检测e(e>t)个错码,要求最小码距为
![]()
在解释此式之前,先来说明什么是“纠正t个错码,同时检测e个错码”(简称纠检结合)。在某些情况下,要求对于出现较频繁但错码数很少的码组,按前向纠错方式工作,以节省反馈重发时间;同时又希望对一些错码数较多的码组,在超过该码的纠错能力后,能自动按检错重发方式工作,以降低系统的总误码率,这种方式就是“纠检结合”。
在上述“纠检结合”系统中,差错控制设备按照接收码组与许用码组的距离自动改变工作方式。若接收码组与某一许用码组间的距离在纠错能力t范围内,则将按纠错方式工作;若与任何许用码组间的距离都超过t,则按检错方式工作。
我们可以用图3-4(c)来证实式(3-4)。图中c 1和c 2分别为两个许用码组,在最不利情况下,c 1发生e个错码,而c 2发生t个错码,为了保证这时两个码组仍不发生相混,则要求以c 1为圆心、e为半径的圆必须与以c 2为圆心、t为半径的圆不发生交叠,即要求最小码距d min≥e+t+1。同时,还可以看到若错码超过t个,两圆有可能相交,因而不再有纠错的能力,但仍可检测e个错码。
在讨论了差错控制编码的纠错检错能力之后,现在转过来简要分析一下采用差错控制编码的效用,以便使读者有一些数量的概念。
设在随机信道中发送“0”时的差错概率和发送“1”的差错概率相等,均为P e,且P e≪1,则容易证明,在码长为n的码组中恰好发生r个错码的概率为
![]()
例如,当码长n=7时,P e=10-3,则有
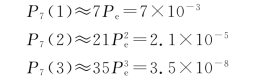
可见,采用差错控制编码后,即使只能纠正(或检测)这种码组中1~2个差错,也可以使误码率下降几个数量级。这就表明,就算是较简单的差错控制编码也具有较大实际应用价值。当然,如在突发信道中传输,由于错码是成串集中出现的,所以上述只能纠正码组中1~2个错码的编码,其效用就不像在随机信道中那样显著了,需要采用更为有效的纠错编码。
3.差错控制编码的分类
从不同的角度出发,差错控制编码可有不同的分类方法。
(a)按照码组的功能分,差错控制编码可分为检错码和纠错码两类。一般地说,能在译码器中发现差错的,称为检错码,它没有自动纠正差错的能力。既能在译码器中发现差错,又能自动纠正差错的,则称为纠错码,纠错码是最重要的一种抗干扰码。
(b)按照码组中监督码元与信息码元之间的关系分,差错控制编码可分为线性码和非线性码两类。线性码是指监督码元与信息码元之间呈线性关系,即可用一组线性代数方程联系起来,几乎所有得到实际运用的都是线性码;非线性码指的是监督码元与信息码元之间呈非线性关系,非线性码实现起来比较困难。
(c)按照信息码元与监督码元的约束关系分,差错控制编码可分为分组码和卷积码两类。所谓分组码是将k个信息码元划分为一组,然后由这k个码元按照一定的规则产生r个监督码元,从而组成长度n=k+r的码组。在分组码中,监督码元仅监督本码组中的码元,或者说监督码元仅与本码组的信息码元有关。分组码一般用符号(n,k)表示,并且将分组码的结构规定为图3-5所示的形式,图中前面k位(a n-1,a n-2,…,ar)为信息位,后面附加r个监督位(ar-1,ar-2,…,a 0)。
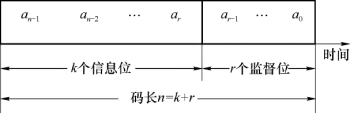
图3-5 分组码的结构
在卷积码中,每组的监督码元不但与本组码的信息码元有关,而且还与前面若干组信息码元有关,即不是分组监督,而是每个监督码元对它的前后码元都实行监督,前后相连,因此有时也称为连环码。
(d)按照信息码元在编码前后是否保持原来的形式不变,差错控制编码可分为系统码和非系统码。系统码中信息码元不改变原来的信号形式,而非系统码中信息码元则改变了原来的信号形式。由于非系统码中的信息位改变了原有的信号形式,这给观察和译码都带来了麻烦,因此很少应用,而系统码的编码和译码相对比较简单,所以得到广泛应用。
(e)按照纠正差错的类型分,差错控制编码可分为纠正随机差错的码和纠正突发差错的码。
(f)按照每个码元取值分,差错控制编码可分为二进制码与多进制码。
