3.4.2 循环码的生成多项式和生成矩阵
1.生成多项式g(x)
由前述已知,对于线性分组码,有了典型的生成矩阵G,就可以由k个信息码得出整个码组。如果知道监督方程,便可得到监督矩阵H,而由监督矩阵H和生成矩阵G之间的关系则可以求出生成矩阵G。这里介绍求生成矩阵G的另一种方法,即根据循环码的基本性质来找出它的生成矩阵。
由于G的各行本身就是一个码组,如果能找到k个线性无关的码组,就能构成生成矩阵G。
如何来寻找这k个码组呢?
一个(n,k)循环码共有2k个码组,其中有一个码组前k-1位码元均为“0”,第k位码元和第n位(最后一位)码元必须为“1”,其他码元不限制(既可以是“0”,也可以是“1”)。此码组可以表示为
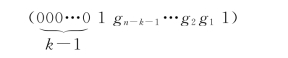
第k位码元和第n位码元之所以必须为“1”的原因是:
·在(n,k)循环码中除全“0”码组外,连“0”的长度最多只能有k-1位,否则,在经过若干次循环移位后将得到一个k位信息位全为“0”,但监督位不全为“0”的码组,这在线性码中显然是不可能的(信息位全为“0”,监督位也必定全为“0”)。
·若第n位码元不为“1”,该码组(前k-1位码元均为“0”)循环右移后将成为前k位信息位都是“0”、而后面n-k监督位不都为“0”的码组,这是不允许的。
以上证明(000…0 1 g n-k-1…g 2g 11)为(n,k)循环码的一个许用码组,其对应的多项式为
![]()
根据循环码的循环特性及式(3-35),xg(x),x 2g(x),…,x k-1g(x)所对应的码组都是(n,k)循环码的一个许用码组,连同g(x)对应的码组共构成k个许用码组。这k个许用码组便可构成生成矩阵G,所以我们将g(x)称为生成多项式。
归纳起来,(n,k)循环码的2k个码组中,有一个码组前k-1位码元均为“0”,第k位码元为“1”,第n位(最后一位)码元为“1”,此码组对应的多项式即为生成多项式g(x),其最高幂次为x n-k。
例3-5 求表3-6所示(7,3)循环码的生成多项式。
解 表3-6所示(7,3)循环码对应生成多项式的码组为第2个码组0010111,生成多项式为
g(x)=x 4+x 2+x+1
2.生成矩阵G
由循环码的生成多项式g(x)可得到生成矩阵G(x),为
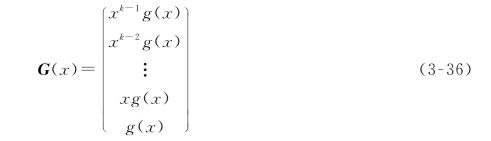
生成矩阵G(x)的每一行都是一个多项式,我们将每一行写出对应的码组则得到生成矩阵G,这样求得的生成矩阵一般不是典型的生成矩阵,要将其转换为典型的生成矩阵。典型的生成矩阵为
G=[I kQ]
可以通过线性变换将非典型的生成矩阵转换为典型的生成矩阵,具体方法是:任意几行模2加取代某一行,下面举例说明。
例如,我们要求表3-6所给的(7,3)循环码的典型的G。
首先求其生成多项式,上例已求出表3-6所给的(7,3)循环码的生成多项式,为
g(x)=x 4+x 2+x+1
根据式(3-36)得到生成矩阵G(x),为
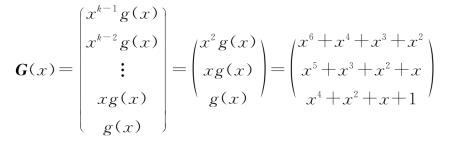 (https://www.daowen.com)
(https://www.daowen.com)
每一行写出对应的码组可得生成矩阵G,为

这个生成矩阵G是非典型的,要将其转换为典型的生成矩阵。根据观察,第1行⊕第3行取代第1行,则得到
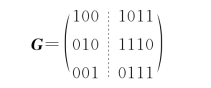
此生成矩阵G虚线前是一个3行3列的单位方阵,所以它是典型的生成矩阵。
将3位信息码a 6a 5a 4(000,001,010,011,…,111)与典型的生成矩阵G相乘便可得到全部码组,即表3-6所示。
3.生成多项式g(x)的另一种求法
利用式(3-27),我们可以写出表3-6循环码组所对应的多项式,即
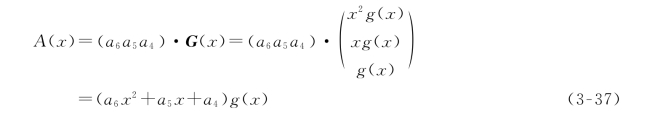
由此可见,任一循环码的多项式A(x)都是g(x)的倍数,即都可被g(x)整除,而且任一幂次不大于k-1的多项式乘g(x)都是码的多项式。
这样,循环码组的A(x)也可写成
![]()
其中,h(x)是幂次不大于k-1的多项式。
已知生成多项式g(x)本身就对应循环码的一个码组,令
![]()
因为A g(x)是一个n-k次多项式,所以x kA g(x)为一个n次多项式。由式(3-34)可知,在模x n+1运算下也是一个许用码组(即它的余式为一许用码组),故可以写成
![]()
式(3-40)左边的分子和分母都是n次多项式,所以其商式Q(x)=1,这样,式(3-40)可简化成
![]()
将式(3-38)和式(3-39)代入式(3-41),并化简后可得
![]()
式(3-42)表明,生成多项式g(x)必定是x n+1的一个因式。这一结论为我们寻找循环码的生成多项式指出了一条道路,即循环码的生成多项式应该是x n+1的一个n-k次因子。
例如,x 7+1可以分解为
![]()
为了求出(7,3)循环码的生成多项式g(x),就要从式(3-43)中找到一个n-k=7-3=4次的因式。从式(3-43)不难看出,这样的因式有两个,即
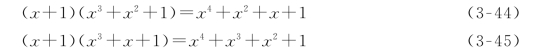
式(3-44)和式(3-45)都可以作为(7,3)循环码的生成多项式g(x)用。不过,选用的生成多项式不同,产生出的循环码码组也不同,用式(3-44)作为生成多项式产生的(7,3)循环码即为表3-6所列。
