2.2.4 数据序列的扰乱与解扰
1.扰乱与解扰的作用
在前面的讨论中，我们都假定数据序列是随机的，但是会有一些特殊情况，例如一段时间的连“0”或连“1”和一些短周期的确定性数据序列等。这样的数据信号对传输系统是不利的，主要是由于:
·可能产生交调串音。短周期或长“0”、长“1”序列具有很强的单频分量，这些单频可能与载波或已调信号产生交调，会对相邻信道的数据信号产生干扰。
·可能造成传输系统失步。长“0”或长“1”序列可能造成接收端提取定时信息困难，不能保证系统具有稳定的定时信号。
·可能造成均衡器调节信息丢失。时域均衡器调节加权系数需要数据信号具有足够的随机性，否则可能导致均衡器中的滤波器发散而不能正常工作。
综上所述，要使数据传输系统正常工作，需要保证输入数据序列的随机性。为了做到这一点，可以在数据传输系统的发送端对输入数据序列进行扰乱。
所谓扰乱，就是将输入数据序列按某种规律变换成长周期序列，使之具有足够的随机性。经过扰乱的数据序列通过系统传输后，在接收端再还原成原始的数据序列，即为解扰。
2.扰乱和解扰的基本原理
最有效的数据序列扰乱方法是用一个随机序列与输入数据序列进行逻辑加，这样就能把任何输入数据序列变换为随机序列。扰乱器与解扰器原理如图2-17所示。
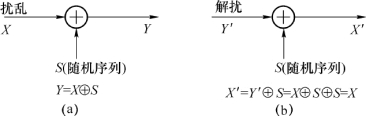
图2-17 扰乱器与解扰器原理图
如图2-17(a)所示输入序列X与随机序列S进行模2加处理后即可得扰乱序列Y，这时的Y就具有完全的随机性。接收端的解扰如图2-17(b)所示，将接收到的已扰序列与随机序列S进行模2加，即可恢复原始数据序列。
为了解扰，必须在接收端产生一个与发送端完全一致的，并在时间上同步的随机序列。实际上，完全随机的序列是不能再现的，因此一般用伪随机序列来代替完全随机序列进行扰乱与解扰。
3.自同步扰乱器和解扰器
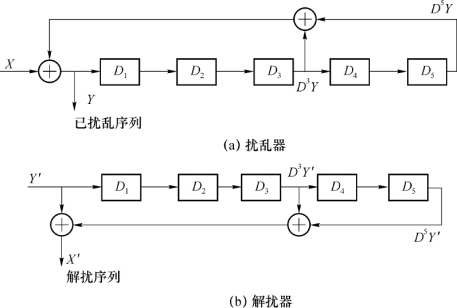
图2-18(a)给出一个由5级移位存储器组成的扰乱器原理图，图2-18(b)为相应的解扰器。图中经过一次移位，在时间上延迟一个码元时间，用运算符号D表示。
图2-18 自同步扰乱器与解扰器
设X和Y分别表示扰乱器的输入和输出序列，X′和Y′分别表示解扰器的输入和输出序列，则如图2-18所示逻辑关系，可有
发送端
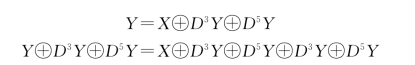
因为序列自身的模2加为0，所以有
接收端
无误码时Y=Y′，则由式(2-26)得
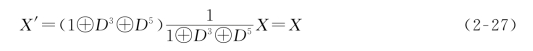
例2-3 如数据序列为1010101010 0000000000，求该序列通过图2-18所示扰乱器的输出序列。
解 将式(2-26)进行展开得
由于DnX只是将X序列延迟n个码元，所以将上式中各项对应的序列排列如下:
从上式可以看出，比D 20X更大的幂次，其延迟已经超出输入的码位数，可以不计。此时的已扰序列Y消除了短周期和长连“0”(也适用于长连“1”)。