3.5.3　卷积码的概率解码

前面提到过，卷积码的解码方法一般有两类:代数解码和概率解码。有关代数解码已经做过介绍，如图3-13所示。

这里讨论概率解码，我们知道它要利用信道的统计性质进行解码。

在卷积码的概率解码中，有一类称为最大似然算法，其思路是:把接收序列与所有可能的发送序列(相当于网格图中的所有路径)相比较，选择一种码距最小的序列作为发送序列。在这一思路下，若发送一个k位序列，则有2k种可能序列，计算机应存储这些序列，以便用作比较。因此，当k较大时，存储量和计算量太大，受到限制。1967年维特比(Viterbi)对最大似然解码作了简化，称为维特比算法(简称VB算法)。VB算法不是一次比较网格图上所有可能的序列(路径)，而是根据网格图每接收一段就计算一段，比较一段后挑出并存储码距小的路径，最后选择出的那条路径就是具有最大似然函数(或最小码距)的路径，即为解码器的输出序列。

我们用一个例子来说明VB算法的概念。当发送序列为11010时，为了使全部信息位能通过编码器，在发送序列后加上3个“0”，使输入编码器序列变为11010000。经过卷积编码，编码器输出序列为1101010010110000，如表3-10所示。假设接收序列有差错，序列变成0101011010010001。现在我们对照图3-16的网格图来介绍VB的解码过程，如图3-19所示。

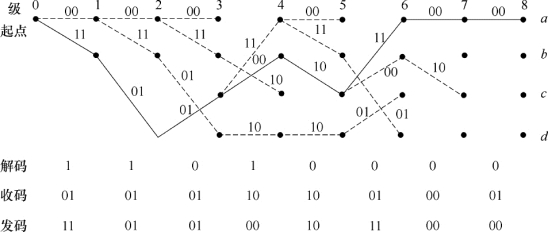
图3-19　VB解码图解举例

在本例中，编码约束长度n N=2×3=6，可以前3段6位码的接收序列010101作为计算的标准。若把网格图的起点作为0级，则6位码正好到达第三级的4个节点(状态)，从网格图上可知从0级起点到第三级的4个节点一共有8条路径。到达第三级节点a的路径有两条:000000与111000。它们和010101之间的码距分别是3和5，其中码距较小的路径称为幸存路径，保留下来。同理，到达第三级节点b，c，d的路径中，各选一条幸存路径，分别为000000，000011，110101和001101，它们与010101的对应码距分别是3，3，1和2。从第三级再推进到第四级也同样有8条路径(参见图3-16)，例如到达第四级节点a的两条路径为00000000和11010111，与接收序列01010110的码距为4和2，把路径11010111作为幸存路径，同理，到达第四级的b，c，d的幸存路径为11010100，00001110和00110110，逐步按级依次选择幸存路径。由于本例中，要求发送端在发送信息序列后面加上3个“0”，因此最后路径必然终结于a状态(见表3-10)。这样，在到达第七级时只要选出节点a和c的两条路径即可，因为到达终点a只可能从第七级的节点a或c出发。在比较码距后，得到一条通向终点a的幸存路径，即解码路径，如图中实线所示。再对照图3-16中的实线表示“0”码，虚线表示“1”码，可确定每段解码幸存路径所对应的码元是“1”或是“0”，即得到解码码元，如图中的11010000，与发送信息序列一致。