2.2.2 基于Vaughan模型的二次电子发射特性模拟
20世纪40年代末,研究人员通过观察二次电子发射测量实验,发现了在不同入射角度下的SEY曲线变化趋势,并提出了SEY曲线关键参数Emax和δmax(图1-6)随入射角度θin的变化趋势[3-4]:
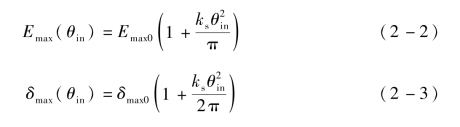
式中,Emax0——垂直入射时最大SEY对应的入射电子能量,eV;
ks——材料表面平滑因子;
δmax0——垂直入射时最大SEY。
20世纪50年代末,Lye等[5]在充分收集多种材料的二次电子发射特性测量数据,并对SEE数据进行分析的基础上,基于指数函数假设初步提出了SEY曲线拟合模型:
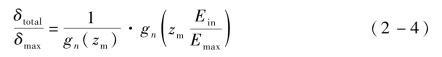
式中,Ein——入射电子能量,eV;
zm——函数gn(z)达到最小值时z的取值;
n——曲线拟合系数;
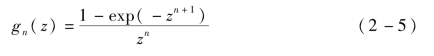
选取不同的n,可对不同能量段实现不同的拟合精度。同时,选取不同的n的具体值能够对式(2-5)进行简化。
受限于二次电子测量设备和测量系统的准确性,以上二次电子发射模型并未得到广泛应用。直到20世纪80年代末,二次电子发射测量仪器与实验科学得到较大发展,科学界对于材料表面科学中的二次电子发射现象有了新的认识。美国学者Vaughan提出了基于曲线的SEY模型,并经过部分实验数据的验证,通常将Vaughan提出的二次电子产额模型定义为Vaughan模型。与基于经验和推算的公式相比,Vaughan模型更为准确地描述了不同材料的SEY曲线,尤其是不同入射角度下的SEY曲线。同时,Vaughan模型对于较低能量段的SEY拟合较为准确,适用于对低能量段二次电子发射进行研究的应用场合。而且,Vaughan模型并不依赖于材料,仅对SEY曲线从数学上进行拟合和描述,不考虑实际发射过程中的物理效应。
在图1-6所示的典型SEY曲线中,对微放电效应影响最大的参数有:第一能量点E1、第二能量点E2、SEY最大值δmax、δmax对应的入射电子能量Emax。当电子雪崩倍增引发微放电效应时,每次碰撞出射的二次电子数目平均值应当大于1。因此E1和E2之间的SEY将对电子出射和微放电阈值功率产生明显影响。Vaughan模型考虑了SEY曲线上几个关键特征参数,提出了垂直入射条件下SEY曲线的数学拟合方程:
![]()
其中,
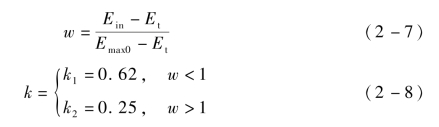
式中,Et——阈值能量,eV。
当入射电子能量低于Et时,Vaughan模型不再适用。
基于当时的实验研究条件,Vaughan模型中定义Et为12.5 eV。这是由于低能二次电子发射的测量与表征非常复杂,同时受到地磁场和环境影响,微弱的变化将导致较大的误差。因此,Vaughan模型中不考虑极低入射能量时的SEY。换言之,当入射电子能量低于12.5 eV时,Vaughan模型不再有效。一般而言,不考虑入射能量小于20 eV时的二次电子发射。当w=1时,式(2-6)为确定值,k的取值可为任意值。为了平衡w<1和w>1之间的不连续性,可定义k为
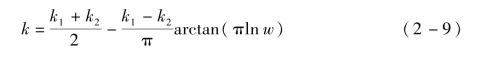
通过测量确定k1和k2:
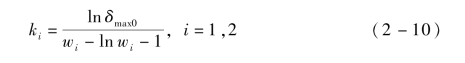
式中,

当定义垂直于材料表面的入射角度为0°时,SEY随着入射角度的增大而呈现增大趋势。这是因为,当电子斜入射到材料表面时,电子进入材料的深度变小,能够释放更多的二次电子。随着电子垂直入射到材料表面,电子进入材料的深度变大,释放的二次电子较少。考虑角度的影响,结合式(2-6),将Vaughan模型修正为
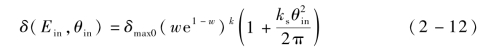
同时采用式(2-2)表示不同入射角度下的入射电子能量。值得注意的是,ks表征了材料表面的光滑程度。ks受表面粗糙度的影响,但与表面粗糙度并非同一参数,仅用于不同入射角度下的SEY曲线的拟合。对于采用传统机械加工工艺的材料表面,ks可取值为1。ks越大,表示表面越平滑;反之,则代表表面越粗糙。对于碳化表面或具有微结构的材料表面,ks甚至可能减小为0。此时,SEY曲线不再随入射电子角度变化。
对于微放电数值模拟,所采用的二次电子发射理论模型应当满足以下基本条件:
(1)完整描述全能量段的二次电子发射特性,包括二次电子发射产额、发射的二次电子能量分布(能谱)与角度分布。(https://www.daowen.com)
(2)能够描述低能端(0<Ein<E1)的二次电子发射特性。
基于以上要求,将Vaughan模型修正为
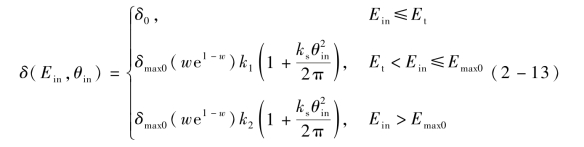
式中,δ0——当入射电子能量小于阈值能量Et时的二次电子产额。可直接在微放电数值模拟中进行预设(一般取值小于1),然后根据微放电数值模拟结果对δ0进行校验。
对于金属材料的二次电子发射特性模拟拟合,首先针对具体材料表面SEE特性进行实验研究,获得不同入射角度下的SEY测量曲线;然后,根据获得的SEY曲线直接获得δmax0和Emax0的值,通过拟合得到特征函数k1、k2和ks的值。对于δ0,可直接在微放电数值模拟中根据分析结果进行校验。若对SEY曲线的拟合精度有更高要求,可增加拟合参数ksE和ksθ,拟合不同入射角度下的入射电子能量和出射产额。若对更高能量段的拟合精度有更高要求(如Ein>3Emax0),可将式(2-13)进一步修正,得到不同能量段的k3和k2,3等。
应用修正Vaughan模型时,为了满足微放电数值模拟对二次电子发射模拟的完整性,采用麦克斯韦分布模拟二次电子能量分布:
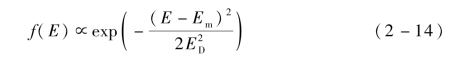
式中,Em——二次电子平均出射能量,eV;
ED——二次电子出射能量的均方根,eV。
采用余弦分布模拟出射二次电子的角度分布:
![]()
式中,θ∈[0°,90°],定义电子垂直于材料表面出射时的θ为0°。
接下来,以采用机械加工工艺制备的铝合金镀银和铝合金材料为例,说明采用Vaughan模型对实验测得SEY曲线进行拟合的过程。
如图2-3所示,加工尺寸为10 mm×20 mm×1 mm的镀银样片。镀银样片的基片材料为铝合金,镀银厚度约为10 μm。铝合金镀银样片的实物图如图2-3(a)所示,样片表面的SEM(scanning electron microscope,扫描电子显微镜)图像如图2-3(b)所示,均匀光滑、致密度高。

图2-3 铝合金镀银样片
(a)实物图;(b)SEM图像
采用离子清洗前和清洗后的铝合金镀银样片的SEY测量曲线如图2-4所示。采用离子枪对样片进行清洗,清洗时间为10 min。
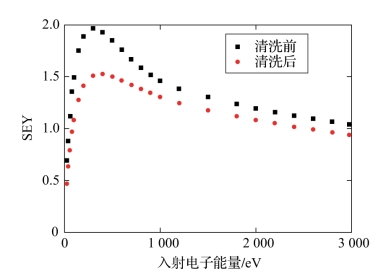
图2-4 采用离子清洗前和清洗后的铝合金镀银样片的SEY测量曲线(附彩图)
针对未清洗的铝合金镀银样片,测量得到不同入射角度下SEY曲线,如图2-5所示。从SEY曲线中提取得到δmax0为2.0,Emax0为200 eV。结合不同入射角度下的SEY曲线,采用数值拟合方法获得Vaughan模型的关键参数k1、k2和ks的值,如表2-1所示。
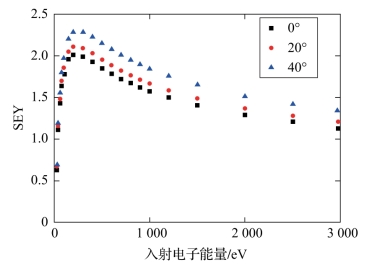
图2-5 不同入射角度下未清洗的铝合金镀银样片的SEY测量曲线(附彩图)
表2-1 Vaughan模型拟合参数

针对采用离子清洗后的铝合金样片,测量得到不同入射角度下SEY曲线,如图2-6所示。从SEY曲线中提取得到δmax0为1.48,Emax0为500 eV。采用数值拟合方法获得Vaughan模型的关键参数k1、k2和ks的值,如表2-1所示。
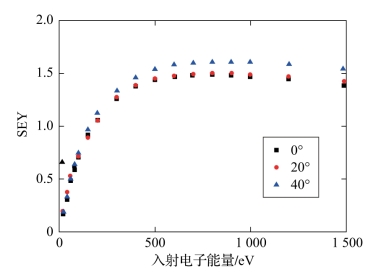
图2-6 不同入射角度下采用离子清洗后的铝合金样片SEY测量曲线(附彩图)
采用表2-1中根据实验测试结果提取得到的关键拟合参数建立Vaughan模型,得到的SEY曲线拟合结果如图2-7和图2-8所示。
观察可知,针对未清洗的镀银样片和采用离子清洗后的铝合金样片,采用Vaughan模型获得了较好的拟合结果,拟合误差较小。同时,在入射角度θin≤40°时,可获得较好的拟合精度。当电子入射角度θin>40°时,受电子散射效应的影响,采用电流偏压法测量得到的SEY数据准确度与可重复度下降。
