7.4.4 微放电阈值分析仿真实例
针对铁氧体环行器微放电数值模拟,将仿真时间在时间域上离散成均匀时间步长Δt,将环行器模型及整体计算区域在空间域上离散成非均匀六面体网格,随时间步长推进计算,得到一定输入功率条件下铁氧体环行器电磁场分布以及粒子运动状态随时间的演变情况。根据不同的输入功率下计算区域中粒子(或二次粒子)数目随时间的变化趋势,判断铁氧体环行器发生微放电效应的阈值功率。
首先对传统金属微放电阈值功率的判定方法进行介绍。图7-18所示为工作于C频段(中心工作频率f0为3.8 GHz)的5阶阻抗变换器的对称结构在不同输入功率下计算得到的空间中总粒子数目随时间变化的趋势。
在数值模拟的初始化阶段,在阻抗变换器最窄间距处的真空区域均匀设置105个初始粒子。初始粒子的能量和角度分布如前所述。
当电磁场计算稳定后,粒子在电磁场的驱动下在微波部件内部以一定速度随机扩散,直至与边界发生碰撞,被吸收或者产生二次电子发射。在微放电尚未发生的起始阶段(通常小于数十个射频周期Trf,Trf=1/f0),大部分初始粒子被边界吸收,仅有在电磁场加速后具有一定能量且满足一定相位效应的粒子能与电磁场相位变化同步。将此现象定义为微放电电子谐振效应,且二次电子发射周期Ns与电磁场相位变化周期Nrf同步,Ns=niNrf,其中ni为每两次碰撞之间射频电磁场反向的次数,即微放电的阶数。
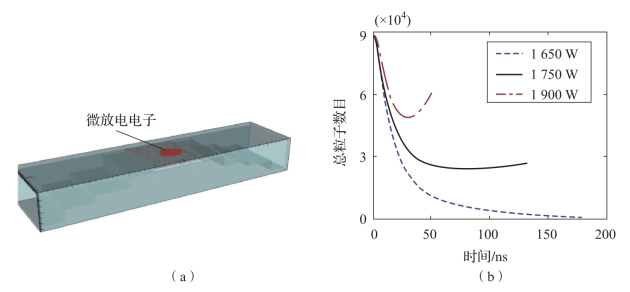
图7-18 5阶阻抗变换器(附彩图)
(a)对称结构的三维模型;(b)计算区域中总粒子数目随时间变化的趋势
对于不存在谐振的阻抗变换器,当输入功率低于1 650 W时,经历数个周期(通常远大于100个射频周期)的相位选择后,总粒子数目持续衰减,将不能建立起微放电过程。与此相反,当输入功率足够大(大于1 750 W)时,粒子数目将呈指数增长,这意味着将发生二次电子雪崩效应,最终导致微波部件中的微放电击穿。因此,根据计算空间中总粒子数目随时间的变化趋势,可以推断微放电阈值功率为1 750 W。值得注意的是,受限于每次仿真时采用的输入功率的步进步长,采用该方法推断得到的微放电阈值精度有限。例如在本例中,由于每次仿真输入功率的步进值为10 W,则仿真得到的微放电阈值功率精度为±10 W。
对于强谐振、具有强非规则结构(或微细结构)的微波部件(如滤波器),电磁场变化较为剧烈,计算空间中的初始粒子随时间的离散效应并不明显。在尚未积累足够多的二次电子、微放电效应尚未建立的起始阶段,在空间随机加载的初始粒子需要较长的时间才能使得不满足微放电谐振条件的粒子完全被边界吸收。在此过程中,若有部分粒子已经建立微放电谐振条件,发生固定周期的二次电子发射及倍增,则总粒子数目呈先上升后下降的趋势。此时,若微放电数值模拟时间不够长,就会发生微放电阈值的误判。
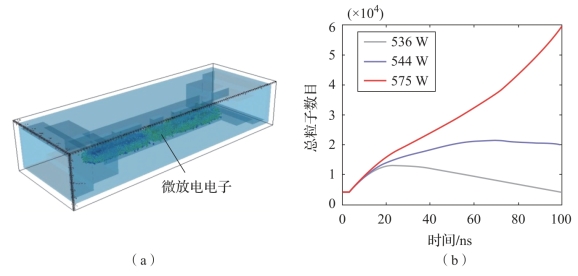
图7-19(a)所示为脊波导滤波器三维模型,微放电数值模拟频率为3.9 GHz,腔体金属材料为银。发生微放电时,电子在特定脊波导与腔体壁之间的空间聚集。显而易见的是,此时空间中其他脊波导处仍有初始粒子未被完全吸收。图7-19(b)所示为脊波导滤波器计算区域中总粒子数目随时间变化的趋势。当输入功率为536 W时,总粒子数目呈现先上升后缓慢下降的趋势。此时,若仿真时间不够长(≤100Trf),则出现对微放电阈值功率的误判,而实际上积累的粒子中一部分为初始粒子,一部分为初始粒子与边界碰撞后产生的不会发生倍增的二次电子,另一部分才是最后对二次电子倍增产生贡献的二次电子。其中,初始粒子与边界碰撞后产生的不会发生倍增的二次电子会随着数值模拟时间的增加而逐渐被边界吸收。
 (https://www.daowen.com)
(https://www.daowen.com)
图7-19 脊波导滤波器(附彩图)
(a)三维模型;(b)计算区域中总粒子数目随时间变化的趋势
基于以上研究与判断,本节针对具有强谐振或非均匀性的微波部件微放电阈值判定方法进行讨论,提出了一种基于平均SEY进行判定的方法。其基本思路为:在数值模拟过程中随时间步记录总粒子数,也记录产生的二次粒子数,然后进行数值滤波处理。由于银的最大SEY δmax0为2.2,即每次碰撞得到的SEY在0~3之间,随入射能量不同呈现较大的随机性分布,无法直接进行判断。此时,对二次电子数目进行均值滤波,将记录得到的每个时间步Δt时总的SEY按照每m个时间步求平均。对于最后m个时间步的总SEY,按照每(mmax-i)Δt求平均,其中mmax为仿真最大时间步,i为最后m个时间步中的第i个时间步。
由此,得到该脊波导滤波器在输入功率为536 W和544 W时的平均SEY随时间变化的趋势,如图7-20所示。显而易见,在滤除了初始粒子的影响后,根据平均SEY易于判断该输入功率下是否发生二次电子倍增效应。当输入功率为536 W时(图7-20(a)),平均SEY持续下降,不会发生微放电;当输入功率为544 W时(图7-20(b)),平均SEY随时间变化趋势几乎保持不变,SEY曲线斜率约为零,可判定此时的输入功率为微放电功率阈值。
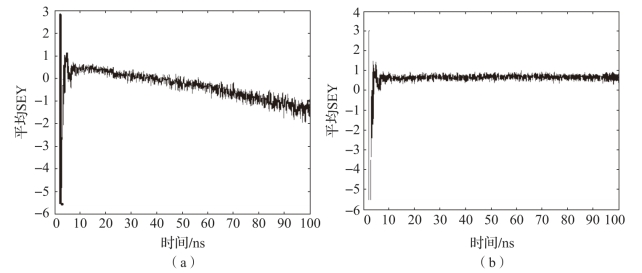
图7-20 不同输入功率下脊波导滤波器平均SEY随时间变化的趋势
(a)536 W;(b)544 W
得到总的二次电子数目作数值滤波的曲线(图7-19(b))后,进一步根据平均SEY曲线随时间变化趋势(图7-20)进行微放电阈值功率判断。
当输入功率一定时,在仿真时间达到100Trf后,取Np个时间步的平均SEY N1,然后取后Np个时间步的平均SEY N2。若N2>1.1N1,则认为发生微放电;若N1≤N2≤1.1N1,则认为该输入功率为微放电阈值功率;若N1>N2,则认为不发生微放电。
相比于基于总粒子数进行微放电阈值判定而言,该方法屏蔽了初始粒子及其随机分布的影响,准确度更高。
