2.4 金属表面形貌对微放电影响数值模拟研究
基于全波电磁计算方法与粒子模拟技术,对三维计算空间中微放电电子随时间演变规律与趋势进行追踪,能够实现大功率金属微波部件中微放电效应数值模拟与阈值分析。采用FDTD算法实现微波部件中三维电磁场分布计算。结合本章中表面形貌对材料SEE特性影响的实验和模型拟合研究,在微放电数值模拟EM-PIC算法中嵌入考虑表面形貌的SEE模型(图2-17),在本节中通过数值模拟研究材料表面形貌特性对微放电效应的影响。
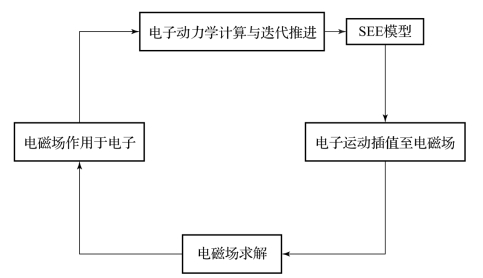
图2-17 材料表面形貌特性对微放电的影响仿真研究EM-PIC核心算法示意图
选择两种典型行波结构和强谐振结构微波部件进行数值模拟研究和仿真验证,包括金属矩形波导腔阻抗变换器和金属同轴腔体滤波器。如图2-18和图2-19所示,缺省单位为毫米(mm),微波部件结构材料为银。微放电数值模拟频率分别为3.85 GHz和0.45 GHz。
如表2-4和表2-5所示,当金属材料表面具有不同的表面随机粗糙度和非规则微孔隙等表面形貌时,二次电子发射特性呈现较大变化。表面形貌对SEE特性的影响主要体现在两方面。一方面,不同入射角度下全能量段的SEY均发生较大变化,此时定义为表面形貌对SEE的散射效应,在SEE模型中用ks表征。另一方面,表现为同一入射角度下SEY产额的明显差异,在SEE模型中表现为E1、δmax0和Emax0的变化。在微放电数值模拟中考虑不同形貌下相对应的SEE模型及其实验拟合结果,研究表面形貌对金属微波部件微放电阈值的影响。
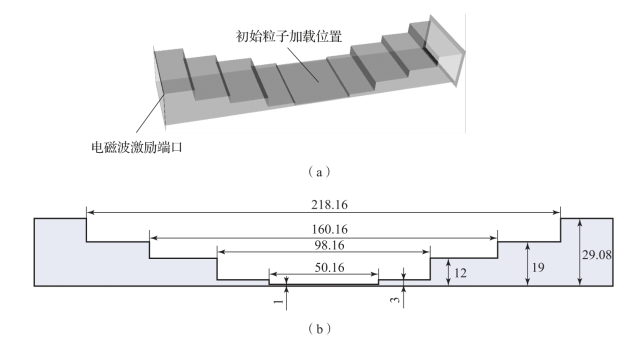
图2-18 阻抗变换器的对称结构
(a)三维结构;(b)物理尺寸
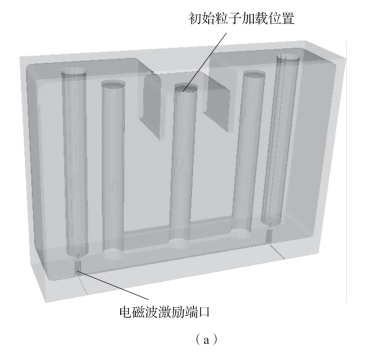
图2-19 同轴腔体滤波器
(a)三维结构
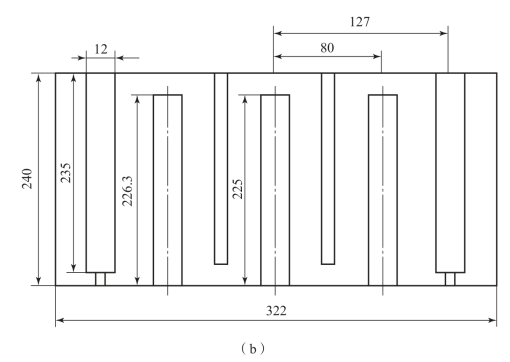
图2-19 同轴腔体滤波器(续)
(b)物理尺寸(单位:mm)
图2-20、图2-21给出了在微放电演变的不同阶段,不同的表面状态参数ks对粒子入射角度概率分布特性的影响。在微放电初始化阶段,粒子入射角度服从余弦分布。经过数百个射频周期的演变,在电磁场的作用下,考虑较大出射角度时电子的耗散,最终对微放电产生贡献的粒子入射角度集中在0°~30°,该过程几乎不受表面状态的影响。对于表面较为粗糙(ks=0.5)和较为光滑(ks=1.0)的状态,粒子入射角度分布概率呈现几乎相同的分布。
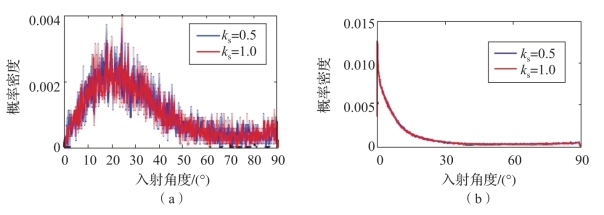
图2-20 金属阻抗变换器中不同表面状态下粒子入射角度概率密度分布(附彩图)
(a)初始化阶段;(b)发生微放电阶段
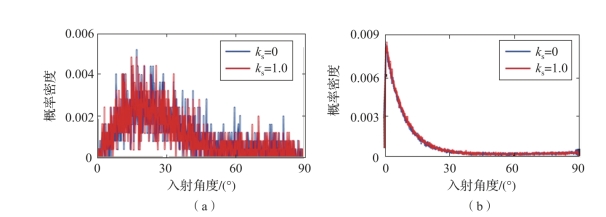
图2-21 金属同轴腔体滤波器中不同表面状态下粒子入射角度概率密度分布(附彩图)
(a)初始化阶段;(b)发生微放电阶段
图2-22显示了在发生微放电时,不同的表面状态参数ks对粒子入射能量概率分布的影响。当在微波部件中发生微放电时,二次电子在其渡越过程中从电磁场中获得几乎相等的能量。由于微放电发生时,粒子入射角度集中在0°~30°,因此粒子与金属表面碰撞能量几乎不受表面形貌对不同入射角度下二次电子散射效应的影响。值得注意的是,表面形貌的尺寸为微米(μm)量级,比物理尺寸为厘米(cm)量级的微波部件小数个数量级,无法直接建模分析。因此,通过在微放电数值模拟中结合SEE模型进行数值模拟和定性分析。在微结构中对电子运动的准确轨迹追踪和微观分析需要用到蒙特卡洛算法。
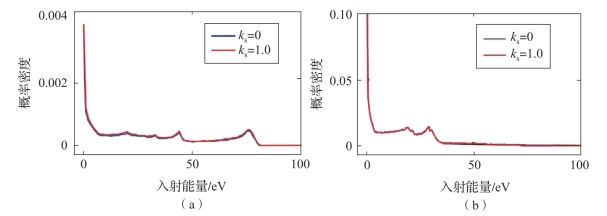
图2-22 不同表面状态下粒子入射能量概率密度分布(附彩图)
(a)阻抗变换器;(b)同轴腔体滤波器
图2-23显示了不同表面状态参数ks对微放电演变过程中二次电子数目和总粒子数目的影响。表面散射作用越强(即ks越小),则从表面出射的二次电子越少,计算空间中总粒子数目越少。但是,二次电子数目或总粒子数变化的范围在5%以内,对微放电阈值的影响可忽略。
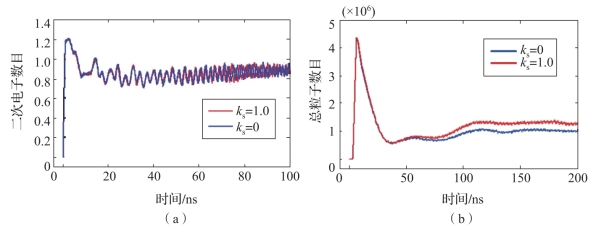
图2-23 不同表面状态下粒子数目随时间变化趋势(附彩图)
(a)阻抗变换器;(b)同轴腔体滤波器
表面状态除了对入射电子产生随角度变化的散射效应外,还对二次电子发射净产额产生影响,在SEE模型中体现为E1、δmax0和Emax0的变化。图2-24给出了不同的E1、δmax0和Emax0下微波部件微放电阈值的变化趋势。由数值模拟结果可知,E1是对微放电阈值影响最大的SEE参数,通常情况下大于δmax0和Emax0产生的影响。(https://www.daowen.com)
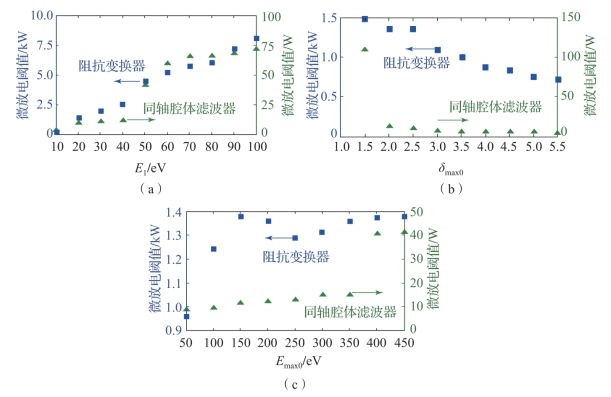
图2-24 金属微波部件中微放电阈值随二次电子发射特性参数的变化情况(附彩图)
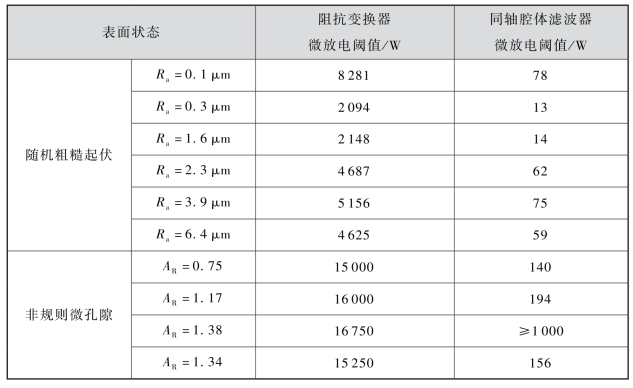
不同表面状态下的金属微波部件微放电阈值如表2-6所示。对于工程中常用的机械加工工艺,材料表面随机粗糙度Ra为0.3~1.6 μm,对微波部件微放电阈值的影响较小。当材料表面粗糙度较小(Ra<0.1 μm),接近理想光滑平面时,微放电阈值达到最大,为常用机械加工表面的3~4倍。对于机械加工具有随机粗糙度的材料表面,随着随机粗糙度的持续增加,微放电阈值有一定提高。对于具有一定深宽比的非规则微孔隙表面,金属微放电阈值大幅度提高。深宽比越大,微放电阈值越高。
表2-6 不同表面状态下的金属微波部件微放电阈值
当表面形貌的改变使得E1足够大时,金属微波部件中将不再发生微放电效应。以金属同轴腔体滤波器为例,微放电效应发生在滤波器内部最窄间距处,位于谐振柱的顶端与对应的腔体壁之间。微放电电子的运动受牛顿-洛伦兹方程驱动:

式中,v——电子的运动速度,m/s;
m——单位电子质量,kg;
e——单位电子电荷量,C;
E——电场矢量,V/m;
B——磁感应强度,T。
电子的渡越时间t0由微波部件最窄间距处的边界条件给定:

式中,d——微波部件最窄间距,m;
v⊥——电子运动速度v垂直于微波部件表面的分量,m/s。
假设电磁场激励为空间均匀分布的时谐场,则电场强度为
![]()
式中,E0——电场幅度,V/m;
ω0——电场角频率,rad/s。
假设电子入射时初始电场相位为α,初始速度为v0,此时以速度v0⊥发射,忽略磁场,则电子的碰撞速度为
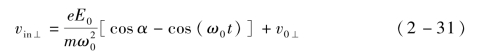
当微放电发生时,电子将在时间为T0时与出射位置对应的另一表面发生碰撞,且碰撞时间满足如下条件:
![]()
除了电磁场的谐振条件以外,电子垂直入射时的碰撞能量Ein⊥应大于第一能量点E1。由此,发生微放电的最大电子相位极限为
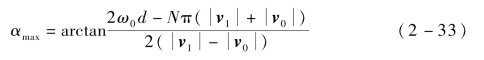
式中,v1——对应于E1的速度,m/s。
如果电子两次碰撞之间的距离过小,或者电磁场入射功率过高导致电子与微波部件碰撞时远未到达电磁场反向时间,将不会发生微放电效应。因此,不发生微放电效应的电子相位极限为
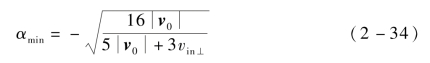
由此可推断,当材料表面状态的改变使得E1增大,导致αmin>αmax时,微波部件中将不会发生微放电。通过粒子模拟仿真验证,当E1≥200 eV时,金属同轴腔体滤波器不再发生微放电效应。不会发生金属微放电的E1极限值由具体器件的物理结构、电磁场分布和材料表面状态共同决定,需要通过数值求解。
