7.3 微放电电子运动轨迹等效模型研究
对于铁氧体环行器，由于存在介质表面电荷积累场、外加偏置磁场等，金属-金属双边微放电等效分析模型不再适用，基于高功率介质窗研究对象建立的单边微放电分析模型同样不再适用。针对大功率磁性部件微放电分析，基于物理原理抽象与等效近似，首先建立金属-介质双边微放电等效分析模型，如图7-7所示。其中，Erf为射频时变电场，Edc为介质表面电荷积累静态场，B0为外加偏置静磁场，d为金属-介质间距。
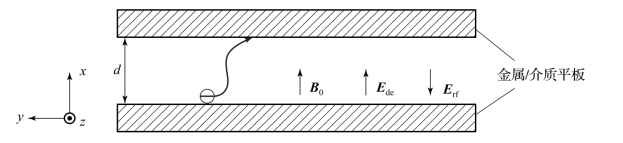
图7-7 双边微放电等效分析示意图
采用两个无限大平行平面物理模型与理想电磁场分布，考虑表面电荷积累、外部偏置场等因素的影响，忽略边缘场效应，在直角坐标系中建立双边微放电电子运动轨迹追踪等效分析模型。电子运动轨迹方程为
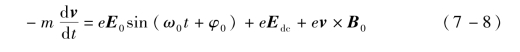
假设电磁场传输方向垂直于介质表面，则对于工作于TM模式的磁性介质微波部件而言，理想情况下的混合电磁场分布如图7-7所示。假设射频电场为
式中，E0——射频电场幅度，V/m；
φ0——射频电场初始相位，V/m。
此时，表面电荷积累场为
外部偏置磁场为
假设电子初始能量为Ee，发射角度与x轴的夹角为α、与y轴的夹角为β，则求解式（7-8）得到的电子运动速度分量分别为
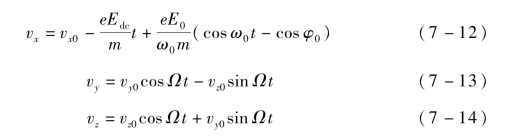
式中，
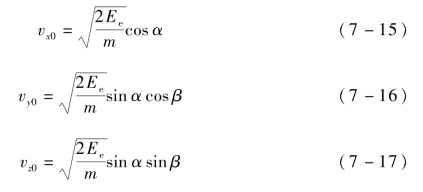
式中，Ω——磁场中电子运动的回旋频率，
。
对电子运动速度进行积分，可得到电子运动轨迹方程。电子在介质平面之间运动时，两次碰撞之间的运动时间可以根据
计算得到。若发生单边放电，则根据电子在垂直于介质平面方向上位移为零得到两次碰撞之间的运动时间。
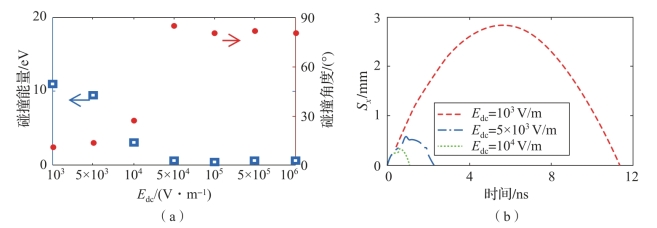
令d=5 mm和φ0=0，根据式（7-10）～式（7-17）得到在不同的射频电场强度下，从介质表面出射电子与极板碰撞时碰撞能量、碰撞角度和电子运动轨迹随表面电荷积累场强度的变化情况，如图7-8～图7-11所示，其中Sx为电子沿x方向的位移。由计算结果可知，在特定的射频电场强度下，空间中电子运动轨迹受表面积累电荷影响，影响程度与表面积累电荷场和射频电场的相对强度有关。
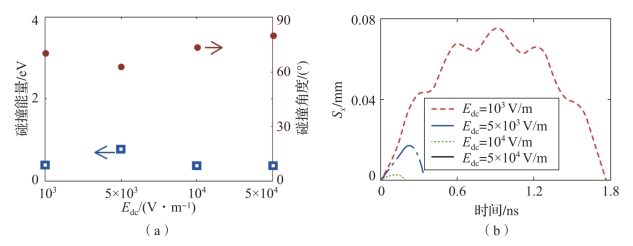
图7-8 不同电荷积累场下电子与材料表面的碰撞能量、碰撞角度和电子运动轨迹（Erf=104 V/m）（附彩图）
（a）电子碰撞能量、碰撞角度；（b）电子运动轨迹
图7-9 不同电荷积累场下电子与材料表面的碰撞能量、碰撞角度和电子运动轨迹（Erf=105 V/m）（附彩图）
（a）电子碰撞能量、碰撞角度；（b）电子运动轨迹
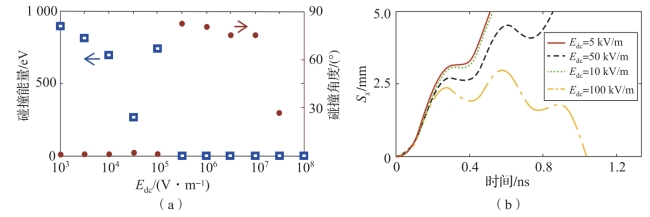
图7-10 不同电荷积累场下电子与材料表面的碰撞能量、碰撞角度和电子运动轨迹（Erf=106 V/m）（附彩图）
（a）电子碰撞能量、碰撞角度；（b）电子运动轨迹
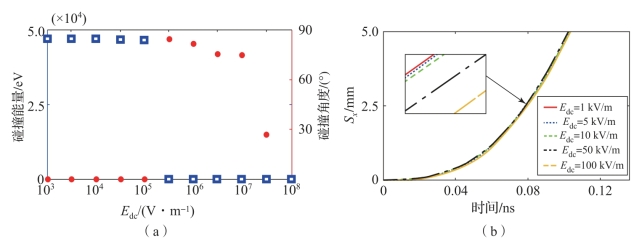
图7-11 不同电荷积累场下电子与材料表面的碰撞能量、碰撞角度和电子运动轨迹（Erf=107 V/m）（附彩图）
（a）电子碰撞能量、碰撞角度；（b）电子运动轨迹
当射频电磁场电场强度相对较弱（与表面积累电荷场可比拟）时，假设
，受表面积累正电荷场的引力影响，出射电子无法渡越磁性部件金属-介质间距，在经过多个射频周期的振荡运动后，与发射平面碰撞。此时，从下极板出射的电子受电磁场力的加速作用和积累电荷场的减速作用，同时在磁场作用下回旋运动。碰撞能量最终取决于加速周期以及电子与极板碰撞的时间，仅为数电子伏特大小，且具有一定的随机性。但是，由于电子获得的加速有限，因此与极板的碰撞能量有限。当介质表面积累正电荷场增加时，电子被迅速拉回发射极板，碰撞能量迅速降低至接近0。除此之外，电子沿x方向的最大运动距离随射频电场的强度增加而变大，碰撞能量亦随之增大。
当
时，射频电磁场电场强度足够大，使得电子能够克服表面积累正电荷场的引力影响。在经过数个射频周期的振荡运动后，电子运动到与对面极板碰撞。显然，电子碰撞能量随着表面积累正电荷场
的增大而减小。此时，电子碰撞能量可达数百eV，超过大部分金属与介质材料第一能量点E1，具备发生微放电效应的充分条件。当
增大至约0.1
时，电子无法再渡越金属-介质间距，转而与发射电子的极板碰撞。此时，碰撞能量取决于加速周期中电子与极板碰撞的时间，具有一定的随机性。随着
持续增大，电子被迅速吸收返回发射极板，碰撞能量迅速降低至接近0。
当
且
时，电子在x方向获得足够的加速，并在半个周期内迅速与对面极板碰撞。该碰撞能量随着表面积累正净电荷场
的增大而降低，但是降低幅度相对于总的碰撞能量而言非常小。此时，碰撞能量高达数万eV，远大于大部分金属与介质材料第二能量点E2，推断此时微放电效应不再发生。此时，铁氧体介质表面积累电荷场近似为
式中，N——介质表面积累的总电荷数目；
A——介质表面积，m2；
ε0——真空介电常数。
在微放电演变过程中，随着介质表面入射和发射电子数目的实时变化，Edc随时间不断变化。
综上所述，当电子不能获得足够的加速而渡越到对面的极板时，在极板间随着电磁场的变换周期进行振荡谐振运动，碰撞能量具有一定的随机性。当电子获得足够的加速并渡越到对面极板时，碰撞能量随着Edc的增加而下降。此时，电子首先加速，然后减速，最后与发射极板碰撞。然而，当Edc较大，电子无法获得足够的加速到达对面极板时，电子被迅速吸收返回发射极板，碰撞能量迅速降低至接近0。
如图7-12所示，外加磁场的量级远大于射频磁场，对电子轨迹的影响不可忽略。图中，定义Ωf=ω0·m/e，以表征电子运动回旋频率与射频磁场的比值。
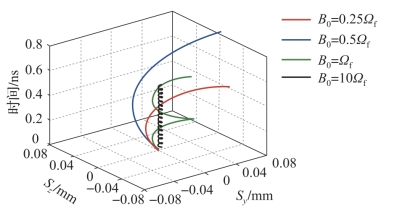
图7-12 不同静磁场作用下的电子回旋运动轨迹（附彩图）
如图7-13所示，当外加静磁场B0由0逐渐增加至0.25Ωf时，受拉莫尔回旋运动的影响，电子在电场中的运动时间变长，运动速度增大，电子与极板的碰撞能量单调递增；当B0大于0.25Ωf时，电子在极板间的运动周期小于射频电场周期，电子碰撞能量与碰撞角度在有限的范围内随机波动。
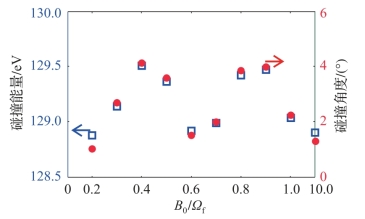
图7-13 不同静磁场作用下的电子碰撞能量和角度（附彩图）
显然，受实际外加静磁场的大小限制（远小于1 T），外加磁场对碰撞能量与碰撞角度的影响是有限的。其对电子的主要影响在于横向扩散作用。随着B0的持续增加（远大于1 T），电子的横向扩散作用逐渐截止，电子甚至在发射极板对面极板的同一位置发生碰撞。此时，由于电子从射频电磁场中获得的加速度远大于二次电子的发射速度，电子沿x方向的运动仍然占主导作用。