3.3 磁性介质表面混合电磁场分布研究
在实验测量获得平滑表面磁性介质SEY曲线并进行模型拟合后,进一步研究具有规则微结构表面磁性介质二次电子发射特性。
首先分析磁性介质表面电磁场分布特性。如图3-5所示,在具有规则微结构的真空/磁性介质界面,除了馈入的射频电磁场Erf×Brf以外,还存在外加静态磁偏置场B、由于SEE现象而产生的表面积累电荷场Edc和由于电子间互作用而产生的空间电荷场Esc。此时,表征电子运动的洛伦兹力方程可表示为
![]()
式中,v——电子的运动速度,m/s;
m——电子质量,kg;
e——电子电量,C。
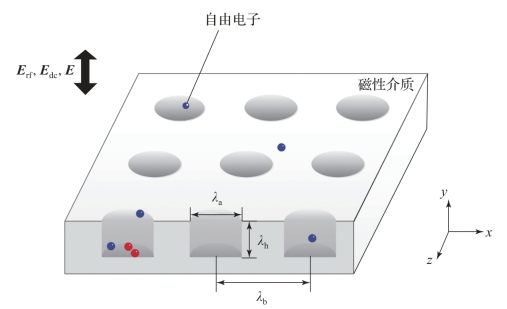
图3-5 具有人工构造微结构真空/材料界面上的电子运动原理
本节首先针对具有规则微结构金属界面电磁场分布特性和微结构中电子运动特性展开研究。对于金属/真空界面,Erf的切向分量为零,在界面上无法积累电荷。当空间中的自由电子运动进入金属表面微结构时,其运动状态受进入微结构之前电磁场作用力的影响,最终运动状态取决于微结构的物理尺寸。对于金属表面具有封闭横截面形状(如矩形、三角形和圆形)的表面微结构,射频电磁场的传输存在截止频率fc。当射频电磁场工作频率低于截止频率时,射频电磁场将不再在微结构中传输。针对不同横截面形状的电磁边界条件,求解麦克斯韦方程可以获得相应的截止频率fc。对于具有边长为wa和wb的矩形横截面,TEmn模式射频电磁场的截止频率为
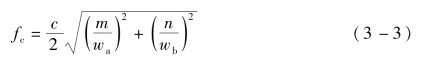
式中,c——真空中的光速,m/s;
m,n——由电磁场模式决定的正整数。
对于直径为la的圆形横截面,TEmn模式射频电磁场截止频率为
![]()
式中,u′mn——第一类m阶贝塞尔函数导数J′m(x)的第n个根。
对于直径为la的圆形横截面,TMmn模式射频电磁场截止频率为

式中,umn——第一类m阶贝塞尔函数Jm(x)的第n个根。
对于圆形横截面,等效为圆波导。其基模为TE11模,截止频率为

式中,fc11——TE11模的截止频率,GHz。
对于其他电磁场模式或者其他形状的横截面,fc可以结合具体电磁边界条件与麦克斯韦方程采用类似方法数值求解。
以圆柱形微结构为例,仅当工作频率f0>1 THz时,射频电磁场能够传输进入金属表面半径(la/2)小于数百微米的圆柱形微结构。对于工作频率远小于太赫兹频段的射频电磁场,传输进入金属表面圆柱形微结构时被截止。此时,在微结构入口端面处存在倏逝波,在微结构中电磁场逐渐衰减为零。仅当金属/真空界面上圆柱形微结构的直径la>20 mm时,工作频率为f0<10 GHz的射频电磁场能够传输进入微结构。
对于规则的圆柱形微结构阵列,定义圆柱的相对直径为
![]()
式中,la——圆柱横截面直径,m;
λ0——射频电磁场工作波长,m。
定义圆柱的相对深度为
![]()
式中,h——圆柱深度,m。
定义圆柱形微结构的表面形貌拓扑参数深宽比为
![]()
通过前述分析可知,当λa<0.58时,射频电磁场的传输将在圆柱形微结构中截止。假设f0=10 GHz,λ0=0.03 m和Sr=2,在金属材料表面建立三维圆柱形微结构阵列模型,具有不同λa的圆柱孔金属/真空界面上电场幅度分布和电性能仿真结果如图3-6和图3-7所示。
 (https://www.daowen.com)
(https://www.daowen.com)
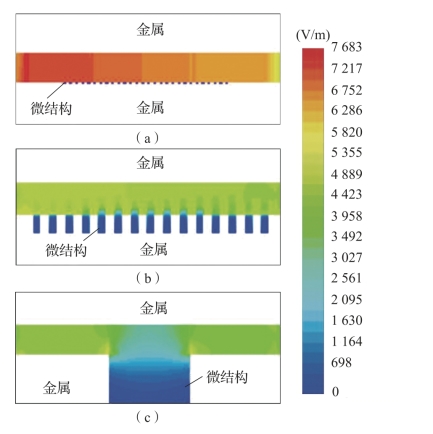
图3-6 金属/真空界面上的电场分布(附彩图)
(a)λa=0.001;(b)λa=0.01;(c)λa=0.1
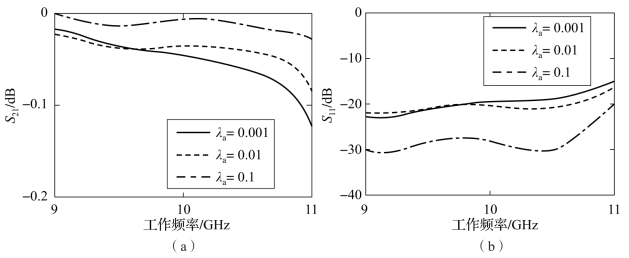
图3-7 具有不同尺寸微结构表面的阻抗变换器电性能仿真结果
(a)插入损耗S21随频率变化曲线;(b)回波损耗S11随频率变化曲线
图3-6显示了在平行金属板间,金属表面具有不同相对直径尺寸表面微结构时的电场幅度三维分布。当微结构的尺寸远小于射频电磁场工作波长(即λa<0.1)时,微结构中射频电磁场传输截止,在圆柱形微结构的端口面上存在倏逝波。当微结构的尺寸小至射频电磁场工作波长的千分之一以下时,微结构中射频电磁场分布为零,且微结构端面上的电磁场变化可以忽略。因此,当电子进入深度远大于趋肤深度的微结构时,电磁场作用力可以忽略。可以推断,电子刚进入微结构时,运动速度为非均匀;但是当电子深入微结构后,电子近似匀速运动。
如图3-7所示,当0.01<λa<0.1时,基于理想金属平面,微结构对金属微波部件电性能产生一定影响。此时改变了金属表面阻抗,对电性能的影响不一定表现为电性能的恶化,具体的变换幅度由金属微波部件物理尺寸、工作频率和微结构尺寸共同决定。当λa<0.01时,基于理想金属平面,微结构对金属微波部件电性能的影响非常微弱,可以忽略。
接下来,根据金属/真空界面上微结构中电磁场分布特性分析电子运动情况。当金属/真空界面上微结构中的电磁场传输截止时,电子在真空电磁场中获得加速或者减速,进入微结构后保持匀速运动。值得注意的是,这些孔隙在横截面上具有封闭形状。否则,电磁场将传输进入微结构,电子将以非均匀的速度运动。此时,电磁场分布和电子运动仅能通过数值方法求解。这是因为,界面上电磁场的不连续性较强,同时可能存在高阶电磁场模式。
然而,对于介质材料而言,射频电场Erf的切向分量不为零,在真空/介质界面上连续。在真空和介质中Erf垂直于界面分量的不连续性由介质材料表面积累电荷Qi决定:
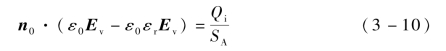
式中,n0——垂直于界面的单位法向矢量;
ε0——真空中相对介电常数;
Ev——真空中射频电场垂直于界面的分量,V/m;
εr——介质中相对介电常数;
SA——介质表面积,m2。
介质材料表面电荷积累情况与自由电子在空间中的初始分布、电子在电磁场力作用下与介质表面的碰撞和电荷输运等条件有关。为了获得介质表面微结构中电磁场分布情况解析分析,假设在电子碰撞与二次电子发射过程中介质表面积累电荷呈均匀分布。电磁场在介质表面微结构中传输,且射频电场切向分量在真空/介质界面上连续。在微结构中同时存在射频电磁场和积累电荷场。假设εr=2.1,f0=15 GHz,λ0=0.02 m,λa=0.001和Sr=1.7,在介质材料表面建立三维圆柱形微结构阵列模型,电场分布仿真结果如图3-8所示。可以看到,与金属材料不同,在介质表面三维微结构中存在电磁场分布,电子运动更为复杂。
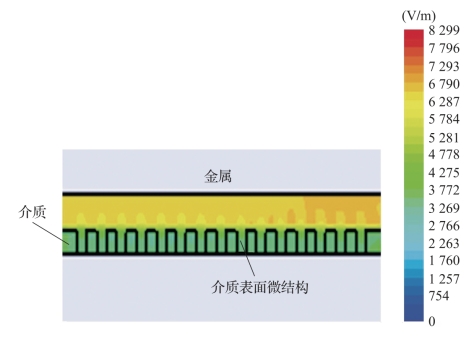
图3-8 真空/介质界面上的电场分布(附彩图)
进一步地,对于具有圆柱形微结构的磁性介质表面,由于磁性介质的外加场偏置微结构中的静态磁场B并不为零。电子主要由射频电磁场、积累电荷场和静磁场驱动。忽略在微结构侧壁上的电荷沉积和空间电荷力,介质表面微结构中电子运动受力的洛伦兹方程简化为
![]()
对于工作于GHz频段的介质微波部件,介质表面具有微米级结构尺寸的微结构中的射频电场近似为微结构端口面上射频电场幅度,即
![]()
式中,y0——微结构端口面位置,m;
Δhy——微结构中任意位置与端口面的距离,m;
h——微结构高度或深度,m。
此时,对于单载波射频电磁场而言,当Δy≪λ0且Δt≪T0时,
![]()
其中,
![]()
对于积累电荷场,可近似为

式中,Ny——入射到介质表面的电子数目;
δav——在二次电子发射过程中激发的平均SEY。
