2.2.3 基于Furman模型的SEE模拟
Vaughan模型的函数表达式简单，且在低能量段（Ein＜3Emax0）具有较好的拟合精度，因而在20世纪八九十年代的微放电数值模拟与分析中获得广泛应用。随着表面科学的发展，材料表面二次电子发射特性的测量与分析获得长足进步，实现了二次电子能量分布的测量。如前所述，通过收集不同能量段的出射电子，能够初步区分不同物理产生机制的二次电子。在此基础上，美国学者Furman等在20世纪90年代提出了可描述不同物理机制的二次电子发射模型（通常将该模型称为Furman模型），能够对真二次电子、弹性背散射二次电子和非弹性背散射二次电子分别进行曲线拟合和计算，并具有与能谱相关联的自洽特性。本书中将Furman模型应用到微放电数值模拟与分析中，使得模型表征的SEE特性更符合物理实际[6]。
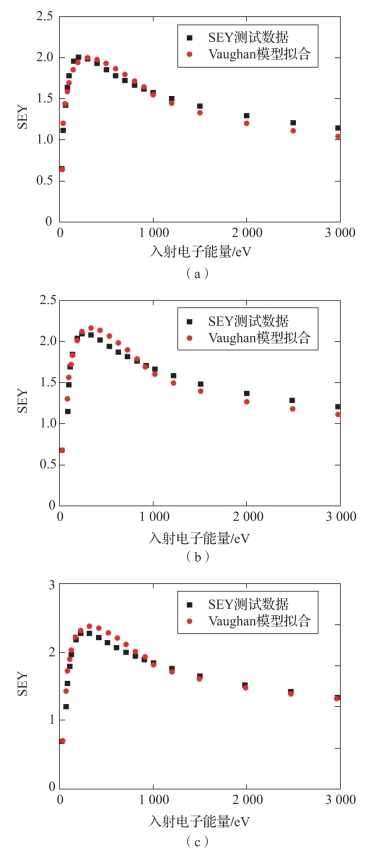
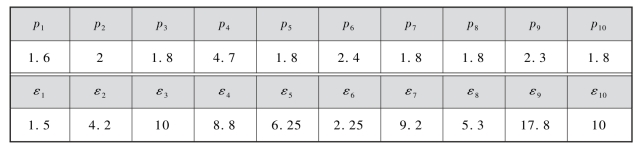
图2-7 不同入射角度下未采用离子清洗的铝合金镀银样片SEY曲线测量值与模型拟合值（附彩图）
（a）0°；（b）20°；（c）40°
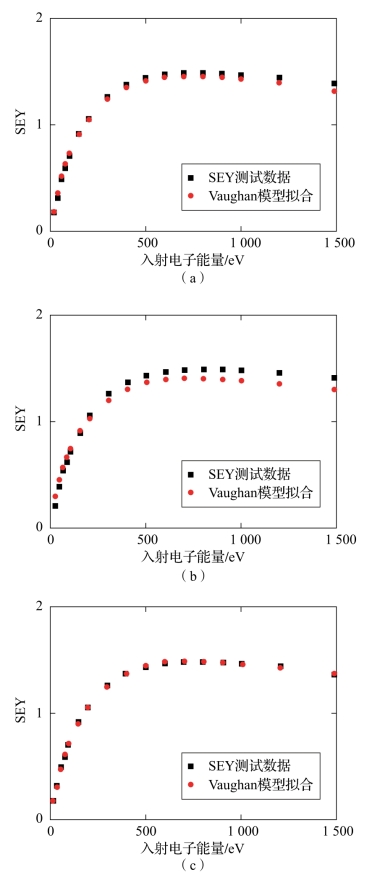
图2-8 不同入射角度下采用离子清洗的铝合金样片SEY曲线测量值与模型拟合值（附彩图）
（a）0°；（b）20°（c）40°
如前所述，二次电子发射物理过程可以简要描述为以下过程：当电子束eN入射到材料表面上时，一些电子会发生弹性漫反射（这一部分SEY定义为δe），另一部分电子进入材料。进入材料的电子将分为两部分：不与材料原子发生作用并直接散射的电子定义为非弹性背散射SEY δr；与材料原子直接作用，并从中激发出的二次电子定义为真SEY δt。相应地，取决于入射能量Ein与入射角度θin，总SEY δtotal的计算见式（1-1）。
SEY与能谱满足自洽关系的SEE模型必须满足如式（1-2）所示的微分表达式。此时，一定入射电子能量和角度下出射电子能量分布为SEY随能量的微分。同时，应当满足SEY为能谱的积分：
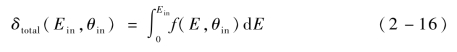
首先讨论一定入射电子能量和角度下出射真SEY δt：
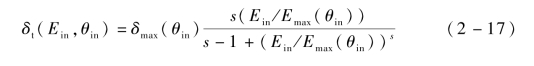
式中，
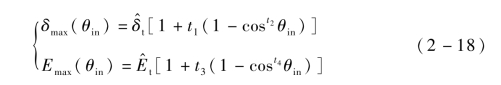
式中，s——真SEY曲线的拟合参数；
t1，t2，t3，t4——不同入射角度下真SEY曲线的拟合参数；
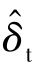——真SEY δt的峰值；
——
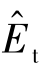对应的入射电子能量，eV。
与Vaughan模型采用平方函数作为基函数不同，Furman模型采用余弦函数的指数形式表示真SEY随不同入射角度的变化。同时，角度拟合参数由1个增加为4个，能够针对入射电子能量和出射产额分别进行拟合，拟合准确度更高，但拟合过程也更复杂。
当出射二次电子的总产额δtotal≤1时，出射二次电子为弹性背散射电子的概率为
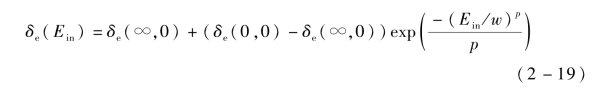
式中，w，p——垂直入射情况下，弹性背散射电子出射概率曲线的拟合参数。
考虑不同入射角度下的散射效应，将式（2-19）修正为
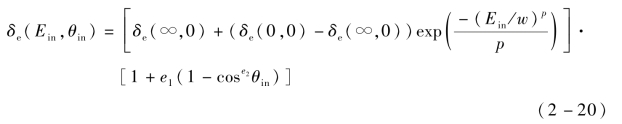
式中，e1，e2——不同入射角度下，弹性背散射电子出射概率曲线的拟合参数。
当出射二次电子的总产额δtotal≤1时，出射二次电子为非弹性背散射电子的概率为
式中，r——垂直入射情况下，非弹性背散射电子出射概率曲线的拟合参数。
考虑不同入射角度下的散射效应，将式（2-21）修正为
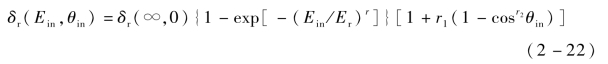
式中，r1，r2——不同入射角度下，非弹性背散射电子出射概率曲线的拟合参数。
在Furman模型中，针对真二次电子、弹性背散射二次电子和非弹性背散射二次电子采用同样的随角度散射效应修正因子。这是因为，对于现有的二次电子发射测试平台，受限于电子运动的随机性与环境因素的影响无法完全理想屏蔽，导致无法以更高的分辨率测量不同入射角度下的二次电子发射曲线与能谱。因此，无论Vaughan模型还是Furman模型，均无法对不同入射角度下的二次电子发射特性实现更为准确的模拟和拟合。
Furman模型采用近似满足式（1-2）的函数实现不同类型二次电子的能谱分布表达，则不同二次电子的SEE能谱分别为
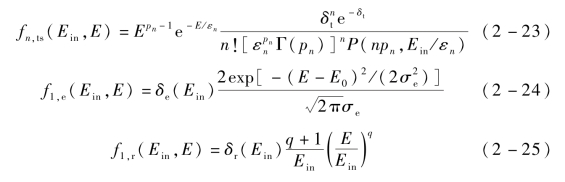
其中，
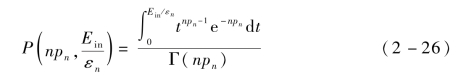
式中，Γ（x）——格林函数；
σe，q——曲线拟合参数；
pn，εn——曲线拟合参数，pn＞0。
理论上，采用式（1-2），对式（2-18）～式（2-26）作微分计算，将得到真二次电子、弹性背散射电子和非弹性背散射电子的出射能量E的概率密度分布函数。
对于微放电效应中的二次电子发射特性模拟，采用Furman模型对随机入射的电子云与材料碰撞时每次碰撞产生的二次电子数量、能量和角度分布进行描述。此时，非弹性背散射和弹性背散射电子只在仅有一个电子出射时存在。当δtotal=1时，采用一个数值在0～1均匀分布的随机数判断出射电子属于真二次电子、非弹性背散射电子还是弹性背散射电子。当δtotal＞1时，采用真二次电子发射能谱描述δtotal的能量分布。
图2-5所示为不同入射角度下铝合金镀银样片的SEY曲线。最大SEY δmax（θin）与其对应的入射电子能量Emax（θin）能够从SEY测试数据中直接获取。
典型SEE能谱曲线如图1-7所示，根据出射能量可将其分为三个区域——真二次电子区域、非弹性背散射区域与弹性背散射区域。分别对真二次电子能量区域和弹性背散射峰进行积分得到
和
，则
。
在曲线拟合过程中，定义δe（0，0）为可调参数，在较小的范围内进行微调，既不影响物理特性，又能较好地实现实验数据的拟合。其他曲线形状拟合参数可以调整到逼近测量数据。
根据式（2-16）～式（2-26），结合实验结果得到Furman模型拟合参数，建立铝合金镀银样片的SEE特性数值概率模型。与SEE测试结果对比，模型数据与其吻合良好，如图2-9、图2-10所示。
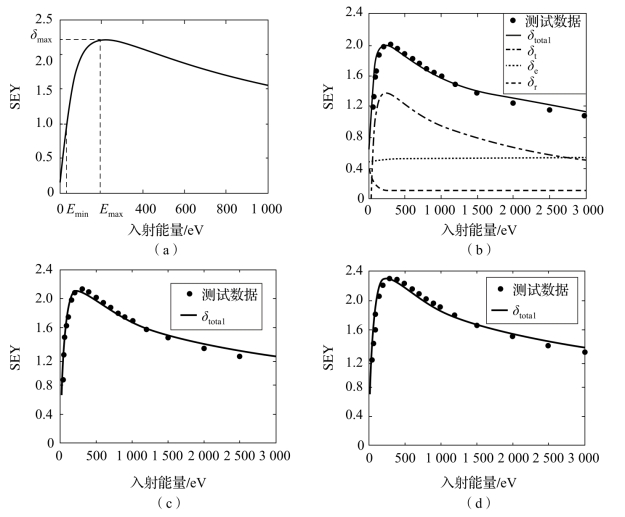
图2-9 铝合金镀银样片的SEY测试结果与模型拟合结果对比
（a）垂直入射时SEY测量结果；（b）采用Furman模型拟合得到的SEY曲线；（c）采用Furman模型拟合得到20°入射角度时的总SEY曲线；（d）采用Furman模型拟合得到40°入射角度时的总SEY曲线
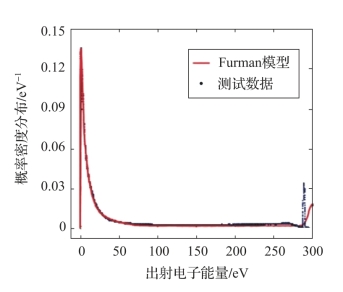
图2-10 铝合金镀银样片的SEE能谱曲线（附彩图）
结合前述的测量与数值拟合结果，对Vaughan模型和Furman模型的拟合精度进行比较分析。对铝合金镀银样片在不同入射角度下的SEY曲线测量值进行拟合，当采用Vaughan模型时，入射角度为0°时的相对误差为-8%～8%，入射角度为20°时的相对误差为-8%～13%，入射角度为40°时的相对误差为-2%～19%；当采用Furman模型时，入射角度为0°时的相对误差为-8%～8%，入射角度为20°时的相对误差为-3.0%～0.5%，入射角度为40°时的相对误差为-6.0%～0.4%。针对铝合金镀银材料，当垂直入射时，采用Vaughan模型和Furman模型拟合的精度范围一致。Vaughan模型具有拟合参数较少、拟合过程简单的优势，但无法区分不同的二次电子散射机制，亦不能对能谱进行拟合。Furman模型能将出射电子区分为真二次电子、弹性背散射电子和非弹性背散射电子，更符合物理实际，同时，由于区分了三种二次电子，因此能够针对出射能谱进行拟合，但Furman模型存在拟合参数过多，拟合过程复杂的缺陷。在实际数值模拟中，应根据实际应用场景进行具体选择。本书中仅针对铝合金镀银材料的拟合精度进行了对比，更多材料的拟合精度需要在未来工作中进一步研究与讨论。
采用Furman模型对铝合金镀银样片进行拟合的参数如表2-2和表2-3中所示。
表2-2 采用Furman模型对铝合金镀银样片的SEY特性拟合参数
续表
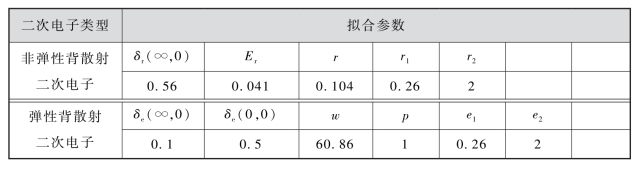
表2-3 铝合金镀银材料Furman模型能谱拟合参数
