3.4.1 介质表面微结构中电子轨迹追踪算法
当电子以一定速度vini和角度θini入射到介质表面微结构后，受混合电磁场力作用，做变速回旋运动。将电子运动分解为三维回旋运动和沿电场线方向的匀变速直线运动。如图3-5所示，假设在单个微结构中外加静磁场分布均匀，则电子回旋半径为
回旋角频率为
令微结构端口面圆心位置为原点，结合回旋运动方程与微结构边界条件，可得到电子与微结构碰撞时间tc与碰撞位置sc。
电子匀变速直线运动方程为
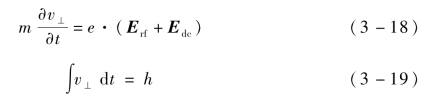
式中，v⊥——电子沿垂直于端口面方向速度，即图3-5中速度的y方向分量，m/s。
结合匀变速运动方程与微结构边界条件得到电子与微结构碰撞时间与碰撞位置。根据电子运动发生碰撞的最短时间判断得到电子与微结构碰撞时间ti。此时若满足不碰撞出射条件，即
则入射电子不与微结构碰撞而直接出射，总SEY δtotal计数加1。
如果入射电子与微结构碰撞，则根据电子回旋运动得到碰撞时电子速度vin、碰撞位置sin和碰撞角度θin。根据SEE模型，得到出射SEY、能量分布与角度分布。以出射电子位置so（xo，yo，zo）、速度vo和角度θo作为初始条件，计算求解出射电子在微结构中的回旋运动与匀变速运动方程，根据电子运动发生碰撞的最短时间进行判断，得到电子与微结构再次碰撞时的时间to。判断二次电子是否满足出射条件：
式中，vo⊥——电子出射速度沿垂直于端口面方向分量，m/s。
若二次出射的电子不再与微结构碰撞而直接出射，则总SEY δtotal计数加1；否则，记录再次碰撞时间、位置、能量和角度，根据SEE模型计算下一次出射的电子。通常，入射电子经过一次碰撞后出射的二次电子能量较低（＜50 eV），同时在λa＜0.1的微结构中获得的加速度较小，再次碰撞时很难有二次电子出射。因此，对于一个初始入射电子而言，经过三次以上的SEE过程，则其激励的所有二次电子将从微结构中出射或者被介质材料吸收，不再出射。采用蒙特卡洛数值模拟，构造服从一定随机性分布的初始电子，按照以上算法过程进行迭代计算，可得到具有微结构介质材料表面等效SEY。