7.4.1 微放电电磁场演变与电子运动数值计算
在7.3节的等效模型中,分析了混合电磁场分布下服从洛伦兹力的电子运动过程。如图7-14所示,铁氧体环行器微放电效应不仅涉及电磁场作用下的电子运动,还涉及二次电子发射以及二次电子与电磁场作用的耦合迭代过程。铁氧体环行器微放电三维数值模拟与阈值功率分析对每个物理过程的建模与分析均提出了较高的计算精度要求。对于实际磁性微波部件,解析解的精度不再满足需要,需要求助于数值方法。作为微放电效应数值模拟的基础,首先需要建立铁氧体环行器的三维模型并进行合适的网格剖分,以便进行后续的电磁场计算与电子运动推进计算。
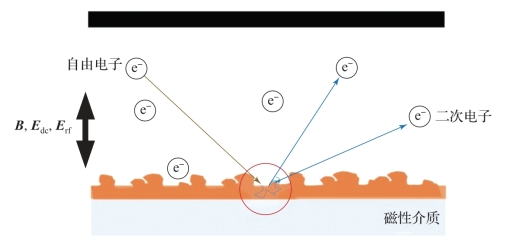
图7-14 磁性微波部件微放电电子与边界作用物理过程示意图
在离散后的网格中根据FDTD算法,求解麦克斯韦方程组,得到电磁场随时间与空间的分布:
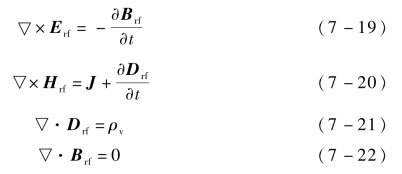
式中,Erf——射频电场矢量,V/m;
Drf——电通量密度矢量,C/m2;
Hrf——射频磁场矢量,A/m;
Brf——磁通量密度矢量,Wb/m2;
J——空间中的电流源,A/m2;
ρv——空间中的电荷源,C/m3。
介质材料特性与电磁场分布关系可由本构方程进行表征:

式中,ε——电磁场所在空间的介质介电常数,F/m;
μ——电磁场所在空间的介质磁导率,H/m。
对于各向同性介质而言,ε和μ为常数,且沿各个方向上的分量相等。对于各向异性介质(如铁磁性介质),ε(或μ)可表示为张量形式ε(或μ),通过式(7-1)~式(7-5)进行计算。(https://www.daowen.com)
针对磁性介质微波部件,建立边界条件,在FDTD算法中采用差分形式实现时间域和空间域的微分计算[6-8]:
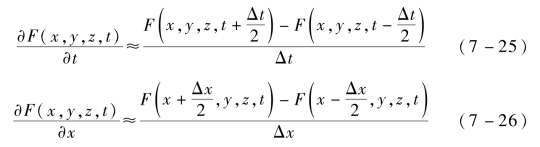
式中,F(x,y,z,t)——差分算子,表示式(7-19)~式(7-22)中各矢量分量时间为t时在位置(x,y,z)处的值;
Δt——数值模拟时间步长,s;
Δx——单位网格在x方向上的长度,m。
然后,在Yee网格中采用FDTD算法计算得到任意时间步长时任意网格节点上的电磁场分量,随时间推进迭代运算,获得空间中电磁场分布。当网格剖分合理时,计算精度与数值效率可以得到保证。
接下来,根据铁氧体环行器的实际应用情况预定义载波信号,同时在输入端口的网格中进行激励。对于微放电数值模拟而言,与电性能计算不同,载波信号不再采用高斯信号,而是采用周期性单音或多音信号,形如
![]()
式中,N——输入载波数;
ωi——第i路载波的角频率;
φi——第i路载波的相位。
采用宏粒子(或粒子)模拟微放电中的初始电子与二次电子,假设每个粒子为M个电子的质量与电荷量。
对应于铁氧体环行器中的初始自由电子分布,在铁氧体环行器腔体中真空部分的网格中采用初始粒子进行模拟。初始粒子可根据实际仿真需要设置为随机分布、固定发射等。初始粒子能量的取值范围一般为0到数个eV之间随机分布,初始相位的取值范围在0°~180°之间随机分布(0°表示垂直于环行器表面)。由于初始电子在与器件表面碰撞时将消失,因此决定微放电击穿阈值的主要因素为碰撞发射的SEY与能量、角度分布。由于初始电子与边界碰撞时的能量和角度决定了出射的二次电子特性,因此需要对初始电子能量和角度分布进行预分析,以实现微放电数值模拟结果收敛。网格节点上的电磁场幅度初始值始终设置为零。
对于自由空间中的电子而言,电子动力学(包括运动速度v与运动位移r)服从洛伦兹力方程。由于电子运动速度远低于光速,因此不考虑相对论性。为了与电磁场方程随时间步推进的数学形式保持一致,得到第n个时间步时洛伦兹力方程的差分形式为
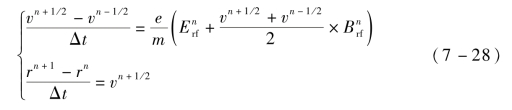
任意空间位置粒子处的电磁场值可通过对空间位置所在网格节点上的电磁场值进行插值得到。同时,电子运动对网格中的电磁场演变产生影响,同样采用插值算法将电子运动产生的电荷和电流变化计入电磁场演变,实现电子与电磁场耦合迭代演变数值模拟。
