3.4.3 具有微结构磁性介质SEY的蒙特卡洛模拟结果
采用蒙特卡洛模拟方法,对具有规则微结构阵列的磁性介质表面二次电子发射特性进行计算和模拟。假设磁性介质表面微结构的孔隙率为ρ,ρ表示微结构所占表面积与磁性介质总表面积的比值。ρ越大,则表面微结构的所占比例越大。采用图3-9所示的算法,并结合蒙特卡洛模拟对单个微结构中的电子入射、碰撞、二次电子发射和电子出射进行追踪,得到三维空间中单个微结构中电子出射个数与入射个数的比率,即单个微结构SEY值δt。假设平滑磁性介质表面SEY为δf,则具有微结构表面SEY为
![]()
图3-11所示为圆柱形微结构磁性介质/真空界面上不同深宽比Sr下的SEY曲线。设置入射初始电子数目为5 000,λa=0.001,Edc=10 V/m和B=0.001 T。
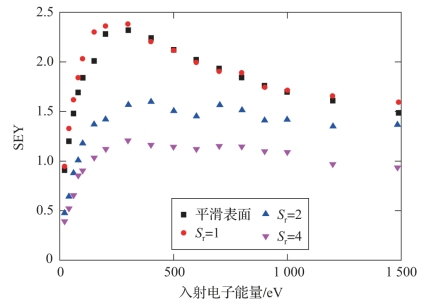
图3-11 具有微结构磁性介质/真空界面上不同Sr下的SEY曲线(附彩图)
当电子运动进入磁性介质表面的圆柱形微结构时,电子以回旋运动的形式获得加速。电子或空穴的沉积会形成表面势垒。若电子运动并与微结构边界碰撞,则发射具有更低能量的二次电子,那些无法克服表面势垒的二次电子将被介质吸收。此时,在磁性介质/真空表面形成了电子束缚效应,实际的SEY降低。当Sr≥2时,微结构对电子的束缚效应开始显现,从界面上出射的最大SEY降低至小于1.5。随着微结构深度的增加且Sr≥4,电子束缚效应越发显著,平均SEY接近于1,此时不易发生微放电。而当Sr≤1,即微结构的宽度大于或等于深度时,表面微结构对SEE产生增强效应。根据模拟结果可知,表面微结构对材料SEE特性具有增强(或抑制)作用,起增强作用还是抑制作用及其作用效果与微结构的深宽比Sr有关。
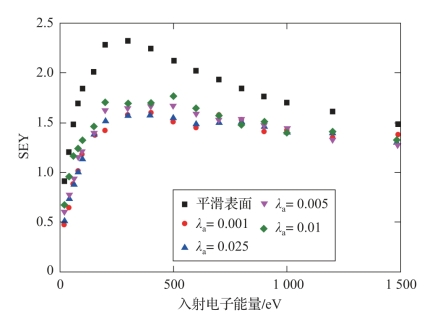
图3-12所示为具有同样深宽比和不同绝对物理尺寸微结构的磁性介质表面SEY。此时,Sr=2,B=0.001 T,Edc=250 V/m,λh=3.1×10-3和f0=3 GHz。可以看到,相较于深宽比,绝对物理尺寸对SEY的影响较微弱。对于具有不同物理尺寸和相同深宽比微结构磁性介质表面,可以通过蒙特卡洛模拟得到几乎相同的SEY曲线。相对而言,绝对尺寸越小,微结构对二次电子的束缚作用就越明显。根据模拟结果推断,影响表面SEY的主要因素为微结构的深宽比Sr。
 (https://www.daowen.com)
(https://www.daowen.com)
图3-12 具有微结构磁性介质/真空界面上不同λa下的SEY(附彩图)
如图3-13所示,为不同Edc条件下具有微结构磁性介质/真空界面上模拟得到的SEY曲线。此时,Sr=2,B=0.001 T,λa=1.6×10-3,λh=3.1×10-3和f0=3 GHz。
当磁性介质表面积累负电荷时,对入射电子和出射二次电子产生排斥力;当磁性介质表面积累正电荷时,对入射电子和出射二次电子产生吸引力。相较于平滑表面,深宽比Sr=2的微结构对磁性介质SEY产生明显的抑制作用。当磁性介质表面带负电时,微结构对SEY的抑制作用仍然存在。但是,随着表面积累负电荷进一步增加,受电荷斥力影响,电子可能无法入射到微结构中,即无法产生发射。由模拟结果可知,介质表面积累的正电荷对于SEY有额外的抑制作用。Edc越大,SEY抑制效果越明显。随着介质表面积累正电荷导致的场强度从0到103 V/m逐渐增大,从磁性介质表面微结构中出射的二次电子逐渐减少,抑制作用增强。这是因为,电子与微结构边界碰撞时,产生的二次电子往往具有较低的能量,若此时受到正电荷吸引力回到介质表面,则对SEY有进一步的抑制作用。可以推测,当介质微波部件发生微放电时,大量出射二次电子,介质表面积累正电荷,将削弱微放电的产生。因此,在需要进行SEY抑制的应用场合,可通过外加静态正电荷偏置实现SEY的整体降低与抑制。
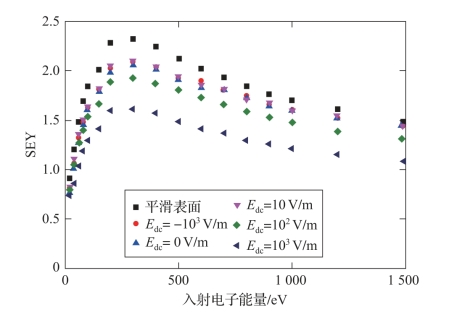
图3-13 具有微结构真空/磁性介质界面上不同Edc下的SEY(附彩图)
图3-14所示为不同外加静态磁场偏置条件下具有微结构磁性介质/真空界面上模拟得到的SEY曲线。此时,Sr=2,Edc=250 V/m,λa=1.6×10-3,λh=3.1×10-3和f0=3 GHz。电子在微结构中运动时,受到射频电场力、表面积累电荷场和外加静态磁场的共同作用,做变速回旋运动。根据式(3-16),电子回旋半径不仅与外加磁场有关,还与电子入射到微结构中的运动速度有关。模拟结果表明,当B≥10 T时,电子回旋半径远小于微结构半径,此时电子垂直回旋入射到微结构的底部,然后垂直回旋出射,微结构对界面SEY不再产生影响,与平滑表面的SEY几乎相同。当B=1 T时,若电子的入射速度较小,则回旋半径较小,大部分随机入射的电子不与微结构边界发生碰撞,与B≥10 T时的情况一致,微结构对界面SEY不再产生影响,与平滑表面的SEY几乎相同;然而,随着入射电子能量增加,电子回旋半径增大,入射电子与微结构边界发生碰撞,当电子回旋半径增大至几乎所有的入射电子均与微结构边界发生碰撞时,微结构对入射电子的束缚作用开始显现。随着外加磁场减小至B=0.1 T,电子回旋半径远大于微结构半径,则微结构对入射电子的束缚作用最强。随着外加磁场的进一步减小,微结构对入射电子的束缚作用保持不变。
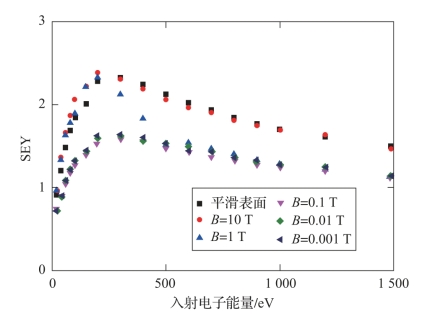
图3-14 具有微结构真空/磁性介质界面上不同B下SEY曲线(附彩图)
