3.4.2 二次电子发射模拟中的坐标变换
如图3-10所示,在二次电子发射数值模拟算法中,为了计算任意位置处的电子碰撞入射与二次电子出射情况,往往需要进行坐标变换。对于在空间中运动的电子,其全局坐标用于电磁场分布的计算与电子运动的推进,采用笛卡儿坐标系定义为(x,y,z);其局部坐标用于具体碰撞位置处的电子碰撞计算,采用笛卡儿坐标系定义为(x′,y′,z′)。在进行磁性介质微结构中SEE模拟时,需要将电子在空间中运动时所处的全局坐标变换为碰撞位置处的局部坐标,或者将出射的二次电子的局部坐标变换为全局坐标。
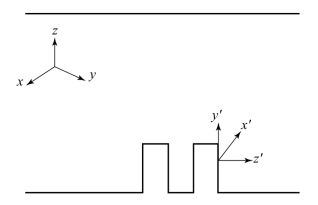
图3-10 坐标变换示意图
1.入射电子碰撞角度的计算
根据3.4.1节算法对入射电子轨迹进行计算和追踪。当电子在全局坐标中以速度vi(vxi,vyi,vzi)与微结构介质边界在si(xi,yi,zi)处发生碰撞时,需要得到电子与介质碰撞的能量Ei和角度θi并将其作为SEE模型的输入,以计算碰撞时的二次电子发射。碰撞能量可根据碰撞速度直接计算获得。对于碰撞角度,首先应根据微结构曲面形状计算碰撞位置处的法向量。若介质表面微结构曲面形状可在直角坐标系中用函数F(x,y,z)表示,则si(xi,yi,zi)处的法向单位矢量为
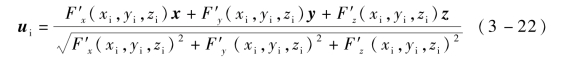
式中,F′x(xi,yi,zi)——F(x,y,z)对x的偏导数在si(xi,yi,zi)处的值;
F′y(xi,yi,zi)——F(x,y,z)对y的偏导数在si(xi,yi,zi)处的值;
F′z(xi,yi,zi)——F(x,y,z)对z的偏导数在si(xi,yi,zi)处的值;
x,y,z——直角坐标系中沿x轴、y轴和z轴的单位矢量。由此,入射电子碰撞角度为
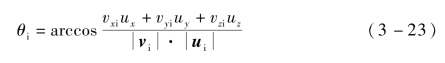 (https://www.daowen.com)
(https://www.daowen.com)
根据式(3-22)和式(3-23),可获得入射电子与介质表面碰撞角度。若是形状规则的微结构,则往往可以根据结构形状直接定义碰撞位置处表面法向量。结合入射电子能量Ein,将θin代入SEE模型,即可计算二次电子发射。
2.出射电子坐标变换
由于在SEE模型中采用随机余弦分布模拟二次电子出射角度,因此在局部坐标中采用圆柱坐标系。若碰撞位置处曲面的单位法向矢量为uin(ux,uy,uz),定义电子出射方向与uz的夹角为θ′、与ux的夹角为φ′,则出射电子在局部直角坐标系中的坐标(xx′,yy′,zz′)为

因此,(xx′x′,yy′y′,zz′z′)为以夹角(θ′,φ′)出射电子在局部直角坐标系中的出射方向。
将全局坐标系中任意坐标(xin,yin,zin)变换到局部坐标系中时,局部坐标为(xxin,yyin,zzin),则
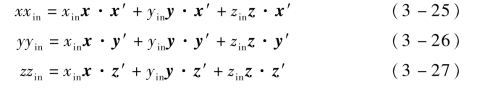
则坐标变换矩阵为
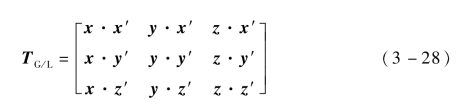
当按照式(3-24)得到出射二次电子的局部坐标后,根据局部坐标系到全局坐标系的坐标变换矩阵T′G/L得到全局坐标系中的坐标(x,y,z):

