7.4.3 铁氧体环行器微放电三维数值模拟
7.3节通过对铁氧体介质表面电子运动轨迹的解析求解，研究了外加静磁场偏置和表面积累电荷对微放电电子运动轨迹的影响，但是计算精度对于实际铁磁性微波部件的定量微放电分析和阈值研究而言远远不够。因此，本节采用数值计算获得实际铁磁性微波部件内部的电磁场分布，收敛精度达到小于-40 dB。研究中结合粒子模拟方法和材料SEE数值模型，实施铁氧体环行器微放电效应三维数值模拟，在数值模拟中考虑了铁氧体介质表面的电荷积累和外加磁场偏置的影响。图7-17所示为铁氧体环行器微放电三维数值模拟流程示意图。
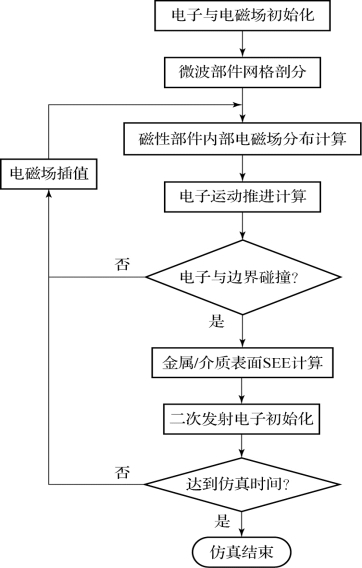
图7-17 铁氧体环行器微放电三维数值模拟流程示意图
相较于金属微波部件，磁性介质微波部件中的电磁场分布具有更强的非均匀性和空间复杂度，因此需要更高的电磁计算收敛精度。一旦获得每个时间步任意网格上的电磁场分量，便能通过插值算法获得任意位置处的电磁场值并对粒子运动进行驱动。外加静磁场偏置的计算，以及磁性介质微波部件磁介质各向异性的分析，均耦合在电磁场数值计算中。对于第n个时间步时，收集在介质表面发生碰撞的入射粒子数及出射粒子数，计算该时间步时介质表面积累的电荷数，并利用泊松方程计算。理论上，根据本章中电磁场演变与电子运动的差分表达式（式（7-28）），随时间步进行推进，即可得到粒子的运动速度和位移，进而可以对粒子进行驱动。铁氧体环行器微放电数值模拟的主要流程如下：
第1步，加载初始粒子，即粒子源。
第2步，利用FDTD算法更新求解区域内的电磁场分布，获得所有Yee网格上的电磁场值。
第3步，根据第2步获得的电磁场值，插值得到每个粒子所在位置处的电磁场值。
第4步，根据式（7-28），对粒子进行驱动。
第5步，判断粒子是否通过金属/介质边界，若通过，则利用二次电子发射模型激发新的二次粒子。
第6步，粒子运动将产生电流，利用插值原理将电流分配到各个棱边。
第7步，将产生的电流作为源引入麦克斯韦方程。
第8步，重复第2～7步，直至达到仿真终止条件。