4.3.1　在线标定误差模型

4.3.1　在线标定误差模型

为简化标定模型，不考虑惯性器件安装误差，则不考虑安装误差的陀螺仪误差模型为

式中，δkgx、δkgy、δkgz分别为陀螺x、y、z轴 刻度 系数 误差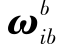；为陀螺输出的角速度；εb为陀螺随机常值漂移。

不考虑安装误差的加速度计误差模型为

式中，fb为加速度计输出的比力；δkax、δkay、δkaz分别为加速度计x、y、z轴的刻度系数误差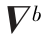；为加速度计随机常值零偏。

将式（4-29）、式（4-30）代入惯导速度误差方程和姿态误差方程，组成在线标定的基本方程。为便于进行可观测性分析，考虑到地球自转角速度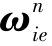和导航坐标系相对于地球坐标系的角速度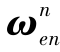的量级相对加计零偏和陀螺漂移及姿态误差的量级要小很多，加上标定的时间很短，在误差模型中略去与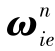和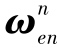相关的项，于是采用类似传递对准的思想，借助主惯导的速度和姿态信息作为匹配量，构建如下的状态空间模型：

其中，X＝［δVnφnμbδka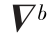δkgεb］T，W、V为互不相关的高斯白噪声。

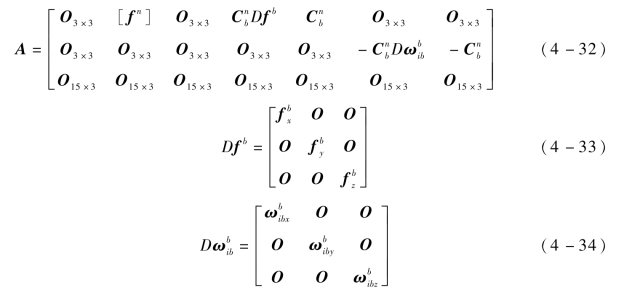
式中，［fn］为fn的反对称矩阵；μb为子惯导相对主惯导的安装误差角。

量测矩阵：