7.2.2 两阶段卡尔曼滤波算法
2026年01月15日
7.2.2 两阶段卡尔曼滤波算法
两阶段卡尔曼滤波,顾名思义就是将滤波分成两步进行。在一定的代数限制下,两阶段卡尔曼滤波与扩展卡尔曼滤波具有等价性。两阶段卡尔曼滤波算法针对的是如下系统模型:
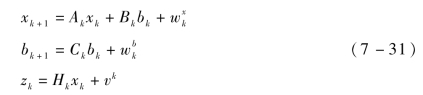
其中,xk为n维状态变量;bk为q维偏差量;zk为m维量测量;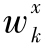 、
、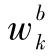 、vk分别为相应维数的高斯白噪声序列,其统计特性如下:
、vk分别为相应维数的高斯白噪声序列,其统计特性如下:
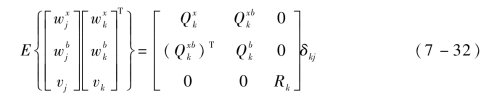
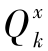 、
、 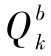 、Rk都大于0。δkj为Kronecker delta函数。其具体步骤如下。
、Rk都大于0。δkj为Kronecker delta函数。其具体步骤如下。
第一步,忽略偏差量(即令bk=0)得到无偏滤波器,其和标准的卡尔曼滤波器有相似的结构。即
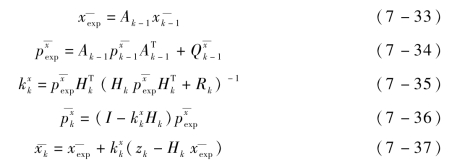
第二步,估计偏差量,其滤波算法如下:(https://www.daowen.com)
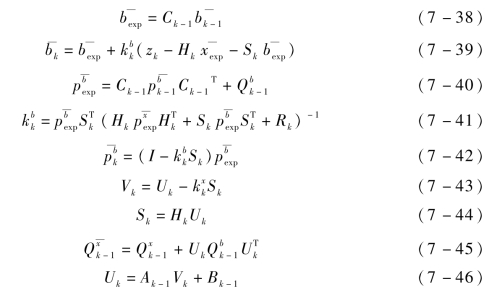
然后将无偏滤波器结果和状态变量结果融合得到状态变量估计值为
![]()
两阶段卡尔曼滤波将扩展卡尔曼滤波分解成两个降阶滤波器,并且两个降阶滤波器可以并行运算,大大减少了滤波计算量。设无偏差滤波器的状态维数为n,偏差滤波器的维数为p,则扩展卡尔曼滤波的维数为(n+p)。根据文献[72]的公式,迭代一次时,扩展卡尔曼滤波的计算量为
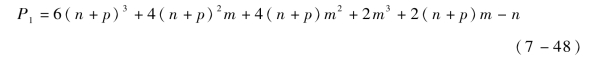
而两阶段卡尔曼滤波的计算量为
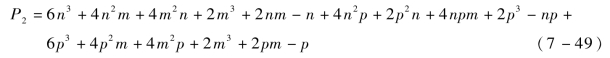
当p越大时,两阶段卡尔曼滤波的优势越明显。
