7.2.1　基于模型预测滤波的降维理论

7.2.1　基于模型预测滤波的降维理论

模型预测滤波是针对非线性系统模型的滤波方法，其核心思想是用预测输出跟踪测量输出，从而估计出系统的模型误差。

考虑如下的非线性系统：

式中，f∈Rn为非线性函数；D为模型误差；G为模型误差矩阵；x为状态变量；Z∈Rm为量测变量；h为量测矩阵；v为零均值高斯白噪声，协方差E｛vvT｝＝R。

状态估计和预测输出估计的关系如下：

记h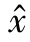（）的第i个分量为hi，i＝1，…，m。对式（7-18）的第二个等式连续微分，并将式（7-19）的第一个表达式代入等式右端，记D的任何分量第一次出现在hi的微分中的最低阶数为pi。取小的时间间隔Δt，并展开成pi阶泰勒级数，同时忽略高阶项，得到

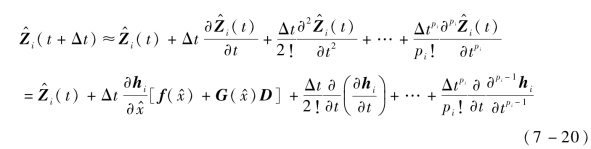
根据李导数定义k阶李导数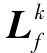（hi）。

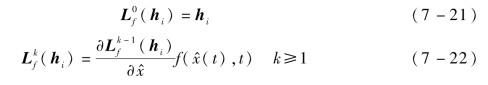
由于D的任何分量第一次出现在hi的微分中的最低阶数为pi，当阶数小于pi时，，于是式（7-20）可写为

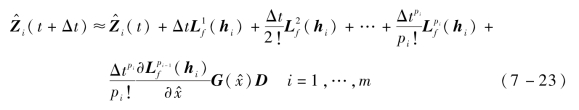
将式（7-23）写成矩阵形式，可得

其中，Λ（Δt）∈Rm×m为对角阵，其对角元素为

标量函数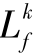（hi）关于向量场gj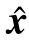（（t），t）的一阶李导数记为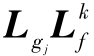（hi）：

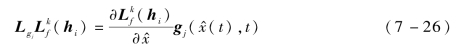
U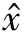（）是灵敏度矩阵：

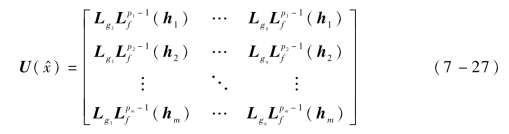
gj为G的第j列，j＝1，…，m。

S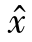（，Δt）为n1维列向量，其各分量为

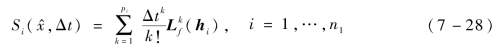
定义如下性能指标函数：

式中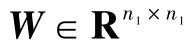，为模型误差加权矩阵。

假定小的时间间隔为常数，Z（t）＝Zk，Z（t＋Δt）＝Zk＋1。为了使J最小，需满足，由此可得［tk，tk＋1］时间区间的模型误差估计：

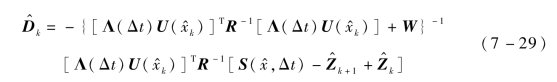
令Mk＝｛［Λ（Δt）U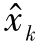（）］TR-1［Λ（Δt）U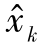（）］＋W｝［Λ（Δt）U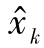（）］TR-1，则式（7-21）可写成

运用预测滤波进行在线标定时，往往将待标定的误差项看作模型误差，系统状态变量的维数大大降低，从而减少了滤波计算量，提高了标定的实时性。