7.2.3　基于序贯处理的平方根滤波

7.2.3　基于序贯处理的平方根滤波

针对无偏滤波器存在因计算误差易使误差协方差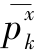逐渐失去非负定性，从而导致滤波发散的不足。信冠杰等［75］针对该缺陷将Q-R分解引入卡尔曼滤波，提高了滤波稳定性。本书引入基于序贯处理的平方根滤波算法。

平方根滤波的核心思想是将误差协方差进行平方根分解即Pk＝Δk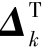，Pexp＝Δexp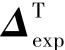。在滤波计算过程中只对Δexp和Δk进行计算，由于Δexp和Δk的特殊形式，从而保证Pexp和Pk的非负定性。

设系统方程和量测方程为

式中，Wk和Vk都为零均值白噪声；方差阵分别为Qk和Rk；Wk和Vk相互独立。

记：

量测为m维向量。对于m维独立量测的情况，量测噪声方差阵为对角阵：

则平方根滤波的量测更新可采用序贯处理来实现。

设根据k-1时刻的序贯处理结果已获得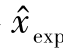和Δexp，则k时刻的量测更新序贯处理按下述步骤进行。

取：

对于j＝1，2，…，m，迭代计算方程（7-54）～方程（7-59）：

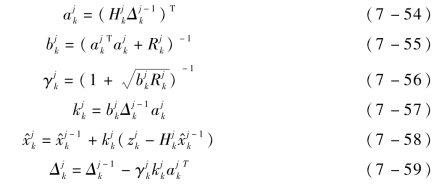
当j＝m时，即获得k时刻的量测更新结果：