4.4.2 仿真分析
假设炮车做如下运动。
静止一段时间,然后加速运动,给予炮车一定的速度,接着以变角速度通过一座拱桥,待姿态调平后,摇架在水平方向转动360°,然后炮车做变加速运动的同时摇架按正弦规律做俯仰和偏航角运动,一段时间后,炮车以变加速度做圆周运动的同时摇架按正弦规律做俯仰和偏航角运动。
通过拱桥可以使天向加速度计有比力变化,水平变加速及摇架摇摆运动可以满足可观测性原则(1),变加速圆周运动可以使载体在水平两方向有加速度变化,满足可观测性原则(2),所以设计的轨迹满足标定路径设计原则。
设定标定路径的运动参数如下。
静止时间10 s,拱桥半径为70 m,对应圆心角为60°,俯仰角频率为π/25,幅度为π/18,偏航角频率为π/25,幅度为π/2,加速度为2 m/s2,变加速运动时间为40 s,圆周运动的角加速度为0.1°/s2,圆周运动时间为80 s。
按式(4-31)建立状态空间模型,其中参数设置如下:
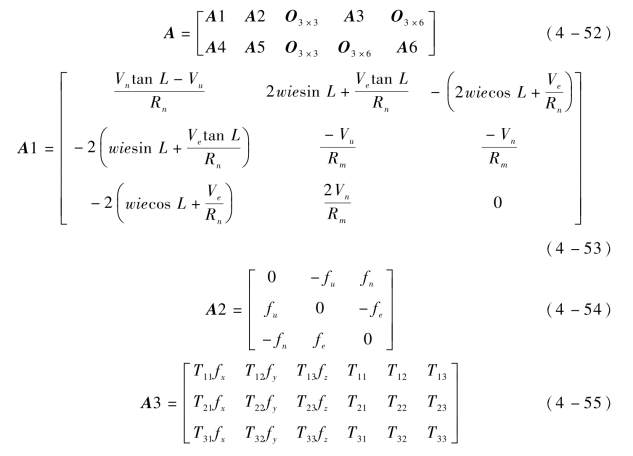

参照文献[68]将式(4-31)离散化以满足卡尔曼滤波要求,并设置滤波参数如下。
初始纬度为30°,经度为118°,加速度计刻度系数误差为10-3,常值偏置为10-3g,陀螺刻度系数误差为10-3,零偏为4×10-4rad/s,杆臂r取[232]m,子惯导安装误差角三轴向均设置为10′,状态变量X的初值都为0。
初始方差阵为
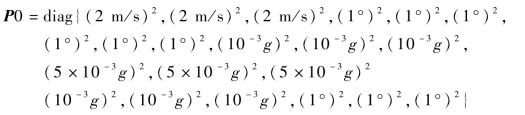
系统噪声协方差为
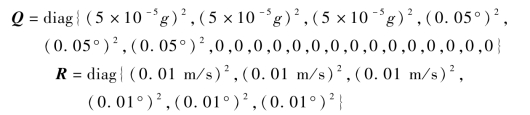
各误差估计结果如图4-2、图4-3所示。其中直线为设定值,曲线为估计结果。
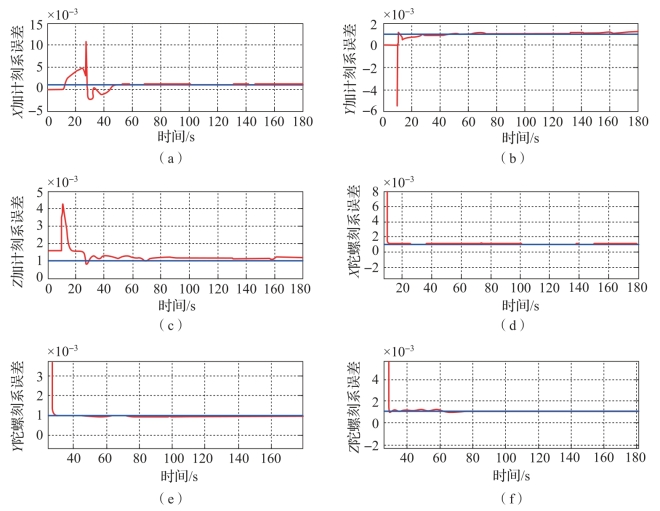
图4-2 刻度系数误差估计结果(书后附彩插)
(a)X加计刻系误差;(b)Y加计刻系误差;(c)Z加计刻系误差;
(d)X陀螺刻系误差;(e)Y陀螺刻系误差;(f)Z陀螺刻系误差
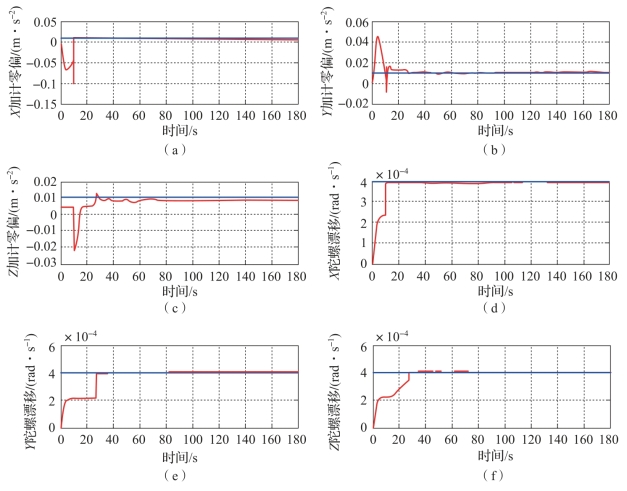
图4-3 加计零偏和陀螺漂移估计结果(书后附彩插)
(a)X加计零偏;(b)Y加计零偏;(c)Z加计零偏;
(d)X陀螺漂移;(e)Y陀螺漂移;(f)Z陀螺漂移
从图4-2和图4-3可以看出,经过一段时间的滤波,惯导12个误差参数都收敛到稳态值,但各个参数的收敛时间差别很大。这说明在所设定路径下,各参数的可观测度不同。下面就从可观测度的角度出发分析仿真结果,运用基于奇异值分解的PWCS可观测性分析方法进行分析,计算出每个奇异值所对应的状态变量,并画出各个状态量的直方图,如图4-4所示。
图4-4的横坐标表示各个状态变量,每个数字对应着一个状态变量,状态变量的排列顺序按照滤波器设计时的顺序排列,纵坐标表示幅值。从可观测度结果来看,各参数都可观测,状态变量对应的可观测度都大于0.9。从而说明了所设计路径的合理性。
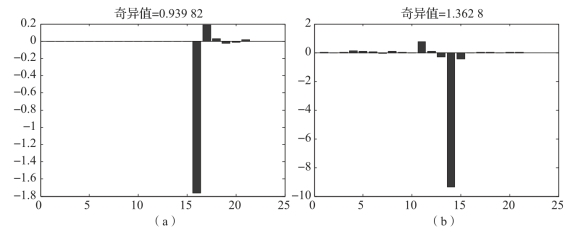
图4-4 各奇异值对应的状态直方图
(a)状态变量δVx的奇异值;(b)状态变量δVy的奇异值
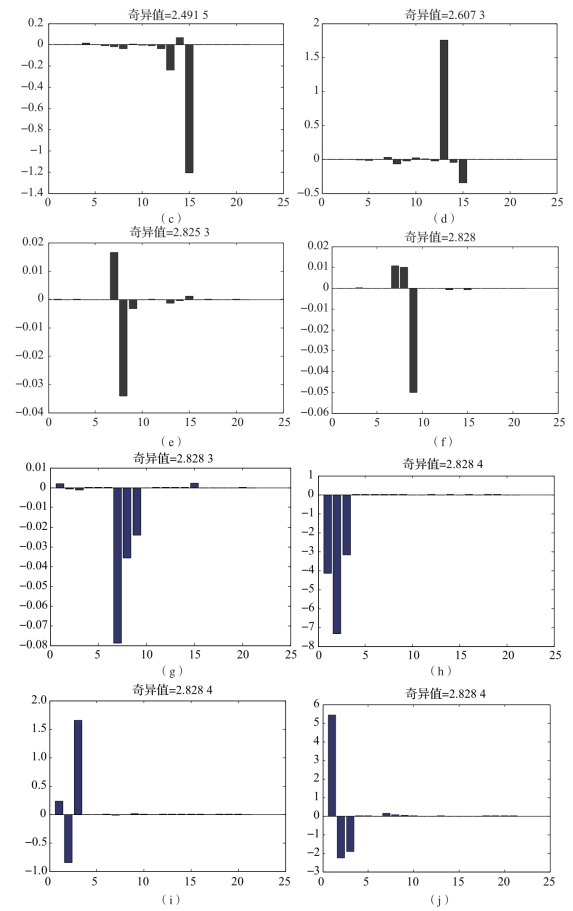
图4-4 各奇异值对应的状态直方图(续)(https://www.daowen.com)
(c)状态变量δVz的奇异值;(d)状态变量φx的奇异值;(e)状态变量φy的奇异值;
(f)状态变量φz的奇异值;(g)状态变量μx的奇异值;(h)状态变量μy的奇异值;
(i)状态变量μz的奇异值;(j)状态变量δKax的奇异值
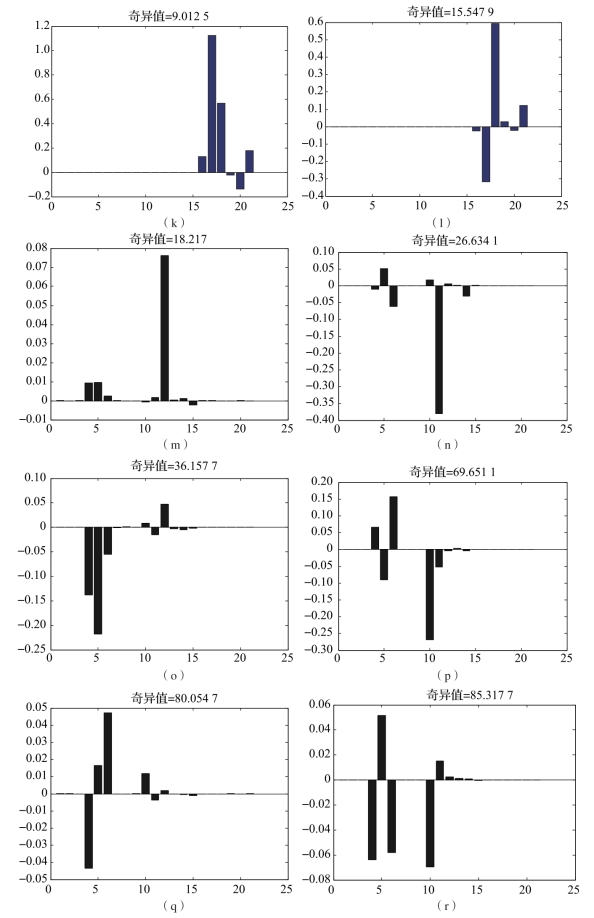
图4-4 各奇异值对应的状态直方图(续)
(k)状态变量δKay的奇异值;(l)状态变量δKaz的奇异值;(m)状态变量∇x的奇异值;
(n)状态变量∇y的奇异值;(o)状态变量∇z的奇异值;(p)状态变量δKgx的奇异值;
(q)状态变量δKgy的奇异值;(r)状态变量δKgz的奇异值
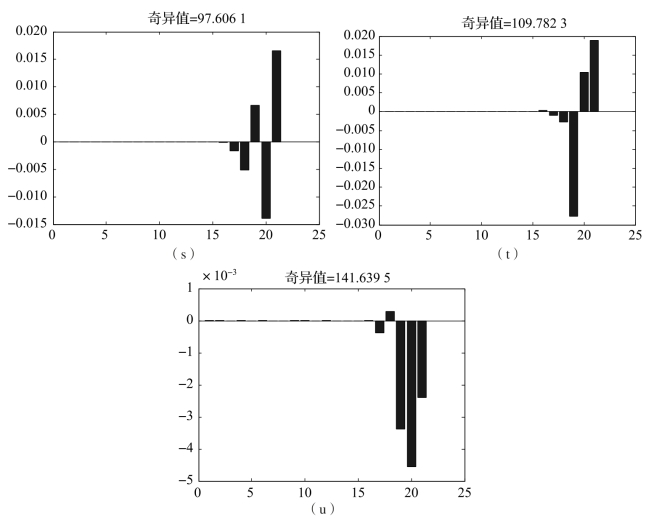
图4-4 各奇异值对应的状态直方图(续)
(s)状态变量εx的奇异值;(t)状态变量εy的奇异值;(u)状态变量εz的奇异值
收敛时间也是标定结果好坏的重要标志,各参数收敛时间统计结果如表4-1所示。
表4-1 各参数收敛时间统计结果
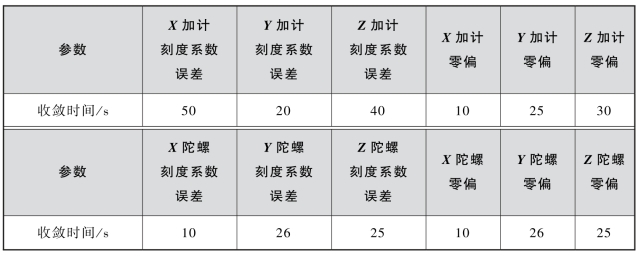
从表4-1可以看出各参数的收敛时间都较短,都能在50 s内达到稳态值。其中X加计刻度系数误差和Z加计刻度系数误差的收敛速度较慢。这也说明该路径适合在线标定的进行。
除了可观测度和收敛时间外,我们最关心的是标定的精度。对惯组各误差参数,取参数收敛后一段时间140~180 s的估计值的平均值来作为该次实验误差参数的估计值,考虑到惯性仪表随机噪声的影响,重复做上面仿真实验5次,取5次实验计算结果的平均值作为误差参数的估计值,并将估计值减去设定值,得到的结果除以设定值得到相对精度。其具体结果如表4-2所示。
表4-2 参数估计精度
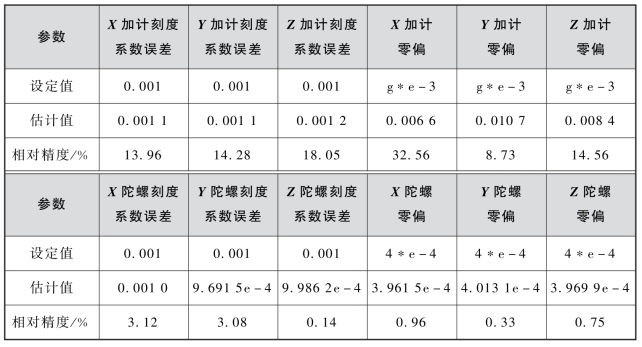
从估计精度来看,陀螺参数的估计精度较高,都能达到3.2%以内。而加速度计参数的估计精度相对较低,除X加计零偏的估计精度稍低外,其余参数都能达到19%以内。需要进一步研究内在机理以达到在最短的时间内获得最高的标定精度。
从可观测度、收敛时间和标定精度三方面的分析都说明本小节所设计路径的合理性。但具体参数的选择需要进一步优化以提高可观测度,缩短收敛时间和提高标定精度。
实际的炮车运动过程难以按规定的轨迹进行,为了进一步验证标定路径设计原则的正确性,改变运动轨迹的顺序后进行仿真。运动顺序改变为:炮车静止一段时间后,摇架在水平方向转动360°,然后加速运动,给予炮车一定的速度,炮车做变加速运动的同时摇架按正弦规律做俯仰和偏航角运动,一段时间后,以变角速度通过一座拱桥,接着炮车以变角加速度做圆周运动的同时摇架按正弦规律做俯仰和偏航角运动。仿真参数设置与本小节相同。在该路径下进行仿真,得到结果如图4-5和图4-6所示。
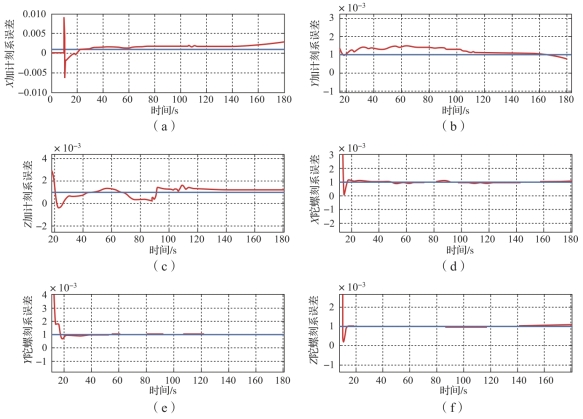
图4-5 改变机动顺序条件下刻度系数误差的估计结果(书后附彩插)
(a)X加计刻系误差;(b)Y加计刻系误差;(c)Z加计刻系误差;
(d)X陀螺刻系误差;(e)Y陀螺刻系误差;(f)Z陀螺刻系误差
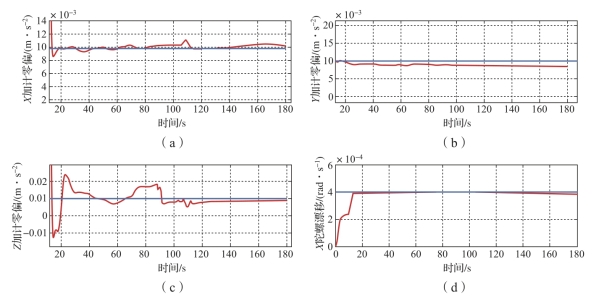
图4-6 改变机动顺序条件下陀螺漂移和加计零偏的估计结果(书后附彩插)
(a)X加计零偏;(b)Y加计零偏;(c)Z加计零偏;(d)X陀螺漂移
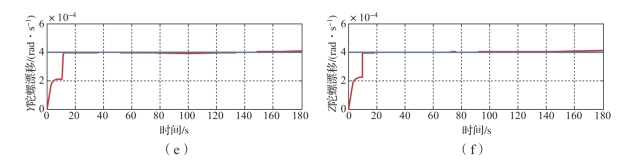
图4-6 改变机动顺序条件下陀螺漂移和加计零偏的估计结果(续)(书后附彩插)
(e)Y陀螺漂移;(f)Z陀螺漂移
从图4-5可以看出,改变机动顺序后,参数同样能得到估计。Z加计刻度系数和Z加计零偏的收敛速度变慢是因为所设计的路径中只有通过拱桥才能激励Z加计刻度系数和Z加计零偏。这说明误差激励与运动的先后顺序没有关系,从而验证了所提路径设计原则的合理性。
