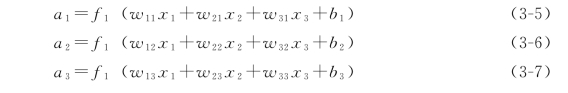眼底图像质量分析的主要组成
1.数据集
随着便携式眼底照相机的普及，人们可以得到大量的眼底图像。由于在图像的获取过程中存在光照不适、拍摄环境不佳、设备参数设置错误等客观因素及操作不当、医务人员经验不同、培训不统一、患者配合度不高等主观因素，数据库中的眼底图像质量不一。常用的公开眼底图像来自Kaggle竞赛官网的EyePACS公开数据集。Kaggle竞赛官网于2010年创建，为企业和数据科学家提供了一个平台。组织方或企业将数据和问题发布到Kaggle竞赛官网上，相关的数据科学家和科研人员会为问题提供相应的解决方案。其中的竞赛涉及众多领域。2015年，Kaggle竞赛官网发布了糖尿病视网膜病变检测的赛题，提供了包含80 000多张视网膜眼底图像的EyePACS公开数据集，其中有30 000多张为训练集，其余为测试集。这些图像于不同国家地区采集，用于采集的眼底照相机型号和参数也各不相同，图像和图像之间在色彩和光照上存在较大差异。图像的尺寸分辨率最小为2 592×1 994，最大为4 752×3 168。此外，该数据集也包含不同种族的眼底图像。该数据集的数量虽然巨大，但其中存在大量不可用于诊断分析的眼底图，这些图像的质量在医学上是不可接受的，其中质量差的眼底图像可能存在光照不足、曝光过度、遮挡、模糊等多种问题。
2.卷积神经网络
卷积神经网络（CNN）是眼底图像质量分析的人工智能算法的核心组成部分，其基本结构包括卷积层、池化层、激活层、全连接层等。
卷积层广泛用于深度神经网络样本特征的获取。在卷积层中，通过一个指定尺寸的窗口卷积核对整幅图片进行扫描，从而提取出更高级的特征。通过设置卷积核的步长来限定窗口每次滑动的像素个数。对于处于边界上的像素，在做卷积操作时可以选择是否对其进行填充。卷积层的输出结果可由公式（3-1）获得。
式（3-1）中，
代表第l层卷积神经网络中第n个特征图的输出值，
用来表示卷积核的参数，
为偏置项，
表示该层特征图的输入集合。f（·）为激活函数，f（·）的选取通常有以下几种。
Sigmoid函数，函数表达式如公式（3-2）所示。它是一种非线性的激活函数，其取值范围为[0，1]。输入的值越小，输出越接近于0，反之输入的值越大，输出越接近于1。使用Sigmoid函数作为激活函数容易导致梯度弥散。此外，由于Sigmoid函数的输出恒大于0，这会导致收敛过慢，增加训练网络模型的时间成本。
双曲正切函数tanh，函数表达式如公式（3-3）所示。tanh函数是Sigmoid函数的一种变体，相比于Sigmoid函数，其取值范围为[－1，1]。输出为零中心数据。
ReLU激活函数，函数表达式如公式（3-4）所示。ReLU函数对于输入值小于零的值进行抑制，只保留输入值大于零的值，具有稀疏激活性的特点，可以避免反向传播的过程中梯度消失，很大程度上提高了网络训练的速度。此外，ReLU函数的效率要比tanh函数和Sigmoid函数高，能够快速收敛。除了ReLU函数之外，还有在ReLU基础上的改进函数如Leaky-Re LU、R-Re LU。由于Re LU函数中小于0的输入全部输出为零，这将导致深度神经网络中的某些神经元不会被激活。如果学习率比较大，这些神经元可能一直输出值都为0。为此，Leaky-Re LU保留了负轴的值，这些值比较小，但不会丢失全部信息。
池化层作为卷积神经网络的重要组成部分，可以通过池化操作对数据进行压缩，大大减少了参数的计算量。与卷积核类似，池化层也需要一个滑动的窗口，可以定义步长和池化的方式，以及是否对边界进行填充。区别在于，池化层的窗口只影响输入的一个深度，而卷积层的过滤器横跨了整个深度。当处理大幅图像时，在一个区域卷积后得到的特征很有可能在其他的区域也具有类似的特征。对于图像特征的提取，通过池化操作计算图像上某个区域特征的平均值、最小值或者最大值。这样得到的统计特征和使用卷积层输出的所有特征相比，数据维度更低，解决了过拟合的问题，对网络性能有较大改善，常用的池化方式有以下2种。
（1）平均池化。其池化的方式是通过滑动窗口框出用于池化操作的子区域，然后对其中的值加和取平均，作为输出结果。平均池化的操作过程见图3-1。
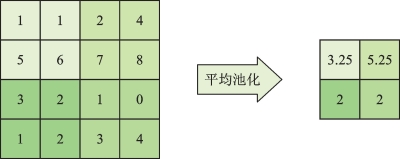
图3-1 平均池化操作过程
（2）最大池化。其池化步长和池化窗口与平均池化相同。框出子区域后，选取其中特征子区域的最大值作为输出结果。最大池化的操作过程见图3-2。
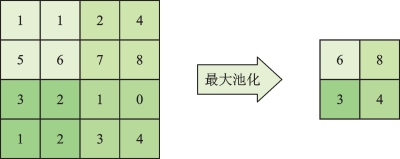
图3-2 最大池化操作过程
全连接层可以对池化层和卷积层输出的特征进行压缩，同时完成模型分类。在全连接层中，每一层神经元的节点都与上一层所有神经元结点相连接，所以称为全连接层。其结构见图3-3。
令x1、x2和x3为该网络的输入值，a1、a2和a3为全连接层的输出值，我们用wih表示两个全连接层之间的连接权重，bh代表全连接层神经元的偏置，激活函数用f1（·）表示，则输出a1、a2和a3分别如公式（3-5）（3-6）（3-7）所示。
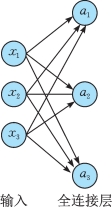
图3-3 全连接层示意图
