老娘舅分家
有个阿拉伯财主死了，生前立下遗嘱：“有11匹好马留给三个儿子，老大得
，老二得
，老三得
。”
三兄弟没有办法分，只好请舅舅做主。后者足智多谋，远近闻名。他二话没说，就把自己的一匹千里马牵了来，与姐夫的11匹马加在一起，凑成12匹。这样一来就好分了：老大6匹，老二3匹，老三2匹，三个儿子正好把老父留下的11匹马分完，舅舅的千里马仍旧物归原主。儿子们请舅舅吃饭，坐在庆功宴的首席。
又有法国的一个守财奴，死后要把13粒价值连城的钻石留给三位千金：大姐应得
，二姐应得
，三妹应得
。由于13是个奇数，而钻石若被切割必将大大贬值，没法分配，只得请教舅舅。舅父一听，就说：“好吧！我替你们做主，先拿掉1粒钻石作为我的‘劳务费’吧。”三姐妹欣然同意，剩下12粒，当然好分得很。按照规定比例，大姐拿走6粒，二姐拿走4粒，三妹应该拿3粒。可是台面上只剩下2粒了，老三一看就哭鼻子。这时舅舅说：“这样吧，我的劳务费不要了，仍旧还给你！”于是老三破涕为笑。大家拿出钱来，在大酒店设宴招待舅舅，尽欢而散。
为什么两个民族的两位老娘舅做法如此不同呢？不难看出，关键在于儿子们的分配比的和
，而女儿们的分配比的和
。都是以12作为中间数，一个稍大些，一个稍小些，都不是1。
我们知道，马和钻石是不能分割的，但土地则不然。假定老头子的遗产不是马而是11亩土地，那就不必劳舅舅的大驾了。
大儿子第一次就可以分到
老二分到
老三分到
当然，11亩田并不能正好分光，还剩下
亩。
按比例再分，大儿子在第二次又能分到
（亩），老二、老三也都各有所获。可是仍未分完，还剩下
亩土地待分配。
第三次分过以后，老大又能分到
（亩），老二、老三也各有所获，最后仍然剩下少量土地要待分配。就这样一直分下去，直到最后微乎其微，连一只脚指头都容纳不下时，就可以忽略不计了。
不难算出，老大能分到的田亩数为：
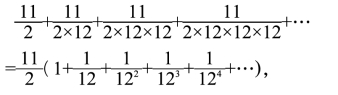
括弧里头是一个无穷递降等比数列，根据求和公式可以算出，它的极限是
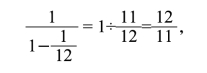
所以老大能分到的最终田亩数为：
类似地，可以算出老二能分到3亩，老三能分到2亩。你看，这些数目竟同老娘舅建议的分法不谋而合！
这就是用“极限”的观点来看待分割遗产这个问题。你们看，数学多么有趣啊！