一道香港数学竞赛题
有些数学题很难解，做这种题目只能让人伤脑筋，并没有什么实际意义。还有一种题目，它可以吸引你废寝忘食地去解开它，我们称它为“好题目”。显然，“难题目”并不等于“好题目”。
现在社会上有很多面向中、小学生的数学竞赛，竞赛题一般都很难，但是称得上“好题目”的却不多。难怪有一位著名的数学教育家感慨地说：“我们应该从香港的小学数学竞赛中得到启示。反思我们搞的比赛，有些小学生竞赛题连大学教师都做不出，还得专门聘请大学数学系的教授来培训小学生，真是劳民伤财！”
确实，香港数学邀请赛的竞赛题难度适中，甚至偏易，联系生活中的问题，趣味盎然，不是少数几个人闭门造车的虚构产品。你不信吗？请看下面这个例子。
在某年的某一个月中，星期六和星期天的日数相同，有三个星期天都是奇数日子。试问：这个月的8日是星期几？
刚拿到这道题目，难免有“丈二和尚摸不到头脑”的感觉。但只要你是个有好奇心的人，不管男女老少，都会被它打动，试着来解开它的谜底。之所以说它有吸引力，道理就在这里。
解开这道题目，并不需要“脑筋急转弯”。大家知道，一星期有七天，凡是两个连续的星期天，必然有一个是奇数日子，另一个是偶数日子。题目中既然说，这个月份的三个星期天是奇数日子，聪明的你马上就会想到：这个月肯定有五个星期天（三奇二偶）。为了迅速找到答案，最好的办法就是画出一张月历，（表一）就是一种可能的方案。
表一
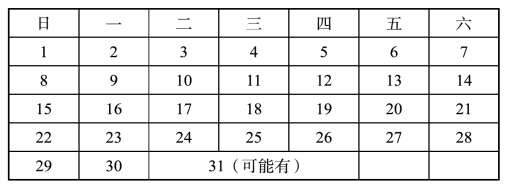
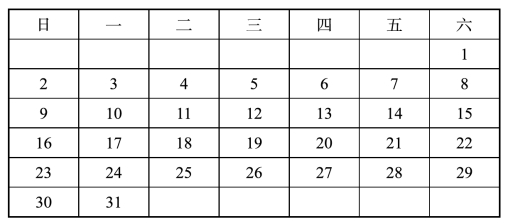
但是这张日历只有四个星期六，违反了题意“星期六和星期天的日数相同”。不过，我们已经找到解题的钥匙，只要对日历加以调整就行了。如果把该月的1日调整为星期六，那样一来，星期六和星期日的天数就相等了。然而，奇数日子的星期天只有两天而不是三天（表二），还是不合题意。
表二
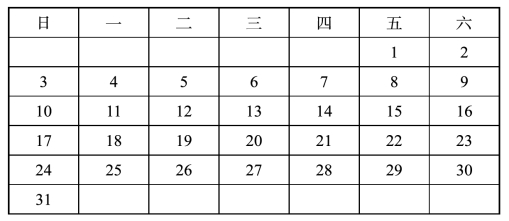
于是，我们只剩下最后一种方案（表三），它符合了题目的全部要求。如果你手头正好有一张2004年的日历，可以迅速地进行核对，并立即找到答案——该年的10月份，8日是星期五。
表三
通过解这道题目，我们至少得到两点教益：
第一，假设和调整，是解决许多难题（不能说一切难题，但肯定是其中的大多数）的法宝。
第二，通过逐步修正，可以使假的尽去，逼出真的。