玩弄数字的奇人
人的大脑蕴含着很大的潜能，尚未得到充分开发，譬如说，有人拥有与生俱来的、惊人的速算天赋，有人则通过艰苦自学而掌握了不传之秘。究竟怎样看待这类问题，学者们意见分歧，存在着很大的争议。
有人坦率地谈了几点看法：一、不应该提倡，也不必大肆宣扬，因为毕竟不是数学的主流；二、大部分人是学不来、做不到的，道理很简单：你不可能希望人人都成为百米飞人或者跳水冠军嘛！但也有人认为，速算里头可能潜伏着某些秘密和窍门，把它们揭露出来，肯定有助于数学及其相邻学科的发展。
我国的邻邦印度曾经出过一位速算巨星沙昆塔拉。这位家境贫寒、原来文化水平也不高的妇女具有一种非凡本领，开23次方结果可以准确到个位数，速度超过计算机。消息不胫而走，许多国家都重金邀请她去当众表演，既算游戏，也算魔术。于是她挣得不少酬金，着实发了笔不大不小的财。拿印度的标准来说，也算得上一个“富婆”了。然而，当人们请教她究竟用什么秘诀才能做到这一点时，她却守口如瓶，不肯吐露半字。
英国剑桥大学的名誉教授露斯鲍尔，在其跨世纪的名著《数学集锦》中不无惋惜地说过，历史上几乎所有的速算天才都把他得来不易的独特技能居为奇货，当成不传之秘而带进了棺材，未免太可惜了。
我国已故著名数学家华罗庚先生独具慧眼，他在生前曾对沙昆塔拉的开23次方进行过一番探究。这个难题在华先生智慧炮弹的重重轰击下终于露出了一丝曙光，发现其中确实存在着一些诀窍。至于华先生所获的成果是否就是沙昆塔拉本人所掌握的办法，那当然是无法加以对证的。
另有一些研究家则认为，关键是“硬件”而非“软件”。他们猜想速算奇人的大脑机制与一般“凡夫俗子”的大不相同，具有“多通道”平行处理信息的能力。纵然他们自己愿意把这种非凡本领传授于人，别人也学不会。
上述说法是否过甚其词？这里不妨引一个有名的故事。印度天才数学家拉马努贾对数字特别敏感，近乎“条件反射”，连他的老师、数论专家哈代也望尘莫及。有一天他和哈代一起出门去，叫到一辆牌照为1729的出租汽车。哈代认为，“这可是个一点儿也没有趣味的数”。岂知拉马努贾马上反驳：“不！它有两种不同办法可表为两个数的立方和，即
1729=1000+729=103+93；
1729=1728+1=123+13。”
别人不相信，仔细一算，果然毫厘不差，令人十分佩服。
正是出于这种对数字的敏感性，速算奇才们有时可以做出令人目瞪口呆的即兴表演。让我们来看一则“数字通灵术”的现场表演吧。
试问：
4109589041096×83=？
看上去，83是一个平淡无奇、毫无特征的“素数”。所以一般人看来，那个长达13位的因数，用83去乘，算起来总不会轻松的。岂知，有位速算巨星竟在不到几秒钟的时间内完成了这个乘法。听起来，这不像是神话吗？此人岂不是与能吞吃玻璃的奇人有异曲同工之妙，甚至比他更为神奇？
其实，他根本不去执行乘法，而是把3和8拆开来，分别放在第一个因数的前面和后面，其他数字则纹丝不动。就这样，一下子便得出乘积341095890410968，完成了“闪电乘法”。
如果你信手写出一个数，用83来乘，是否可以照搬这种办法呢？那当然是不行的！
速算天才的本领，就在于他与一般人不同，领悟到83与4109589041096乃是一对关系特殊、形影不离的“共生数”。
一枝红杏，泄露春光；共生数的露头激起了人们的极大兴趣，纷纷起来刨根寻底。经过一番探索，终于发现道理倒也并不复杂。一经点破，即使只有中学程度的人也都能理解。
如果一个n位数x与83的乘积有上述奇妙性质，那么可以通过方程来表示：
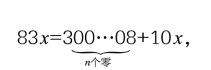
移项以后，即可化简为
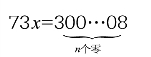
这就是说，如果73能够整除一个以3打头，以8结尾，中间夹着一系列零的数，那么这个商数就是符合条件的x。
让我们通过竖式除法来算算：
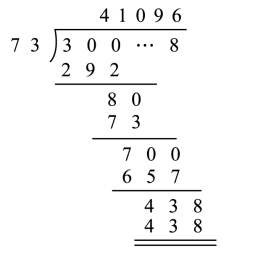
所以41096就是符合条件、可以做游戏的一个候补对象。
接着再往下讲，道理就隐晦而深刻得多。在做除法时，如果我们偶尔疏忽，没有及时把末位的8用上，那么除法是否没完没了地一直做下去？也不见得！
这是由于
是一个循环节只有8位的循环小数，所以当初如果一时大意而错过了除尽的时机，那么你也不要担心，顶多再除8位，机会就会再次出现！
就这样，我们得到了与83配对共生的第二个候补对象41095/8904/1096。它就是题目一开始就出现的、长达13位的天文数字。
到此地步，也许你已经明白，只要在前面不断添加一节41095890的8位数，最后加上永恒的尾巴41096，就能得出位数越来越多、无穷无尽的“共生数”。
人们当然会提出问题，除了83之外，是否还有别的两位数也具有如此这般一前一后、“闪电乘法”的性质呢？
答案是：当然有啊，所用方法与本文所说的大致差不多。读者们不妨自己去搜索一番，做起游戏来才会格外有趣。