一个数据订合同
上海苏州河边的一家废旧厂房，被私人企业家马先生承包了，生意做得很红火。
不久前，装潢公司收到马先生来信，附来一张图纸，要求订立供货合同，计算工程费用。马老板在信中说，他打算专门划出一个区域，改建为一个环形画廊，向海内外收藏家征集展品，其中不仅有名家油画，还有钻石、珠宝、琉璃、鼻烟壶、金铜佛像等。
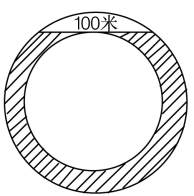
装潢公司的业务经理看到设计图（左图），不禁冒起火来。原来，图中只有一个数据——标出的尺寸是与内圆相切的弦长为100米。不知道圆环的面积，就无法得知要用多少地毯，至于工价，那更是无从谈起了。业务经理心想：马老板真是个十足的马大哈，难怪他要姓马了。
业务经理的想法错了，马先生虽然姓马，，却不是一个马大哈。其实，图上虽然只有一个数据，信息量已经足够了。
有人用“量变到质变”的观点解释给他听：圆环的面积是外圆与内圆的面积之差；倘若内、外两圆同时缩小，使它们的圆半径之差保持不变，那么，当内圆的半径减小到0时，圆环就不成其为圆环，变成一个圆了，而此时的直径正好是弦长100米。所以，它的面积等于π×（
）2，也就是大约7854平方米（此处取π的近似值为3.1416）。用做画廊，这样的面积不大不小，非常合适。
不料业务经理听了这样的解释之后，还是似懂非懂。他坚持说：“我听不懂，也理解不了。我需要的是一种‘静态’的解释，否则，合同不能订！”
别急，别急！你要“静态”解释吗？这又有何难。让我来说给你听一听。
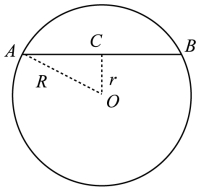
“如右图，设大圆半径为R，小圆半径为r，C是弦AB的中点，O为外圆与内圆的公共圆心，那么OC⊥AB、△OAC当然是直角三角形啰。根据勾股定理，R2-r2不就等于AC2吗？
“而圆环的面积正好就是兀（R2-r2）=π×（
）2，请看，一个数据不是完全足够了吗？”
业务经理听了，恍然大悟，欢欢喜喜地签了合同。通过这个教训，他深感自己的几何知识严重不足，决心今后要好好补习，以使自己在今后的生存竞争中不处于下风。