答案与提示
第七副面孔
根据这6副面孔，我们可以分析出它们存在以下3种模式：
第一种模式是面孔的轮廓。它们依次为圆、三角形和倒放的三角形，所以，我们可推出第七副面孔的轮廓一定是一个圆。
第二种模式是面孔中的眼、鼻、口的形状。第一副面孔眼、鼻、口的形状都是圆或弧形的，但在第三副面孔中，嘴巴变为夹角形状。而到了第五副面孔，嘴巴与鼻子都变成夹角形状。所以，我们由此推想，到了第七副面孔，除了嘴巴与鼻子变成夹角形状外，眼睛也应变成夹角形状。这个推想还可从第二、四、六3副面孔中的眼、鼻、口的变化得到证实。
第三种模式则是面部的表情：笑眯眯与愁眉苦脸交替出现。因此，第七副面孔一定是笑脸。
渔夫分鱼
先算一算总数。7筐是装满鱼的，还有7筐只装半筐，所以一共有7×1+7×
=10.5（筐）。很明显，10.5÷3=3.5（筐），所以每人应分到3.5筐鱼。我们稍微想一想，就能得出两种解法了：
第一种分法：
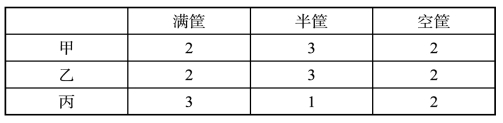
第二种分法：
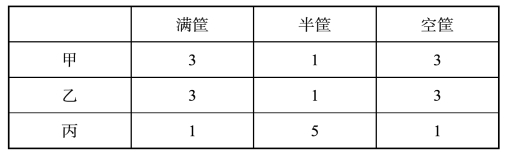
请看，不但鱼分得绝对平均，甚至连装鱼的筐子也分得“一碗水端平”——大家都是7筐。
找出标准答案
题目已知，3个人都答对了5题。我们可以两两进行比较。对任何两个人来说，尽管他们俩答对的题号不见得全部相同，但至少有相同的3道题是大家都答对的。
从题目上的表格可知，对于第二，四，五题，甲、乙两人都答对了；对第一，五，六题，乙、丙两人都是答对的；对第三，五，七题，甲、丙两人都是答对的。所以正确答案即可得出：
3只砝码称东西
使你吃惊的是，从1克到13克的东西都可以称。
让我们把各种情况列举如下：
（1）只使用一只砝码时，可称的重量为1克、3克、9克。
（2）使用两只砝码（在同一盘上）时，可称的重量为4克、10克、12克。
（3）使用三只砝码（在同一盘上）时，可称的重量为13克。
（4）同时使用两只砝码（分别位于两只盘上）时，可称的重量为2克、6克、8克。
（5）同时使用三只砝码（分别位于两只盘上）时，可称的重量为5克、7克、11克。
题目已经做完了，但还有一些话要讲，而且可以说，这些话比解题本身还重要。
这道题目显然是从古老的题目——用1克、2克、4克三种砝码可以在天平上称出几种不同重量的东西——变化出来的。使我们惊奇的是，那道题目的答案是从1克到7克的东西都可以称。
当然，从1、2、4三种砝码改变为1、3、9三种砝码，是一种明显的进步。因为前者只能称7种重量，而后者却可以称13种重量。能不能再改进呢？由于
1=20，2=21，4=22，
1=30，3=31，9=32，
这就启发我们，能不能改用1克、4克和16克这三种砝码，以进一步扩大称量范围呢？
什么事情都不能想当然。如果采用1、4、16克这三种砝码，那么2克的东西就称不出来！还有6克、7克等等也都不行。因为用这三种砝码中间出现了许许多多的“漏洞”。这种所谓的“砝码”，我们自然不屑一顾。
从这种意义来看，用三种砝码称东西，最好的办法就是使用1克、3克和9克。这已经是“好到了顶”的办法。
汉斯和卡丽娜的难题
解这个难题时，不能掉以轻心，必须考虑到牧草每天的生长量。要注意的是，如果说牛与山羊一起吃可吃45天，那它们把在此期间新长出来的牧草也吃光了。由于牛的食草量等于鹅与山羊的食草量之和，所以，牛与羊一起吃草的食用量相当于2只山羊与1只鹅在一起吃的食用量。由于1只山羊与1只鹅在一起可以吃90天，正好相当于2只山羊与1只鹅在一起吃的时间（45天）的2倍，于是，我们不妨认为原有的牧草量可供1只山羊吃90天，而鹅是专门吃新长出来的草。这样，我们就可假设牛每天吃的草为原牧草量的
，羊每天吃
，那么羊和牛在一起吃就是每天吃
。所以，牛、羊、鹅一起吃，可维持36天。
本题解法的玄妙之处，就在于把牛与山羊看作专吃牧场里原来的牧草，而鹅则专吃新长出来的牧草。于是，本问题得到圆满解决。
巧分玉佩
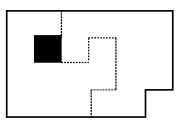
分割办法如右图所示，说难也不难。可以你们核算一下，每块玉佩的面积都是11平方厘米。由于厚度均匀，所以两块玉佩的分量是完全相等的。它们的形状像是左右手对称；在空间翻一个身，就完全重合了。这些你们都不难用廉价的方格纸来实地试一下。
趋吉避凶
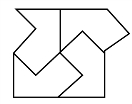
分割办法如左图所示。请注意在分割之后，每位兄弟所拿到的玉器挂件，仍是一边凹进去一块，另一边凸出来一块，但其凹相位却是相差90°；而且，伯爵原来的传家宝是八边形，4兄弟所拿到的东西，却成了六边形了。
巧摆花瓶
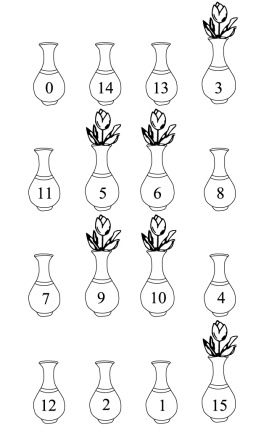
这则动脑筋题的答案如下图所示。横4行、竖4列及两条对角线上的数字之和为30。按题目要求，在移动过程中有7个瓶子（见图中插花的及8号瓶子）没有移动，仔细一看还可发现，只有一只8号瓶的位置确确实实没有移动过。
车窗照面
也许你会说，快车速度V1慢车速度V2都不知道，没有速度这个重要数据，问题怎么能解决呢？这不要紧，因为可按相对运动的原理进行分析。设想自己坐的列车不动，而对方所在的火车以V1+V2的速度驶来。请注意，这个V1+V2的速度无论对快车上的小红还是慢车上的小明都是一样的——这是解决本题的关键。
这是一个典型的正比关系问题，列出比例式：
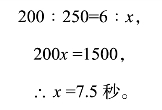
因此，小红看见整列慢车驶过窗口所用的时间是7秒半。
有意思的是，火车驶过窗口所需的时间主要取决于列车的长度，而不论它是快车还是慢车。因此，如果快车挂的车厢多，车身长，那么它驶过窗口所用的时间比慢车驶过窗口所用的时间多。
两只蟑螂
咪咪的走法是一条回路（见下页图），它把立方体的6个面都“扫描”到了。读者们，你们自己不妨用硬纸做一个简单模型试一试，便会恍然大悟。
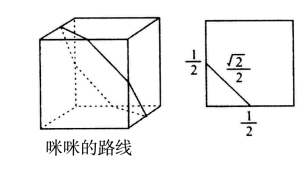
容易看出，这条路线由6段组成，每段的长度是
，因此总长度等于
（厘米）
至于底底的路线呢，则再妙不过。它由3段组成，每段的长度是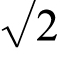
，所以总长度也是3
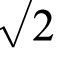（厘米）。两者半斤八两，平分秋色。
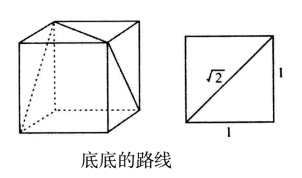
人们自然要问：底底这种走法，能满足预定要求吗？请注意，立方体的每个角，恰好是3条棱的交会点。所以，这样走，12条棱边全都触及到了，满足了底底“每条棱至少都咬一口”的要求。
有情人终成眷属
原来，安东尼奥注意到，写在金盒子铭牌上的话与写在铅盒子铭牌上的话是互相矛盾的，因此这两句话中必有一句真话，一句假话。至于何者为真，何者为假，他用不着再去考究。既然真话只有一句，那它显然已经用掉了，因此写在银盒子铭牌上的话肯定是句假话。既然这句话说的是“肖像不在这只盒子里”，而它是句假话，可见肖像倒确实是放在银盒子里的呢！
顺便说一句，在莎翁原著中，她的肖像是放在铅盒子里的。在安东尼奥正式猜谜前，她先唱了一首歌，以便给他暗示，其中有句歌词是：
告诉我爱情生长在何方？
它是在脑海，还是在心房？
本题的改编者是著名数学科普大师马丁·加德纳先生。
林之洋斗智两面国
牛头、马面的话可真可假，非真即假。林之洋做了下面的分析：
如果牛头的这句话是真话，那么他是在星期四说的；如果这句话是假话，那他就是在星期一说的。因此，牛头说这句话的可能日子不是星期一，就是星期四。
如果马面的这句话是真话，那么他是在星期日说的；如果这句话是假话，那他就是在星期四说的。因此，马面说这句话的可能日子不是星期日，就是星期四。
所以，林之洋断定这天是星期四。这种推理法，和几何学里的“轨迹相交法”有异曲同工之妙。
张冠李戴
为了简洁起见，我们用A、B、C、D表示参加舞会又演出这幕“喜剧”的4个男青年，用小写字母a、b、c、d表示他们自己的帽子。
有了“人”和“物”两个要素，我们就可以造一张表格。
题目已告诉我们：A和B虽相互攻击，可实际上A并没有拿b，B也没有拿a。于是，A拿的只可能是c或d，B拿的也只能是c或d。
因为不可能同时出现两个c或两个d，所以有两种可能性：
（1）
（2）
这两张表格暂时还不完整，需要我们根据题目里头的其他线索加以补充。
先填第一张表。题目中的条件说“C拿了一个人的帽子，但这个人并没有拿C的帽子”，由此可见，C的下面一定不是a，因为A已经拿了c，所以C的下面只能是b。于是，D的下面非填a不可了。这时，表格（1）已经填完：
（1）
但是，题目中的条件明明告诉我们，D拿了一个人的帽子（从表中来看，此人应是A），这个人把错拿了A的帽子的那个人（从表中来看，错拿了a的人是D）的帽子拿走了。也就是说，A拿到的帽子应是d，但表中却是c，可见这张表是错误的。
于是，我们只能按照同样的方法来填表格（2）：
（2）
大家可以检查检查，这张表满足题目中的一切条件，丝毫不存在矛盾。从表中可以看出：C拿的是A的帽子，B是最先离开舞场的。
交换火花
这个问题如果没有一种有效的思考推理方法，势必搞得像一团乱麻。
有个聪明人是这样考虑问题的：第一个把12个城市的火花全部收集齐全的人肯定至少要收到11封信，即除了他本人以外，居住外地的其他11位朋友都给他写了一封信，把他们各自住地的火花寄给了他。至于其他11个人呢，他们原先只有自己所住城市的火花票。因此，为了收集到全部12个地方的火花，每人最小限度要从别人那里收到一封信（在这封信里有他缺少的所有火花票）。
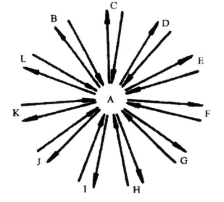
经过上述分析，于是他想到了一个巧妙的办法：先叫B、C、D、E、F、…、L这11个地方的收藏家各人准备一个大信封，把自己所在地生产的火花收齐11份，用挂号信寄给A。A在收齐各地寄来的挂号信之前，暂时按兵不动（这一点非常关键，A若急躁冒进，必然会使来往信件数增多）。
A收到各地寄给他的火花后，从每封信中抽出一套来，连同他自己所在城市产的火花，他就全部收集了。然后，A准备好A地生产的11份火花，接连发出11封信，分别寄给11位朋友，把除了收信人本地已有的火花之外的其余11份火花悉数寄去。于是，大家都如愿以偿，皆大欢喜。
综上所述，可知为了满足要求，至少要寄22封信（见上图）。由图可见，A好比是一个“工头”或“蜂王”，B、C、D、…、L等是普通“工人”或“工蜂”，他们只和A交换信息，彼此之间互不通气。
看来，这个问题虽小，却充满着浓郁的逻辑味道。